GPU Gems 2

GPU Gems 2 is now available, right here, online. You can purchase a beautifully printed version of this book, and others in the series, at a 30% discount courtesy of InformIT and Addison-Wesley.

The CD content, including demos and content, is available on the web and for download.

Chapter 41. Deferred Filtering: Rendering from Difficult Data Formats

Joe Kniss
University of Utah

Aaron Lefohn
University of California, Davis

Nathaniel Fout
University of California, Davis

In this chapter, we describe a toolkit of tricks for interactively rendering 2D and 3D data sets that are stored in difficult formats. These data formats are common in GPGPU computations and when volume rendering from compressed data. GPGPU examples include the "flat 3D textures" used for cloud and fire simulations and the sparse formats used for implicit surface deformations. These applications use complex data formats to optimize for efficient GPU computation rather than for efficient rendering. However, such nonstandard and difficult data formats do not easily fit into standard rendering pipelines, especially those that require texture filtering. This chapter introduces deferred filtering and other tips and tricks required to efficiently render high-quality images from these complex custom data formats.

41.1 Introduction

The key concept for achieving filtered, interactive rendering from difficult data formats is deferred filtering. Deferred filtering is a two-pass rendering approach that first reconstructs a subset of the data into conventional 2D textures. A second pass uses the hardware's native interpolation to create high-quality, filtered renderings of 2D or 3D data. The algorithm is incremental, such that rendering 3D data sets requires approximately the same amount of memory as rendering 2D data.

The deferred filtering approach is relevant to GPGPU computations that simulate or compress 2D and 3D effects using a difficult or nonstandard memory layout, as well as volume renderers that use compressed data formats. Relevant GPGPU applications include sparse computations and flat 3D textures (see Chapter 33, "Implementing Efficient Parallel Data Structures on GPUs"). Traditionally, high-quality rendering of these data sets requires that interpolation be done "by hand" in a fragment program, which in turn requires the reconstruction of multiple neighboring data samples. This approach leads to an enormous amount of redundant work.

Deferred filtering was first described in Lefohn et al. 2004. The paper presents algorithms for interactively computing and rendering deformable implicit surfaces. The data are represented in a sparse tiled format, and deferred filtering is a key component of the interactive volume rendering pipeline described in the paper. In this chapter we expand and generalize their description of the technique.

41.2 Why Defer?

Let's examine a simple scenario: imagine that you are rendering a volumetric effect such as a cloud or an explosion, and the 3D data have been compressed using vector quantization (see Schneider and Westermann 2003). This scheme compresses blocks of data by using a single value, called the key. The key value is used as an index into a code book, which allows blocks of data with similar characteristics to share the same memory. Reconstructing these data requires you first to read from the key texture, and then to read from the corresponding texel in the code book texture. Let's imagine that it takes four fragment program instructions to reconstruct a single texel.

One problem with this approach is that you cannot simply enable linear texture interpolation on the GPU and expect a smoothly filtered texture. Instead, linear interpolation must be implemented "by hand" as part of your fragment program. In practice, this is so expensive that renderers often resort to nearest-neighbor sampling only and forgo filtering completely. See Figure 41-1, top right. To perform "by-hand" filtering means we must reconstruct the 8 nearest texels and then perform 7 linear interpolations (LERPs) to get just a single trilinearly filtered value for each rendered fragment. Let's say that the original data size is 128³ voxels, the rendering fills a viewport of size 256² (that is, the rendering magnifies the data by 2x), and we are sampling the data twice per voxel. The number of fragments rendered would be 256 x 256 x 128 x 2, which totals approximately 16 million fragments. Now let's look at the number of fragment program instructions per fragment: 8 x 4 (8 texels times 4 instructions for each reconstruction) + 8 (texture reads) + 14 (for trilinear interpolation; LERP and ADD), which equals 54 instructions per filtered texture read. This brings us to a grand total of one billion fragment instructions for this simple rendering. As you can imagine, this might put a damper on your application's interactivity.

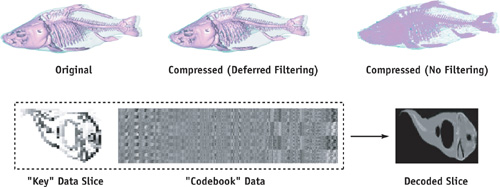
Figure 41-1 Vector Quantization Compressed 3D Data

41.3 Deferred Filtering Algorithm

To combat the explosion of fragment instructions required for texture filtering in the previous example, we advocate a two-pass rendering approach. This two-pass approach avoids redundant work (texture reads and math) and leverages the hardware's native filtering capabilities. The first pass reconstructs a local subset of the data at its native resolution, and the second pass renders the reconstructed data using the GPU's hardware filtering capabilities.

In the previous example, we described naive slice-based volume rendering (see Ikits et al. 2004) of 3D data stored in a custom, compressed memory format. Deferring the filtering to another pass has huge advantages, but it requires us to solve the problem slightly differently. Instead of rendering the volume by using arbitrary slice planes, we use axis-aligned slicing (utilizing 2D textures). This method renders the volume slices along the major volume axis that most closely aligns with the view direction. Just like Rezk et al. (2000), we generate trilinearly filtered samples between volume slices by reading from two adjacent 2D slices and computing the final LERP in a fragment program.

Figure 41-2 depicts the process. The algorithm proceeds as follows (note that steps A and B in the algorithm correspond to steps A and B in Figure 41-2):

Reconstruct first volume data slice, i = 1.
For each slice, i = 1 to number of data slices - 1:
1. Reconstruct slice i + 1.
2. For each sample slice between data slices i and i + 1:
  1. Read reconstructed values from slice i and i + 1.
  2. Perform the final LERP (for trilinear filtering).
  3. Shade and light the fragment.

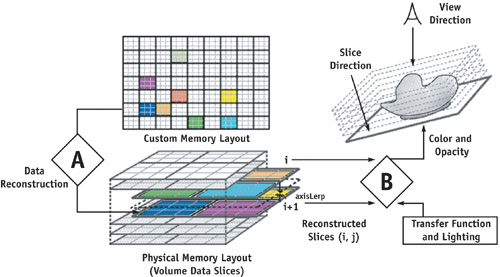
Figure 41-2 Rendering from a Custom Memory Format Using Deferred Filtering

Now, instead of reconstructing and filtering the data for each fragment rendered, we reconstruct the data at its native resolution and let the GPU's texture engine do the bulk of the filtering. The savings are dramatic: 3 fragment instructions (2 texture reads and 1 LERP) compared to 54 fragment instructions for single-pass reconstruction and rendering. Naturally, there is some overhead for the additional pass, which must include the reconstruction cost (but only once per texel). Be sure to avoid unnecessary texture copies by using render-to-texture (such as pbuffers) for slice textures i and i + 1.

The function in Listing 41-1 shows the three instructions needed to read a trilinearly filtered 3D texture by using deferred filtering. Notice that the axisLerp variable is a constant. Because we are using axis-aligned slicing, we know that every fragment rendered for the current slice will have the exact same texture coordinate along the slice axis; that is, the axisLerp represents the slice's position within the current voxel and is constant across the entire slice (see Figure 41-2).

Example 41-1. A Cg Function for a Trilinearly Filtered 3D Texture Read Using Deferred Filtering

This code would be used in step B of Figure 41-2.

 float4 deferredTex3D(float2 texCoord2D, // slice texcoord    const uniform float axisLerp,        // major axis pos    uniform sampler2D textureI,           // tex slice "i"      uniform sampler2D textureJ)           // tex slice "j"  {    float4 texValI = tex2D(textureI, texCoord);    float4 texValJ = tex2D(textureJ, texCoord);    return lerp(texValI, texValJ, axisLerp);  }

When the data set is stored as 2D slices of a 3D domain, we can easily volume-render it if the preferred slice axis corresponds to the axis along which the data was sliced for storage, as shown in part A of Figure 41-3. When the slice axis is perpendicular to the storage slice axis, the data are reconstructed from lines of the 2D storage layout, as shown in part B of Figure 41-3.

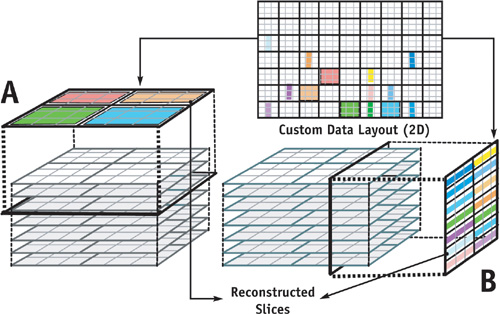
Figure 41-3 Reconstructing 3D Data from a Custom 2D Memory Layout

Although there is some overhead for the separate reconstruction and filtering passes, in general we observed speedups from 2x to 10x in practice. In Figure 41-4, we show the timings for an implementation using deferred filtering to render from a compressed volume format. We can see that in some cases, deferred filtering is even faster than nearest-neighbor filtering. This is because when sampling more than once per voxel, nearest-neighbor filtering will perform redundant reconstruction.

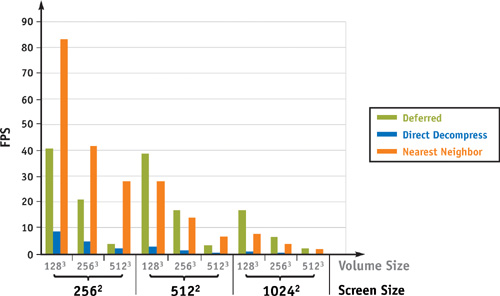
Figure 41-4 A Comparison of Various Filtering Methods

41.4 Why It Works

The major problem with reconstructing and filtering custom data formats without deferred filtering is that, for a given rendered fragment, there are often many neighboring fragments that reconstruct identical values. The burden of this obvious inefficiency increases greatly as the cost of reconstruction goes up.

For the foreseeable future, the hard-wired efficiency of the GPU texturing and filtering engine will greatly exceed that of "hand-coded" fragment program trilinear filtering. Lifting computation from the fragment program to the appropriate built-in functional units will nearly always be a performance win. In the examples and algorithm, we assume the use of trilinear interpolation. However, even when we implement a higher-order filtering scheme, deferred filtering is still a big win (see Hadwiger et al. 2001). As the filter support grows (that is, as the number of data samples required for filtering increases), so does the redundancy (and therefore cost) of reconstruction. Deferred filtering guarantees that the cost of reconstruction is incurred only once per texel.

Depending on your memory layout, other, more subtle issues come into play. Multidimensional cache coherence is an important mechanism that GPUs utilize to achieve their stellar performance. Reading multiple texels from disparate memory locations can cause significant cache-miss latency, thus increasing render times. Deferred filtering may not be able to entirely prevent this effect, but it ensures that such problems happen only once per texel rather than eight times per fragment.

41.5 Conclusions: When to Defer

The need to represent volume data in difficult formats arises in two scenarios. The first case is when the data are stored on the GPU in a compressed format, as in our example earlier. The second case arises when the 3D data are generated by the GPU (that is, dynamic volumes). Dynamic volumes arise when performing GPGPU techniques for simulation, image processing, or segmentation/morphing. Current GPU memory models require us to store dynamic volume data either in a collection of 2D textures or as a "flat 3D texture" (see Chapter 33 of this book, "Implementing Efficient Parallel Data Structures on GPUs," for more details). Rendering the collection of 2D textures requires a new variant of 2D-texture-based volume rendering that uses only a single set of 2D slices described earlier. Deferred filtering frees you from worrying about whether or not your GPGPU computational data structure is suitable for interactive rendering. Deferred filtering makes it possible to interactively render images from any of these data formats.

Deferred filtering is efficient in both time and space because it nearly eliminates reconstruction costs (because they are incurred only once per texel) and is incremental (requiring only two slices at a time). Even if the reconstruction cost is negligible, it is still more efficient to add the deferred reconstruction pass than to filter the data in a fragment program for each fragment.

One disadvantage of deferred filtering is the fact that it requires us to "split" our fragment programs. In general, this isn't a problem, because texture reads often occur up front before other computation. When the texture read is dependent on other computation, however, using deferred filtering may require sophisticated multipass partitioning schemes (Chan et al. 2002, Foley et al. 2004, Riffel et al. 2004).

41.6 References

Chan, Eric, Ren Ng, Pradeep Sen, Kekoa Proudfoot, and Pat Hanrahan. 2002. "Efficient Partitioning of Fragment Shaders for Multipass Rendering on Programmable Graphics Hardware." In Proceedings of Graphics Hardware 2002, pp. 69–78. This paper, along with Foley et al. 2004 and Riffel et al. 2004, demonstrates automatic methods for multipass partitioning of fragment programs.

Foley, Tim, Mike Houston, and Pat Hanrahan. 2004. "Efficient Partitioning of Fragment Shaders for Multiple-Output Hardware." In Proceedings of Graphics Hardware 2004.

Hadwiger, Markus, Thomas Theußl, Helwig Hauser, and Eduard Gröller. 2001. "Hardware-Accelerated High-Quality Filtering on PC Hardware." In Proceedings of Vision, Modeling, and Visualization 2001, pp. 105–112.

Harris, Mark J. 2004. "Fast Fluid Dynamics Simulation on the GPU." In GPU Gems, edited by Randima Fernando, pp. 637–665. Addison-Wesley.

Ikits, Milan, Joe Kniss, Aaron Lefohn, and Charles Hansen. 2004. "Volume Rendering Techniques." In GPU Gems, edited by Randima Fernando, pp. 667–692. Addison-Wesley.

Lefohn, A. E., J. M. Kniss, C. D. Hansen, and R. T. Whitaker. 2004. "A Streaming Narrow-Band Algorithm: Interactive Deformation and Visualization of Level Sets." IEEE Transactions on Visualization and Computer Graphics 10(2). Available online at http://graphics.idav.ucdavis.edu/~lefohn/work/pubs/ This paper describes an efficient GPGPU algorithm for sparse, nonlinear partial differential equations that permit real-time morphing and animation. This algorithm dynamically remaps data blocks to ensure that only the necessary, active data blocks receive computation. The authors describe how deferred filtering works in their rendering pipeline.

Rezk-Salama, C., K. Engel, M. Bauer, G. Greiner, and T. Ertl. 2000. "Interactive Volume Rendering on Standard PC Graphics Hardware Using Multi-Textures and Multi-Stage Rasterization." In Proceedings of the SIGGRAPH/Eurographics Workshop on Graphics Hardware 2000, pp. 109–118. These authors were among the first to leverage the capabilities of programmable graphics hardware for volume rendering. They were also the first to demonstrate trilinear interpolation of 3D textures stored as 2D slices.

Riffel, Andrew T., Aaron E. Lefohn, Kiril Vidimce, Mark Leone, and John D. Owens. 2004. "Mio: Fast Multipass Partitioning via Priority-Based Instruction Scheduling." In Proceedings of Graphics Hardware 2004.

Schneider, J., and R. Westermann. 2003. "Compression Domain Volume Rendering." In Proceedings of IEEE Visualization 2003, pp. 293–300. This article presents an approach for volume data (3D) compression using vector quantization that allows decompression during rendering using programmable graphics hardware.

Copyright

Many of the designations used by manufacturers and sellers to distinguish their products are claimed as trademarks. Where those designations appear in this book, and Addison-Wesley was aware of a trademark claim, the designations have been printed with initial capital letters or in all capitals.

The authors and publisher have taken care in the preparation of this book, but make no expressed or implied warranty of any kind and assume no responsibility for errors or omissions. No liability is assumed for incidental or consequential damages in connection with or arising out of the use of the information or programs contained herein.

NVIDIA makes no warranty or representation that the techniques described herein are free from any Intellectual Property claims. The reader assumes all risk of any such claims based on his or her use of these techniques.

The publisher offers excellent discounts on this book when ordered in quantity for bulk purchases or special sales, which may include electronic versions and/or custom covers and content particular to your business, training goals, marketing focus, and branding interests. For more information, please contact:

U.S. Corporate and Government Sales
(800) 382-3419
corpsales@pearsontechgroup.com

For sales outside of the U.S., please contact:

International Sales
international@pearsoned.com

Visit Addison-Wesley on the Web: www.awprofessional.com

Library of Congress Cataloging-in-Publication Data

GPU gems 2 : programming techniques for high-performance graphics and general-purpose
computation / edited by Matt Pharr ; Randima Fernando, series editor.
p. cm.
Includes bibliographical references and index.
ISBN 0-321-33559-7 (hardcover : alk. paper)
1. Computer graphics. 2. Real-time programming. I. Pharr, Matt. II. Fernando, Randima.

T385.G688 2005
006.66—dc22
2004030181

GeForce™ and NVIDIA Quadro® are trademarks or registered trademarks of NVIDIA Corporation.

mental images and mental ray are trademarks or registered trademarks of mental images, GmbH.

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form, or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior consent of the publisher. Printed in the United States of America. Published simultaneously in Canada.

For information on obtaining permission for use of material from this work, please submit a written request to:

Pearson Education, Inc.
Rights and Contracts Department
One Lake Street
Upper Saddle River, NJ 07458

Text printed in the United States on recycled paper at Quebecor World Taunton in Taunton, Massachusetts.

Second printing, April 2005

Dedication

To everyone striving to make today's best computer graphics look primitive tomorrow

Part II: Shading, Lighting, and Shadows

Part III: High-Quality Rendering

Part IV: General-Purpose Computation on GPUS: A Primer

Part V: Image-Oriented Computing

Part VI: Simulation and Numerical Algorithms