GPU Gems 2

GPU Gems 2

GPU Gems 2 is now available, right here, online. You can purchase a beautifully printed version of this book, and others in the series, at a 30% discount courtesy of InformIT and Addison-Wesley.

The CD content, including demos and content, is available on the web and for download.

Chapter 26. Implementing Improved Perlin Noise

Simon Green
NVIDIA Corporation

This chapter follows up on Ken Perlin's chapter in GPU Gems, "Implementing Improved Perlin Noise" (Perlin 2004). Whereas Ken's chapter discussed how to implement fast approximations to procedural noise using 3D textures, here we describe a working GPU implementation of the improved noise algorithm in both Microsoft Direct 3D Effects (FX) and CgFX syntax that exactly matches the reference CPU implementation.

26.1 Random but Smooth

Noise is an important building block for adding natural-looking variety to procedural textures. In the real world, nothing is perfectly uniform, and noise provides a controlled way of adding this randomness to your shaders.

The noise function has several important characteristics:

  • It produces a repeatable pseudorandom value for each input position.
  • It has a known range (usually [-1, 1]).
  • It has band-limited spatial frequency (that is, it is smooth).
  • It doesn't show obvious repeating patterns.
  • Its spatial frequency is invariant under translation.

Perlin's improved noise algorithm meets all these requirements (Perlin 2002). We now go on to explain how it can be implemented on the GPU.

26.2 Storage vs. Computation

Procedural noise is typically implemented in today's shaders using precomputed 3D textures. Implementing noise directly in the pixel shader has several advantages over this approach:

  • It requires less texture memory.
  • The period is large (that is, the pattern doesn't repeat as often).
  • The results match existing CPU implementations exactly.
  • It allows four-dimensional noise, which is useful for 3D effects with animation. (Current hardware doesn't support 4D textures.)
  • The interpolation used is higher quality than what is available with hardware texture filtering, which results in smoother-looking noise.

Figure 26-1a shows the result of using a 3D texture to render an object with noise. Note the artifacts due to linear interpolation being used for texture map filtering. In contrast, the image in Figure 26-1b, which shows the result of using the procedural approach described in this chapter, is substantially better.

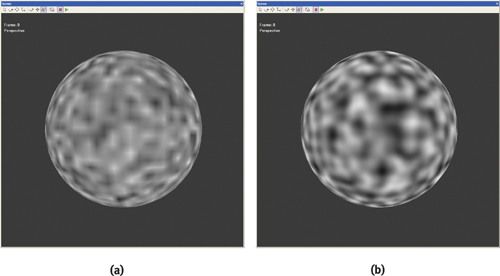
26_noise_01a.jpg

Figure 26-1 3D Noise

The obvious disadvantage of this approach is that it is more computationally expensive. This is largely because we have to perform the interpolation in the shader, and are not taking advantage of the texture-filtering hardware present in the GPU. The optimized implementation of 3D noise compiles to around 50 Pixel Shader 2.0 instructions using the latest compilers; fortunately, this doesn't pose a challenge for current high-end GPUs.

26.3 Implementation Details

Perlin's noise algorithm consists of two main stages.

The first stage generates a repeatable pseudorandom value for every integer (x, y, z) position in 3D space. This can be achieved in several ways, but Perlin's algorithm uses a hash function. The hash function is based on a permutation table that contains the integers from 0 to 255 in random order. (This table can be standardized between implementations so that they produce the same results.) First the table is indexed based on the x coordinate of the position. Then the y coordinate is added to the value at this position in the table, and the result is used to look up in the table again. After this process is repeated for the z coordinate, the result is a pseudorandom integer for every possible (x, y, z) position.

In the second stage of the algorithm, this pseudorandom integer is used to index into a table of 3D gradient vectors. In the "improved" algorithm, only eight different gradients are used. A scalar value is calculated by taking the dot product between the gradient and the fractional position within the noise space. The final value is obtained by interpolating between the noise values for each of the neighboring eight points in space.

The CPU implementation of Perlin's improved noise algorithm stores the permutation and gradient tables in arrays. Pixel shaders do not currently support indexing into constant memory, so instead we store these tables in textures and use texture lookups to access them. The texture addressing is set to wrap (or repeat) mode, so we don't have to worry about extending the tables to avoid indexing past the end of the array, as is done in the CPU implementation. Listing 26-1 shows how these textures can be initialized in an FX file.

One of the most useful features of the Microsoft Direct 3D Effects and CgFX runtimes is a virtual machine that can be used to procedurally generate textures from functions. We use this feature to build the permutation and gradient textures from the same data given in the reference implementation. If you are using another shading language, such as the OpenGL Shading Language, it should be trivial to include this code in your application instead.

Example 26-1. Source Code for Initializing the Permutation Texture for Noise

 // permutation table  static int permutation[] = {    151, /* 254 values elided . . . */, 180  };    // Generate permutation and gradient textures using CPU runtime  texture permTexture  <    string texturetype = "2D";    string format = "l8";    string function = "GeneratePermTexture";    int width = 256, height = 1;    >;    float4 GeneratePermTexture(float p : POSITION) : COLOR  {    return permutation[p * 256] / 255.0;  }    sampler permSampler = sampler_state  {    texture = <permTexture>;    AddressU  = Wrap;    AddressV  = Clamp;    MAGFILTER = POINT;    MINFILTER = POINT;    MIPFILTER = NONE;  };

The reference implementation uses bit-manipulation code to generate the gradient vectors directly from the hash values. Because current pixel shader hardware does not include integer operations, this method is not feasible, so instead we precalculate a small 1D texture containing the 16 gradient vectors. The code to generate this texture is shown in Listing 26-2.

The final code that uses these two textures to compute noise values is given in Listing 26-3. It includes Perlin's new interpolation function, which is a Hermite polynomial of degree five and results in a C2 continuous noise function. Alternatively, you can also use the original interpolation function, which is less expensive to evaluate but results in discontinuous second derivatives.

Example 26-2. Source Code to Compute Gradient Texture for Noise

 // gradients for 3D noise  static float3 g[] = {    1,1,0,    -1,1,0,    1,-1,0,    -1,-1,0,    1,0,1,    -1,0,1,    1,0,-1,    -1,0,-1,    0,1,1,    0,-1,1,    0,1,-1,    0,-1,-1,    1,1,0,    0,-1,1,    -1,1,0,    0,-1,-1,  };    texture gradTexture  <    string texturetype = "2D";    string format = "q8w8v8u8";    string function = "GenerateGradTexture";    int width = 16, height = 1;    >;    float3 GenerateGradTexture(float p : POSITION) : COLOR  {    return g[p * 16];  }    sampler gradSampler = sampler_state  {    texture = <gradTexture>;    AddressU  = Wrap;    AddressV  = Clamp;    MAGFILTER = POINT;    MINFILTER = POINT;    MIPFILTER = NONE;  };

Example 26-3. Source Code for Computing 3D Perlin Noise Function

 float3 fade(float3 t)  {    return t * t * t * (t * (t * 6 - 15) + 10); // new curve  //  return t * t * (3 - 2 * t); // old curve  }    float perm(float x)  {    return tex1D(permSampler, x / 256.0) * 256;  }    float grad(float x, float3 p)  {    return dot(tex1D(gradSampler, x), p);  }    // 3D version  float inoise(float3 p)  {    float3 P = fmod(floor(p), 256.0);    p -= floor(p);    float3 f = fade(p);      // HASH COORDINATES FOR 6 OF THE 8 CUBE CORNERS      float A = perm(P.x) + P.y;    float AA = perm(A) + P.z;    float AB = perm(A + 1) + P.z;    float B =  perm(P.x + 1) + P.y;    float BA = perm(B) + P.z;    float BB = perm(B + 1) + P.z;      // AND ADD BLENDED RESULTS FROM 8 CORNERS OF CUBE      return lerp(      lerp(lerp(grad(perm(AA), p),                grad(perm(BA), p + float3(-1, 0, 0)), f.x),           lerp(grad(perm(AB), p + float3(0, -1, 0)),                grad(perm(BB), p + float3(-1, -1, 0)), f.x), f.y),      lerp(lerp(grad(perm(AA + 1), p + float3(0, 0, -1)),                grad(perm(BA + 1), p + float3(-1, 0, -1)), f.x),           lerp(grad(perm(AB + 1), p + float3(0, -1, -1)),                grad(perm(BB + 1), p + float3(-1, -1, -1)), f.x), f.y),      f.z);  }

This same code could be also be compiled for the vertex shader with some modifications. Vertex shaders support variable indexing into constant memory, so it is not necessary to use texture lookups.

For brevity, the code in Listing 26-3 provides the implementation for only 3D noise. The version of the code on this book's CD includes the 4D version.

26.3.1 Optimization

The code in Listing 26-3 is a straightforward port of the reference CPU implementation. There are several ways this code can be optimized to take better advantage of the graphics hardware. (The optimized code is included on the accompanying CD, along with the implementation for 4D noise.)

The reference implementation uses six recursive lookups into the permutation table to generate the initial four hash values. The obvious way to implement this on the GPU is as six texture lookups into a 1D texture, but instead we can precalculate a 256x256-pixel RGBA 2D texture that contains four values in each texel, and use a single 2D lookup.

We can also remove the final lookup into the permutation table by expanding the gradient table and permuting the gradients. So instead of using a 16-pixel gradient texture, we create a 256-pixel texture with the gradients rearranged based on the permutation table. This eliminates eight 1D texture lookups.

The unoptimized implementation compiles to 81 Pixel Shader 2.0 instructions, including 22 texture lookups. After optimization, it is 53 instructions, only nine of which are texture lookups.

Because much of the code is scalar, there may also be potential for taking more advantage of vector operations.

26.4 Conclusion

We have described an implementation of procedural noise for pixel shaders. Procedural noise is an important building block for visually rich rendering, and it can be used for bump mapping and other effects, as shown in Figure 26-2. Although developers of most real-time applications running on today's GPUs will not want to dedicate 50 pixel shader instructions to a single noise lookup, this technique is useful for high-quality, offline-rendering applications, where matching existing CPU noise implementations is important. As the computational capabilities of GPUs increase and memory access becomes relatively more expensive due to continued hardware trends, procedural techniques such as this will become increasingly attractive.

26_noise_2.jpg

Figure 26-2 Pixel Shader Noise Used for Procedural Bump Mapping

26.5 References

Ebert, David S., F. Kenton Musgrave, Darwyn Peachey, Ken Perlin, and Steven Worley. 2003. Texturing and Modeling: A Procedural Approach, 3rd ed. Morgan Kaufmann.

Perlin, Ken. 2004. "Implementing Improved Perlin Noise." In GPU Gems, edited by Randima Fernando, pp. 73–85. Addison-Wesley.

Perlin, Ken. 2002. "Improving Noise." ACM Transactions on Graphics (Proceedings of SIGGRAPH 2002) 21(3), pp. 681–682. Updated version available online at http://mrl.nyu.edu/~perlin/noise/

Perlin, Ken. 1985. "An Image Synthesizer." In Computer Graphics (Proceedings of ACM SIGGRAPH 85) 19(3), pp. 287–296.

Copyright

Many of the designations used by manufacturers and sellers to distinguish their products are claimed as trademarks. Where those designations appear in this book, and Addison-Wesley was aware of a trademark claim, the designations have been printed with initial capital letters or in all capitals.

The authors and publisher have taken care in the preparation of this book, but make no expressed or implied warranty of any kind and assume no responsibility for errors or omissions. No liability is assumed for incidental or consequential damages in connection with or arising out of the use of the information or programs contained herein.

NVIDIA makes no warranty or representation that the techniques described herein are free from any Intellectual Property claims. The reader assumes all risk of any such claims based on his or her use of these techniques.

The publisher offers excellent discounts on this book when ordered in quantity for bulk purchases or special sales, which may include electronic versions and/or custom covers and content particular to your business, training goals, marketing focus, and branding interests. For more information, please contact:

U.S. Corporate and Government Sales
(800) 382-3419
corpsales@pearsontechgroup.com

For sales outside of the U.S., please contact:

International Sales
international@pearsoned.com

Visit Addison-Wesley on the Web: www.awprofessional.com

Library of Congress Cataloging-in-Publication Data

GPU gems 2 : programming techniques for high-performance graphics and general-purpose
computation / edited by Matt Pharr ; Randima Fernando, series editor.
p. cm.
Includes bibliographical references and index.
ISBN 0-321-33559-7 (hardcover : alk. paper)
1. Computer graphics. 2. Real-time programming. I. Pharr, Matt. II. Fernando, Randima.

T385.G688 2005
006.66—dc22
2004030181

GeForce™ and NVIDIA Quadro® are trademarks or registered trademarks of NVIDIA Corporation.

Nalu, Timbury, and Clear Sailing images © 2004 NVIDIA Corporation.

mental images and mental ray are trademarks or registered trademarks of mental images, GmbH.

Copyright © 2005 by NVIDIA Corporation.

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form, or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior consent of the publisher. Printed in the United States of America. Published simultaneously in Canada.

For information on obtaining permission for use of material from this work, please submit a written request to:

Pearson Education, Inc.
Rights and Contracts Department
One Lake Street
Upper Saddle River, NJ 07458

Text printed in the United States on recycled paper at Quebecor World Taunton in Taunton, Massachusetts.

Second printing, April 2005

Dedication

To everyone striving to make today's best computer graphics look primitive tomorrow