
GPU Gems 2
GPU Gems 2 is now available, right here, online. You can purchase a beautifully printed version of this book, and others in the series, at a 30% discount courtesy of InformIT and Addison-Wesley.
The CD content, including demos and content, is available on the web and for download.
Chapter 34. GPU Flow-Control Idioms
Mark Harris
NVIDIA Corporation
Ian Buck
Stanford University
Flow control is one of the most fundamental concepts taught to beginning programmers. Branching and looping are such basic concepts that it can be daunting to write software for a platform that supports them in a limited manner. The latest GPUs support vertex and fragment program branching in multiple forms, but their highly parallel nature requires care in how they are used. This chapter surveys some of the limitations of branching on current GPUs and describes a variety of techniques for iteration and decision making in GPGPU programs.
34.1 Flow-Control Challenges
Let's start by discussing the most obvious form of flow control on GPUs. All current high-level shading languages for GPUs support traditional C-style explicit flow-control constructs, such as if-then-else, for, and while. The underlying implementations of these, however, are much different from their implementations on CPUs.
For example, consider the following code:
if (a)
b = f();
else
b = g();CPUs can easily branch based on the Boolean a and evaluate either the f() or g() functions. The performance characteristics of this branch are relatively easily understood: CPUs generally have long instruction pipelines, so it is important that the CPU be able to accurately predict whether a particular branch will be taken. If this prediction is done successfully, branching generally incurs a small penalty. If the branch is not correctly predicted, the CPU may stall for a number of cycles as the pipeline is flushed and must be refilled from the correct target address. As long as the functions f() and g() have a reasonable number of instructions, these costs aren't too high.
The latest GPUs, such as the NVIDIA GeForce 6 Series, have similar branch instructions, though their performance characteristics are slightly different. Older GPUs do not have native branching of this form, so other strategies are necessary to emulate these operations.
The two most common control mechanisms in parallel architectures are single instruction, multiple data (SIMD) and multiple instruction, multiple data (MIMD). All processors in a SIMD-parallel architecture execute the same instruction at the same time; in a MIMD-parallel architecture, different processors may simultaneously execute different instructions. There are three current methods used by GPUs to implement branching: MIMD branching, SIMD branching, and condition codes.
MIMD branching is the ideal case, in which different processors can take different data-dependent branches without penalty, much like a CPU. The NVIDIA GeForce 6 Series supports MIMD branching in its vertex processors.
SIMD branching allows branching and looping inside a program, but because all processors must execute identical instructions, divergent branching can result in reduced performance. For example, imagine a fragment program that decides the output value of each fragment by branching using conditions based on random input numbers. The fragments will randomly take different branches, which can cause processors that are running threads for fragments that do not take the branch to stall until other processors are finished running threads for fragments that do take the branch. The end result is that many fragments will take as long as both branches together, plus the overhead of the branch instruction. SIMD branching is very useful in cases where the branch conditions are fairly "spatially" coherent, but lots of incoherent branching can be expensive. NVIDIA GeForce FX GPUs support SIMD branching in their vertex processors, and NVIDIA GeForce 6 Series GPUs support it in their fragment processors.
Condition codes (predication) are used in older architectures to emulate true branching. If-then statements compiled to these architectures must evaluate both taken and not taken branch instructions on all fragments. The branch condition is evaluated and a condition code is set. The instructions in each part of the branch must check the value of the condition code before writing their results to registers. As a result, only instructions in taken branches write their output. Thus, in these architectures all branches cost as much as both parts of the branch, plus the cost of evaluating the branch condition. Branching should be used sparingly on such architectures. NVIDIA GeForce FX Series GPUs use condition-code branch emulation in their fragment processors.
34.2 Basic Flow-Control Strategies
34.2.1 Predication
The simplest approach to implementing branching on the GPU is predication, as discussed earlier. With predication, the GPU effectively evaluates both sides of the branch and then discards one of the results, based on the value of the Boolean branch condition. The disadvantage of this approach is that evaluating both sides of the branch can be costly if f() and g() are large functions. While predication may be effective for small branches, alternative strategies are necessary for more complex branching.
34.2.2 Moving Branching up the Pipeline
Because explicit branching can be tricky on GPUs, it's handy to have a number of techniques in your repertoire. A useful strategy is to move flow-control decisions up the pipeline to an earlier stage, where they can be more efficiently evaluated.
Static Branch Resolution
When performing computations on streams or arrays of data on the CPU, most programmers know that they should strive to avoid branching inside the inner loops of the computation. Doing so can cause the pipeline to stall due to incorrect branch prediction. For example, consider evaluating a partial differential equation (PDE) on a discrete spatial grid. Correct evaluation of the PDE on a finite domain requires boundary conditions. A naive CPU implementation might iterate over the entire grid, deciding at each cell if it is a boundary cell and applying the appropriate computation based on the result of the decision. A better implementation divides the processing into multiple loops: one over the interior of the grid, excluding boundary cells, and one or more over the boundary edges. This static branch resolution results in loops that contain efficient code without branches.
The same optimization is even more important on most GPUs. In this case, the computation is divided into two fragment programs: one for interior cells and one for boundary cells. The interior program is applied to the fragments of a quad drawn over all but the outer single-cell-wide edge of the output buffer. The boundary program is applied to fragments of lines drawn over the edge pixels.
Precomputation
In the preceding example, the result of a branch was constant over a large domain of input (or range of output) values. Similarly, sometimes the result of a branch is constant for a period of time or a number of iterations of a computation. In this case, we can evaluate the branches only when the results change, and store the results for use over many subsequent iterations. This can result in a large performance boost.
The "gpgpu_fluid" example in the NVIDIA SDK uses this technique to avoid branching when computing boundary conditions at the edges of arbitrary obstacles in the flow field. In this case, fluid cells with no neighboring obstacles can be processed normally, but cells with neighboring obstacles require more work. These cells must check their neighbors to figure out in which direction the obstacle lies, and they use this direction to look up more data to be used in the computation. In the example, the obstacles change only when the user "paints" them. Therefore, we can precompute the offset direction and store it in an offset texture to be reused until the user changes the obstacles again.
34.2.3 Z-Cull
We can take precomputed branch results a step further and use another GPU feature to entirely skip unnecessary work. Modern GPUs have a number of features designed to avoid shading pixels that will not be seen. One of these is z-cull. Z-cull is a technique for comparing the depth (z) of incoming fragments with the depth of the corresponding fragments in the z-buffer such that if the incoming fragments fail the depth test, they are discarded before their pixel colors are calculated in the fragment processor. Thus, only fragments that pass the depth test are processed, work is saved, and the application runs faster.
We can use this technique for general-purpose computation, too. In the example of obstacles in fluid flow given earlier, there are some cells that are completely "landlocked": all of their neighbors are obstacle cells. We don't need to do any computation on these cells. To skip these cells, we do a bit of setup work whenever the user paints new obstacles. We run a fragment program that examines the neighbors of each fragment. The program draws only fragments that are landlocked and discards all others using the discard keyword. (The discard keyword is available in Cg and GLSL. The HLSL equivalent is clip()). The Cg code for this program is shown in Listing 34-1. The pseudocode that follows in Listing 34-2 demonstrates how z-cull is set up and then used to skip processing of landlocked cells.
What happens in the code in these two listings is that the preprocessing pass sets up a "mask" in the z-buffer where landlocked cells have a depth of 0.0 and all other cells have a depth of 1.0. Therefore, when we draw a quad at z = 0.5, the landlocked cells will be "blocked" by the values of 0.0 in the z-buffer and will be automatically culled by the GPU. If the obstacles are fairly large, then we will save a lot of work by not processing these cells.
Example 34-1. Cg Code to Set Z-Depth Values for Z-Culling in Subsequent Passes
half obstacles(half2 coords : WPOS, uniform samplerRECT obstacleGrid) : COLOR
{
// get neighboring boundary values (on or off)
half4 bounds;
bounds.x = texRECT(obstacleGrid, coords - half2(1, 0)).x;
bounds.y = texRECT(obstacleGrid, coords + half2(1, 0)).x;
bounds.z = texRECT(obstacleGrid, coords - half2(0, 1)).x;
bounds.w = texRECT(obstacleGrid, coords + half2(0, 1)).x;
bounds.x = dot(bounds, (1).xxxx); // add them up
// discard cells that are not landlocked
if (bounds.x < 4)
discard;
return 0;
}Example 34-2. Application Pseudocode
We set z values in the first pass. In the second pass, we execute a fragment program at pixels where the z test passes.
// Application Code--Preprocess pass
ClearZBuffer(1.0);
Enable(DEPTH_TEST);
DepthFunc(LESS);
BindFragmentProgram("obstacles");
DrawQuad(Z = 0.0);
// Application code--Passes in which landlocked cells are to be skipped
Enable(DEPTH_TEST);
Disable(DEPTH_WRITE); // want to read depth, but not modify it
DepthFunc(LESS);
// bind normal fragment program for each pass
DrawQuad(Z = 0.5);One caveat with this technique is that z-culling is often performed by the GPU at a coarser resolution than a per-fragment basis. The GPU will skip shading operations only if all the fragments in a small contiguous region of the frame buffer fail the depth test. The exact size of this region varies from GPU to GPU, but in general, z-cull will provide a performance improvement only if your branches have some locality.
To illustrate this, we can compare the performance of z-cull with a random Boolean condition versus a Boolean condition with high spatial locality. For the random Boolean case, we fill a texture with random values. For the Boolean with high spatial locality, we simply set a rectangular region to a constant Boolean value.
As you can see from Figure 34-1, z-cull is most effective if there is plenty of locality in the branch. The good news is that this locality is naturally present if the probability of taking the branch is either very low (that is, if very few fragments pass the depth test) or very high. If locality is not present, z-cull is not much better than predication.
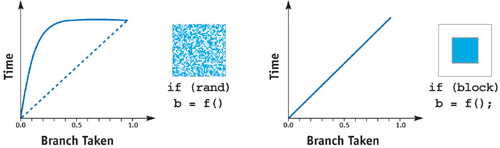
Figure 34-1 The Costs of Different Types of Branches When Using Z-Cull
Note, however, that z-cull is very different from branching inside a fragment program. Z-cull prevents the fragment program from ever executing. Therefore, z-cull is a powerful method for skipping lots of unnecessary work based on a static, preevaluated condition. To do the same with fragment program branching would require the program to be executed, the condition to be evaluated, and the program to exit early. All of this requires more processor cycles than skipping the fragment program altogether.
34.2.4 Branching Instructions
The first GPUs to support fragment branching instructions are the NVIDIA GeForce 6 Series. These instructions are available with both the Microsoft DirectX Pixel Shader 3.0 instruction set and the OpenGL NV_fragment_program2 extension. As more GPUs support branch instructions, using predication for branching should no longer be necessary. Note, however, that the locality issues that affect early z-cull also apply to these branch instructions. GPUs execute fragment programs on groups of fragments in parallel, where each group can execute only one branch. Where this is not possible, the GPU will effectively fall back to predication. Figure 34-2 shows the time versus probability test implemented using branch instructions.
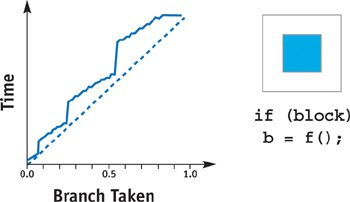
Figure 34-2 The Costs of Different Types of Branches with Pixel Shader 3.0
As you can see, the same spatial locality caveat applies to branching efficiency. However, as with z-cull, if the branch has either a very low or a very high probability, branching instructions are quite effective.
34.2.5 Choosing a Branching Mechanism
Choosing an effective branching mechanism for your program depends primarily on the amount of code inside a branch and the amount of state present. For short branches—two to four operations—predication is preferred, because the overhead for either z-cull or the branching instructions can negate any benefits. For branches that are embedded in larger programs, consider using the branching instructions rather than z-cull. Even though the branching instructions are more sensitive to locality issues, using z-cull requires you to save all program state, execute the branch in a separate pass, and restore the state of the program to continue. For large programs, these saves and restores can make z-culling inefficient. However, if we can effectively isolate the branch component of our program, z-cull can provide the best performance.
34.3 Data-Dependent Looping with Occlusion Queries
Another GPU feature designed to avoid drawing what is not visible is the hardware occlusion query. This feature enables you to query the number of pixels updated by a rendering call. Such queries are pipelined, which means that they provide a way to get a limited amount of data (an integer count) back from the GPU without stalling the pipeline, as occurs when we read back actual pixels. Because in GPGPU we are almost always drawing quads with known pixel coverage, we can use occlusion query with the discard keyword discussed in Section 34.2.3 to get a count of fragments updated and discarded. This allows us to implement global decisions controlled by the CPU based on GPU processing.
Suppose we have a computation that needs to proceed iteratively on elements of a stream until all elements satisfy a termination criterion. To implement this on the GPU, we write a fragment program that implements the computation and one that tests the termination criterion. The latter program discards fragments that satisfy the termination criterion. We then write a loop on the CPU like the following pseudocode, which will execute until all stream elements satisfy the termination criteria.
int numberNotTerminated = streamSize;
while (numberNotTerminated > 0)
{
gpuRunProgram(computationProgram);
gpuBeginQuery(myQuery);
gpuRunProgram(terminationProgram);
gpuEndQuery(myQuery);
numberNotTerminated = gpuGetQueryResults(myQuery);
}This technique can also be used for subdivision algorithms, such as the adaptive radiosity solution in Chapter 39 of this book, "Global Illumination Using Progressive Refinement Radiosity."
34.4 Conclusion
With their support for branching at the fragment processor level, the latest generation of GPUs makes branching much easier to use in GPGPU programs. Higher-level language constructs such as if, for, and while compile directly to GPU assembly instructions, freeing the developer from having to use more complex strategies such as z-cull and occlusion queries, as is necessary on earlier GPUs.
Nevertheless, there is still a penalty for incoherent branching on GPUs. Employing techniques based on precomputation and moving computation higher up the pipeline—either to the vertex processing unit or to the CPU, as described in Section 34.2.2—will continue to be a useful GPGPU strategy.
Copyright
Many of the designations used by manufacturers and sellers to distinguish their products are claimed as trademarks. Where those designations appear in this book, and Addison-Wesley was aware of a trademark claim, the designations have been printed with initial capital letters or in all capitals.
The authors and publisher have taken care in the preparation of this book, but make no expressed or implied warranty of any kind and assume no responsibility for errors or omissions. No liability is assumed for incidental or consequential damages in connection with or arising out of the use of the information or programs contained herein.
NVIDIA makes no warranty or representation that the techniques described herein are free from any Intellectual Property claims. The reader assumes all risk of any such claims based on his or her use of these techniques.
The publisher offers excellent discounts on this book when ordered in quantity for bulk purchases or special sales, which may include electronic versions and/or custom covers and content particular to your business, training goals, marketing focus, and branding interests. For more information, please contact:
U.S. Corporate and Government Sales
(800) 382-3419
corpsales@pearsontechgroup.com
For sales outside of the U.S., please contact:
International Sales
international@pearsoned.com
Visit Addison-Wesley on the Web: www.awprofessional.com
Library of Congress Cataloging-in-Publication Data
GPU gems 2 : programming techniques for high-performance graphics and general-purpose
computation / edited by Matt Pharr ; Randima Fernando, series editor.
p. cm.
Includes bibliographical references and index.
ISBN 0-321-33559-7 (hardcover : alk. paper)
1. Computer graphics. 2. Real-time programming. I. Pharr, Matt. II. Fernando, Randima.
T385.G688 2005
006.66—dc22
2004030181
GeForce™ and NVIDIA Quadro® are trademarks or registered trademarks of NVIDIA Corporation.
Nalu, Timbury, and Clear Sailing images © 2004 NVIDIA Corporation.
mental images and mental ray are trademarks or registered trademarks of mental images, GmbH.
Copyright © 2005 by NVIDIA Corporation.
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form, or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior consent of the publisher. Printed in the United States of America. Published simultaneously in Canada.
For information on obtaining permission for use of material from this work, please submit a written request to:
Pearson Education, Inc.
Rights and Contracts Department
One Lake Street
Upper Saddle River, NJ 07458
Text printed in the United States on recycled paper at Quebecor World Taunton in Taunton, Massachusetts.
Second printing, April 2005
Dedication
To everyone striving to make today's best computer graphics look primitive tomorrow
- Copyright
- Inside Back Cover
- Inside Front Cover
- Part I: Geometric Complexity
-
- Chapter 1. Toward Photorealism in Virtual Botany
- Chapter 2. Terrain Rendering Using GPU-Based Geometry Clipmaps
- Chapter 3. Inside Geometry Instancing
- Chapter 4. Segment Buffering
- Chapter 5. Optimizing Resource Management with Multistreaming
- Chapter 6. Hardware Occlusion Queries Made Useful
- Chapter 7. Adaptive Tessellation of Subdivision Surfaces with Displacement Mapping
- Chapter 8. Per-Pixel Displacement Mapping with Distance Functions
- Part II: Shading, Lighting, and Shadows
-
- Chapter 9. Deferred Shading in S.T.A.L.K.E.R.
- Chapter 10. Real-Time Computation of Dynamic Irradiance Environment Maps
- Chapter 11. Approximate Bidirectional Texture Functions
- Chapter 12. Tile-Based Texture Mapping
- Chapter 13. Implementing the mental images Phenomena Renderer on the GPU
- Chapter 14. Dynamic Ambient Occlusion and Indirect Lighting
- Chapter 15. Blueprint Rendering and "Sketchy Drawings"
- Chapter 16. Accurate Atmospheric Scattering
- Chapter 17. Efficient Soft-Edged Shadows Using Pixel Shader Branching
- Chapter 18. Using Vertex Texture Displacement for Realistic Water Rendering
- Chapter 19. Generic Refraction Simulation
- Part III: High-Quality Rendering
-
- Chapter 20. Fast Third-Order Texture Filtering
- Chapter 21. High-Quality Antialiased Rasterization
- Chapter 22. Fast Prefiltered Lines
- Chapter 23. Hair Animation and Rendering in the Nalu Demo
- Chapter 24. Using Lookup Tables to Accelerate Color Transformations
- Chapter 25. GPU Image Processing in Apple's Motion
- Chapter 26. Implementing Improved Perlin Noise
- Chapter 27. Advanced High-Quality Filtering
- Chapter 28. Mipmap-Level Measurement
- Part IV: General-Purpose Computation on GPUS: A Primer
-
- Chapter 29. Streaming Architectures and Technology Trends
- Chapter 30. The GeForce 6 Series GPU Architecture
- Chapter 31. Mapping Computational Concepts to GPUs
- Chapter 32. Taking the Plunge into GPU Computing
- Chapter 33. Implementing Efficient Parallel Data Structures on GPUs
- Chapter 34. GPU Flow-Control Idioms
- Chapter 35. GPU Program Optimization
- Chapter 36. Stream Reduction Operations for GPGPU Applications
- Part V: Image-Oriented Computing
-
- Chapter 37. Octree Textures on the GPU
- Chapter 38. High-Quality Global Illumination Rendering Using Rasterization
- Chapter 39. Global Illumination Using Progressive Refinement Radiosity
- Chapter 40. Computer Vision on the GPU
- Chapter 41. Deferred Filtering: Rendering from Difficult Data Formats
- Chapter 42. Conservative Rasterization
- Part VI: Simulation and Numerical Algorithms
-
- Chapter 43. GPU Computing for Protein Structure Prediction
- Chapter 44. A GPU Framework for Solving Systems of Linear Equations
- Chapter 45. Options Pricing on the GPU
- Chapter 46. Improved GPU Sorting
- Chapter 47. Flow Simulation with Complex Boundaries
- Chapter 48. Medical Image Reconstruction with the FFT