As of March 21, 2023, QODA is now CUDA Quantum. For up-to-date information, see the CUDA Quantum page.
Quantum circuit simulation is the best means to design quantum-ready algorithms so you can take advantage of powerful quantum computers as soon as they are available.
NVIDIA cuQuantum is an SDK that enables you to leverage different ways to perform quantum circuit simulation. cuStateVec, a high-performance library built for state vector quantum simulators, relies on holding a quantum state vector in GPU memory. Its memory requirement scales as O(2^N), with N representing the number of qubits. This can be prohibitively expensive as you begin to scale beyond ~40 qubits.
To alleviate the exponential scaling of the memory requirement of quantum circuit simulation using the state vector method, tensor networks can be used as an alternative. You can simulate much larger quantum circuits by trading increased computation for reduced space.
cuTensorNet lets you take advantage of tensor network methods on NVIDIA GPUs, providing increased scalability and better performance when compared to other alternatives. Despite the recent progress in accelerating tensor contraction pathfinding, the cost for exact tensor network contraction can still become intractable as the circuit size increases in either depth or width.
One strategy to systematically keep the resources required for tensor network simulation tractable is to use approximation algorithms. This post details the new functionalities available in cuTensorNet v2.0.0 that support approximate tensor network simulations.
Further scale approximate tensor network simulations with cuTensorNet
Starting with v.2.0.0, the cuTensorNet library provides single GPU computational primitives to accelerate approximate tensor network simulations. As the quantum problems of interest can greatly vary in both size and complexity, researchers have developed highly customized approximate tensor network algorithms to address the gamut of possibilities.
To enable easy integration with these frameworks and libraries, cuTensorNet provides a set of APIs to cover the following common use cases:
- Tensor QR
- Tensor SVD
- Gate Split
These primitives enable you to accelerate and scale different types of quantum circuit simulators. A common approach to simulating quantum computers that takes advantage of these methods is matrix product state (MPS), also known as a tensor train.
Decomposition
QR decomposition of a matrix can be generalized to high-dimensional tensors by combining multiple dimensions of the tensor into a row dimension and the rest into a column dimension. The resulting Q and R matrices can be further unfolded into tensors, making a valid split of the input tensor into two operands.
Tensor QR
We introduce cutensornetTensorQR, an API, which is heavily used to move the orthogonality center in approximate tensor networks, including MPS, projected entangled pair states (PEPS), and more.
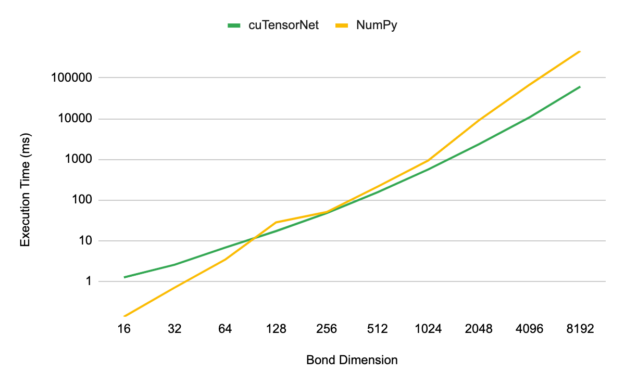
For benchmarks, we examined the performance of decomposing rank-3 MPS tensors, with shape (D, 2, D) where D denotes the bond dimension of the MPS, using QR on an NVIDIA A100 80GB GPU. The execution time of the decomposition was measured as a function of D for both cuTensorNet and an equivalent CPU-based (NumPy) implementation for comparison. All CPU performance results were completed with the same EPYC 7742 CPU, using all cores.
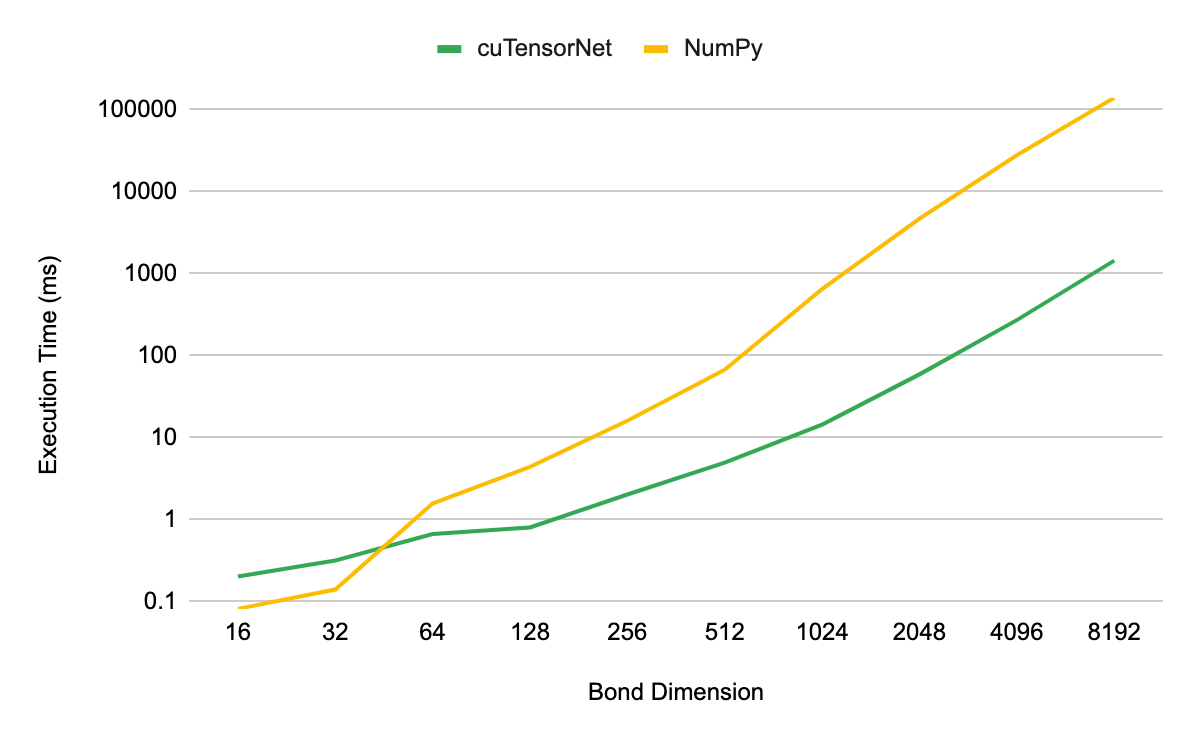
Figure 1 shows that cuTensorNet yields an order-of-magnitude speedup over a CPU-based NumPy implementation when using bond dimensions greater than 32. At a bond dimension of 8,192, you see speedups as high as 96x over the CPU implementation.
Tensor SVD
Tensor SVD has a definition and purpose similar to tensor QR, described earlier. The singular values from the decomposition contain important information about the quantum systems. For instance, the singular values of the quantum states are directly related to the Von Neumann entanglement entropy of the underlying quantum circuit. For weakly to intermediate-entangled quantum systems, the tails of the singular values can be truncated in order to reduce computational cost while maintaining high accuracy within the simulation.
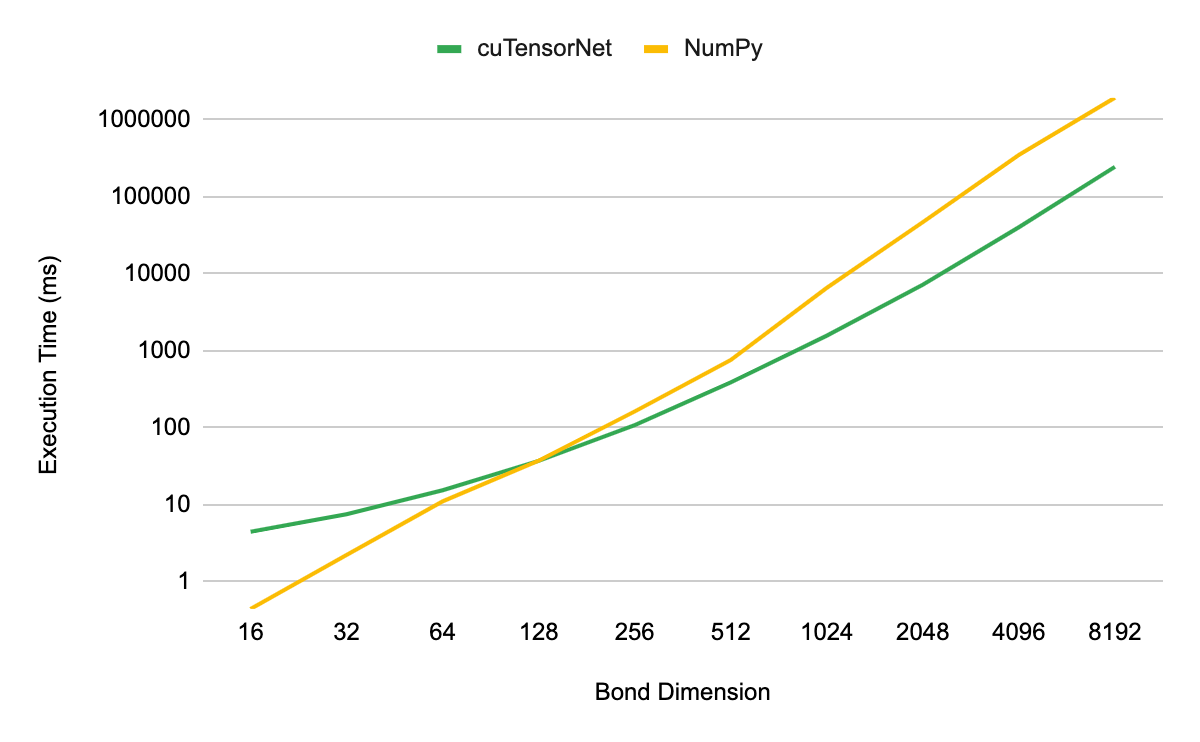
Tensor SVD performance is measured in the same manner as tensor QR. We find that when simulating bonds of dimension greater than 128, the cuTensorNet implementation provides a performance advantage. When scaling up to 8,192 dimensions, we see a 7.5x speedup.
Transforming a quantum circuit into an MPS representation
In the quantum circuit model, when a 2-qubit gate operand is applied to a pair of connected tensors, you can perform a sequence of operations to absorb the gate onto the two connected tensors while maintaining a fixed topology.
This type of operation forms the basis for constructing an MPS or PEPS representation of the quantum circuit. Truncation can be included as part of the process when performing tensor SVD to keep the computational cost tractable. For instance, an approximate MPS simulation of a quantum circuit can be achieved by iteratively using this technique on all 2-qubit gates (Figure 3).
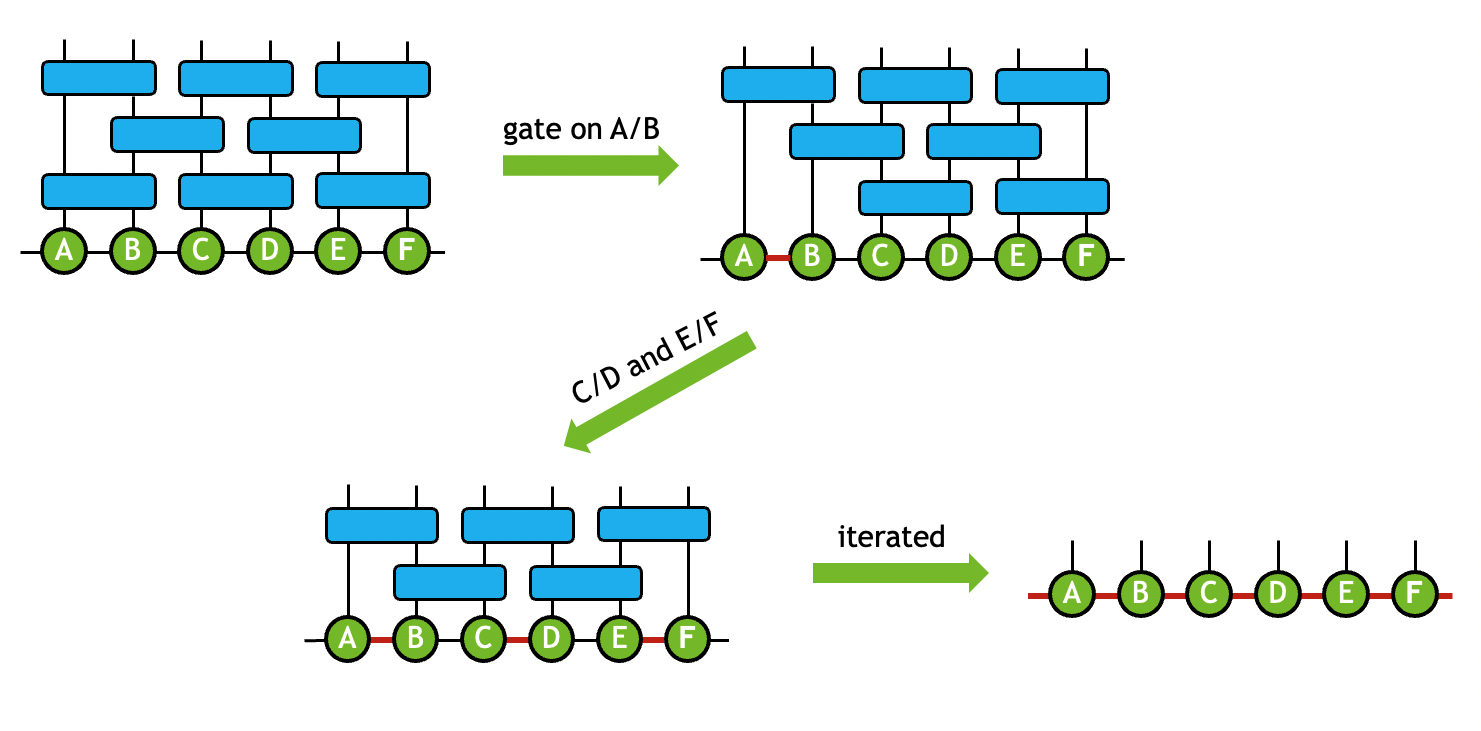
Tensor networks can be simplified by absorbing 2-qubit gates onto the connected tensors through the gate split function. By iterating through this process, an MPS is generated, which can then be contracted in order to simulate quantum circuits. This reduces the complexity of the network connectivity and is the cornerstone of value behind MPS quantum circuit simulations. You can leverage truncated tensor SVD to further reduce the network size and computational cost. After iterating through this process many times, you are left with an MPS that can be contracted to simulate quantum circuit operations.
Gate split
The final component necessary to implement quantum circuit simulations with approximate tensor network methods using cuTensorNet is the gate split functionality introduced in version 2.0.0. The team provides samples that show how to best use each of these components on their own in the cuQuantum GitHub repo, in addition to a specific sample that uses them all to implement MPS quantum simulations.
The performance of this function was tested by examining the execution time for the last and most costly step in constructing the final MPS as a function of bond dimension. When scaling beyond bond dimensions of 128, you can begin to see the advantages of leveraging GPUs for MPS simulations.
At a bond dimension of 8,192, a speedup of roughly 7.8x is observed for cuTensorNet on an NVIDIA A100 80GB GPU compared to the standard NumPy implementation on the same Data Center Grade CPU.
Getting started with cuTensorNet for quantum simulation
cuTensorNet v2.0.0 is available today. You can access it through conda-forge, pip, or cuQuantum installers. To get started on the new features quickly, see Approximation Setting: SVD Options. For a detailed guide, see the code samples. To request features or report bugs, reach out to NVIDIA/cuQuantum on GitHub.
For more information, see the following quantum computing resources: