在之前关于 FP8 训练的博文中,我们探讨了 FP8 精度的基础知识 并深入分析了适用于大规模深度学习的 多种扩展方法。如果您尚未阅读这些内容,建议您从该博文入手,以建立扎实的基础。
本文重点探讨生产环境中至关重要的因素:速度。FP8 训练有望提升计算速度,但在现实场景中究竟能实现多大程度的加速?此外,还有哪些潜在的间接开销可能削弱这些理论上的收益?
我们将使用 NVIDIA H100 和 NVIDIA DGX B200 GPU 上的真实基准,对领先的 FP8 扩展方案进行并排比较。通过 NVIDIA NeMo 框架,我们从训练效率、数值稳定性、硬件兼容性以及模型规模增大时的可扩展性等方面,全面评估每种 FP8 配方在延迟和当前扩展至 MXFP8 及通用块扩展方面的表现。
通过研究不同大语言模型(LLM)的token行为和吞吐量,本文将为各类方法在要求严苛的实际场景中的表现提供清晰且可行的见解。
为什么加速在 FP8 训练中很重要?
训练大型语言模型(LLM)和其他先进的神经网络正成为一个日益耗费资源的过程,需要巨大的计算能力、内存和时间。随着模型和数据集规模的持续扩大,相关的成本(包括财务、环境和时间成本)已成为研究人员和从业者关注的核心问题。
FP8 精度通过从根本上提升计算效率,直接应对了这些挑战。通过将数字精度从 16 或 32 位降低至仅 8 位,FP8 能够显著加快计算速度,从而加速研究周期、降低基础设施支出,并在现有硬件上训练更大、更具雄心的模型。
除了原始计算速度之外,FP8 还能显著降低分布式训练环境中的通信开销。由于较低精度的激活值和梯度意味着在 GPU 之间需要传输的数据量更少,从而有效缓解通信瓶颈,有助于维持大规模训练时的高吞吐量。随着模型和集群规模的不断扩大,这一优势愈发显著。
FP8 扩展方法有哪些优势和权衡取舍?
本节将简要回顾本研究中评估的四种主要 FP8 扩展方法,并突出其独特特征。如需深入了解各方法的机制与实现细节,请参阅有效 FP8 训练的按 tensor 和按块扩展策略。
- 按张量延迟扩展: 通过使用由历史记录衍生的稳定扩展因子,提供良好的 FP8 计算性能,但其鲁棒性可能会受到 Amax 历史记录中异常值的影响,可能会导致不稳定并阻碍整体训练。
- 按张量电流扩展: 提供高响应速度和对张量范围的即时适应,从而改进模型收,并保持最小的计算和内存用度,因为它具有实时 Amax 计算和缺乏历史跟踪。
- 子通道 (通用块) 扩展: 通过允许可配置的块维度和更细粒度的扩展,提高精度并充分释放 FP8 效率,但较小的块会增加扩展因子存储开销,并且转置操作可能涉及重新计算。
- MXFP8: 作为一种硬件原生解决方案,此 recipe 使用固定的 32 值块为激活函数和权重以及 E8M0 的 2 倍功率扩展提供高效的块扩展,从而显著提高性能 (高达 2 倍的 GEMM 吞吐量) ,并通过 NVIDIA Blackwell 加速运算更大限度地减少量化错误。
| 扩展方法 | 加速 | 数值稳定性 | 粒度 | 推荐模型 | 推荐的硬件 |
| 延迟扩展 | 高 | 适中 | 每张量 | 小型密集模型 | NVIDIA Hopper |
| 当前扩展 | 高 | 高 | 每张量 | 中型密集模型和混合模型 | NVIDIA Hopper |
| 子通道扩展 | 中型 | 高 | 自定义 128 × 128 的 2D 块 | MoE 模型 | NVIDIA Hopper 和 Blackwell |
| MXFP8 | 中型 | 高 | 每 32 值块 | 所有 | NVIDIA Blackwell 和 Grace-Blackwell |
扩大配方粒度
图1展示了在NVIDIA H100上,各种扩展方法相对于BF16测得的FP8高精度矩阵乘法(GEMM)吞吐量的加速情况。硬件原生扩展(包括通道级、子通道级和张量级)可实现高达2倍的加速,这凸显了FP8在硬件层面高效的原因。
尽管与 BF16 相比,FP8 能够带来显著的加速效果,但缩放粒度的选择——具体体现在如何在张量内部应用细粒度的缩放因子——在实际性能中引入了微妙的权衡,尤其是在 GEMM 运算中。更细的粒度有助于更好地适应张量内部的数值变化,提升数值稳定性和精度,但同时也会带来额外的开销,从而影响整体吞吐量。
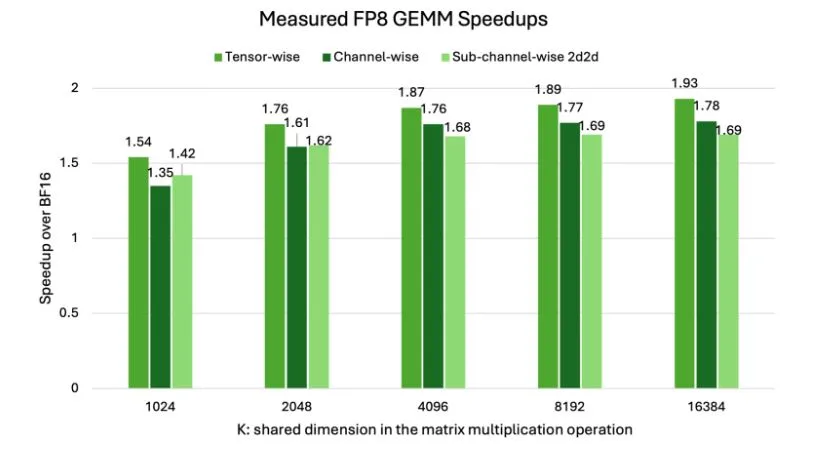
当 GEMM 运算的缩放粒度发生变化时,性能的层次结构清晰显现。张量级缩放通常表现出最高加速效果。由于 GEMM 中每个完整张量仅涉及一个扩展系数,因此与扩展管理相关的开销被降至最低。
通道级缩放 表示一种中等粒度的方法,通常为每个通道或行/列应用缩放系数。如图所示,其加速效果介于张量级和 2D 块级方法之间。
次通道 2D2D 缩放(例如,采用 1 = 128 的激活函数和 128 = 128 的权重块)实现了更精细的粒度,与张量缩放相比,通常会带来略低的加速效果。管理张量内大量较小块的多个扩展因子会引入额外的计算开销,尽管这对保持精度至关重要,但可能会影响峰值原始吞吐量。其他可配置的块维度(如 1D1D 或 1D2D)也存在类似情况,其中更细粒度的块划分会导致每次 GEMM 运算的处理规模增大。
至关重要的是,图 1 中的 x 轴突出了 GEMM 大小的影响。随着 K 值的增加(意味着更大的 GEMM 运算),FP8 在所有扩展方法中相较于 BF16 的整体加速通常会进一步提升。这是因为对于较大的 GEMM 运算而言,采用 8 位精度所带来的计算量节省更加显著,从而超过了管理扩展因子所带来的相对开销。本质上,更大的 GEMM 能够更充分地发挥 FP8 计算的固有优势,即使细粒度扩展的复杂性随之增加。
尽管 MXFP8 等硬件原生解决方案通过专用的 Tensor Core 加速来降低块扩展的开销,但在通用 FP8 块扩展实现中,精度粒度与原始性能之间的权衡仍是一个关键考量。
除了原始加速之外,低精度训练的一个关键方面是收敛,即模型如何学习并减少损失,以及最终如何执行特定的下游任务。虽然训练损失可以为学习过程提供宝贵的见解,但需注意,它并非衡量 FP8 有效性的唯一指标;可靠的 FP8 下游评估指标才是模型质量的最终决定因素。
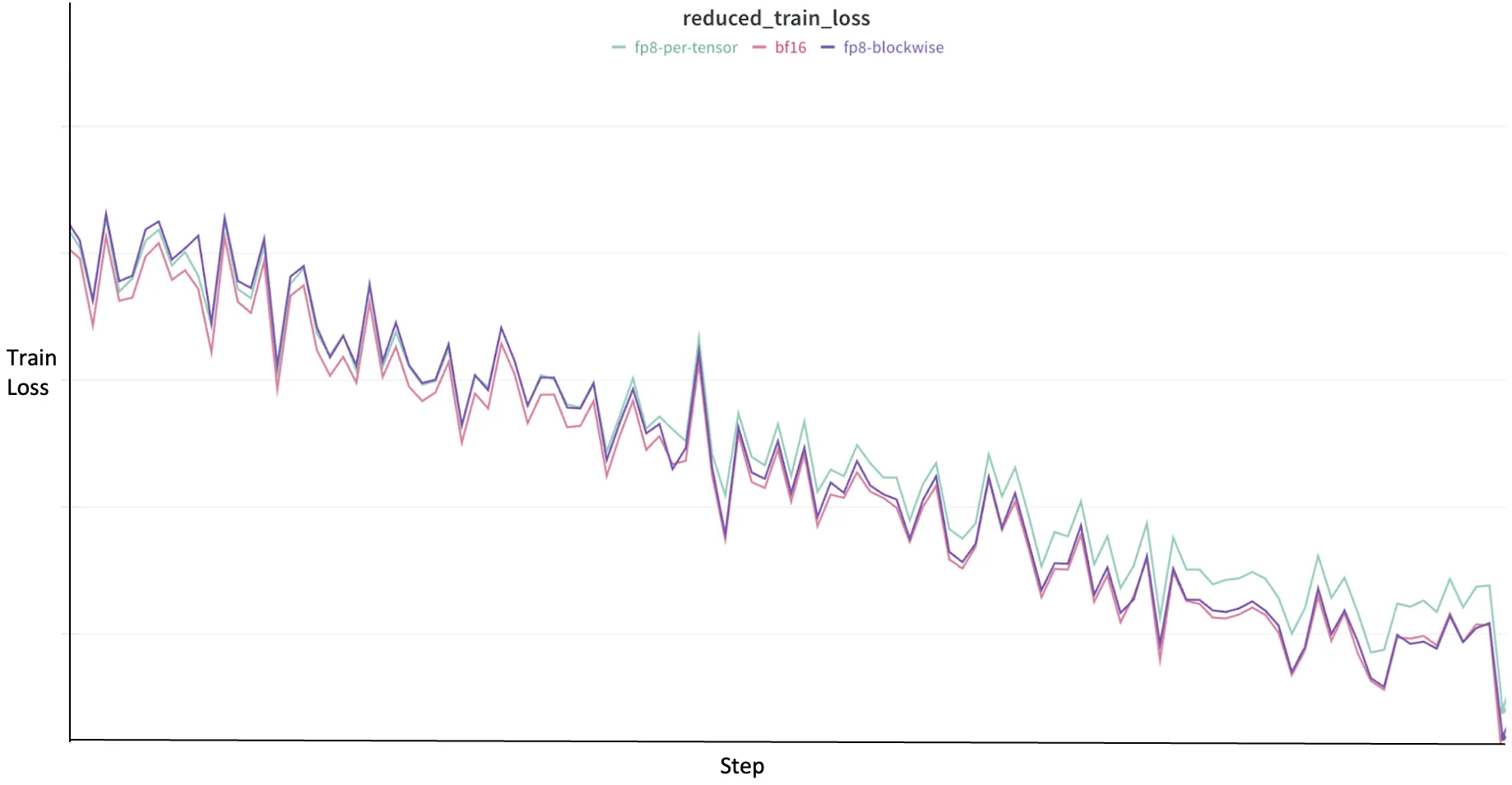
采用 FP8 时,预期训练损失轨迹应与更高精度基准(例如 BF16)的轨迹高度一致,以确保模型在有效学习的同时不会出现明显的性能下降。如图 2 所示,不同缩放策略的训练损失轨迹均相对于 BF16 进行比较,其中粉色线表示 BF16 基准。值得注意的是,深紫色线代表 FP8 块级缩放,其轨迹始终与 BF16 高度吻合。这种紧密的对齐表明,随着粒度的提升,块级缩放能够更有效地保持数值保真度,从而实现与高精度 BF16 训练相匹配的收敛行为。
相反,浅绿色线表示每个张量的 FP8 缩放,偶尔会表现出轻微的偏差或更高的损失波动。这种轨迹上的细微差异凸显了粒度所固有的权衡:正如之前所讨论的,粗粒度每张量缩放可能带来更高的原始 GEMM 吞吐量,而细粒度块缩放通常能实现更小的准确性损失和更稳定的学习路径,表现与 BF16 非常相似。
这说明了在 FP8 训练中,加速与数值稳定性之间需要实现关键的平衡。更精细的缩放方法能够更好地适应张量内部不同的动态范围,从而生成更忠实地追踪高精度基线的收敛轨迹;然而,与较简单的方法相比,这可能带来一定的速度差异。理想的选择通常需根据可用的计算资源、所需的训练速度,以及下游评估的要求进行权衡。
实验性设置
本文中的所有实验均使用 NVIDIA NeMo 框架 25.04,撰写本文时 NeMo 框架的最新版本完成。NeMo Framework 25.04 通过 NVIDIA Transformer Engine(TE) 为 FP8 训练提供可靠的生产级支持,并包含适用于密集架构的开箱即用方案。
我们评估了两种先进的 FP8 方法:一种是在 H100 GPU 上采用的当前扩展方案,另一种是基于较新的 NVIDIA DGX B200 架构的 MXFP8 方法。为此,我们测试了一系列前沿模型,包括 Llama 3 8B、Llama 3 70B、Llama 3.1 405B、Nemotron 15B 和 Nemotron 340B。所有测试配置均与 BF16 基准直接对比,以衡量 FP8 在实际训练场景中带来的加速效果。
当前扩展方法
如图 3 所示,与 BF16 基准相比,H100 GPU 上当前扩展的 FP8 方法表现出与模型规模相关的显著加速。对于 Llama3 8B 等较小的模型,加速比约为 1.30 倍。
这种优势在更大的架构中愈发显著。例如,Llama 3 70B 模型实现了 1.43 倍的加速,而在我们基准测试套件中规模最大的 Llama 3.1 405B 模型更是实现了 1.53 倍的惊人加速。
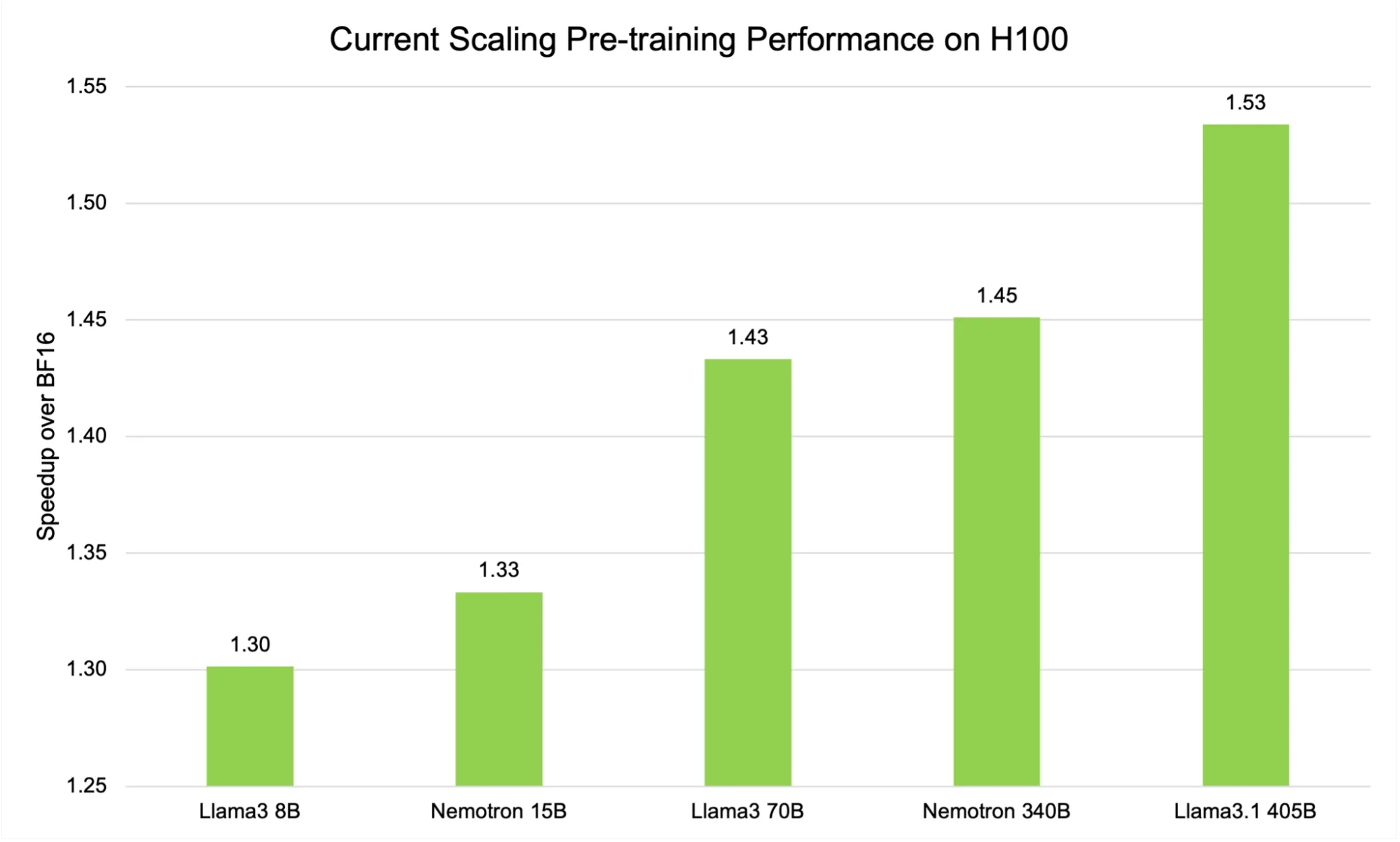
这种上升趋势不仅仅出于统计上的好奇,更凸显了FP8训练在大规模语言模型中的根本性优势。随着模型规模和计算复杂性的增加,通过降低精度算法所带来的效率提升也愈发显著。
原因有二:首先,较大的模型自然涉及更多的矩阵乘法和数据移动,这两项操作都能从现代硬件上 FP8 所带来的显存占用降低和更高吞吐量中显著受益。其次,随着总体计算量的增加,与扩展和动态范围调整相关的开销占比相对减小,从而使 FP8 的原始性能优势更加突出。
MXFP8 方法
图 4 展示了 MXFP8 Blueprint 在 DGX B200 GPU 上的性能表现,显示在不同模型规模下,与 BF16 相比,MXFP8 Blueprint 均实现了稳定的速度提升,观测到的加速比在 1.28 倍至 1.37 倍之间。尽管这些绝对加速效果略低于当前扩展方法所达到的水平,但其在多种模型中表现出的一致性和可靠性仍值得关注。
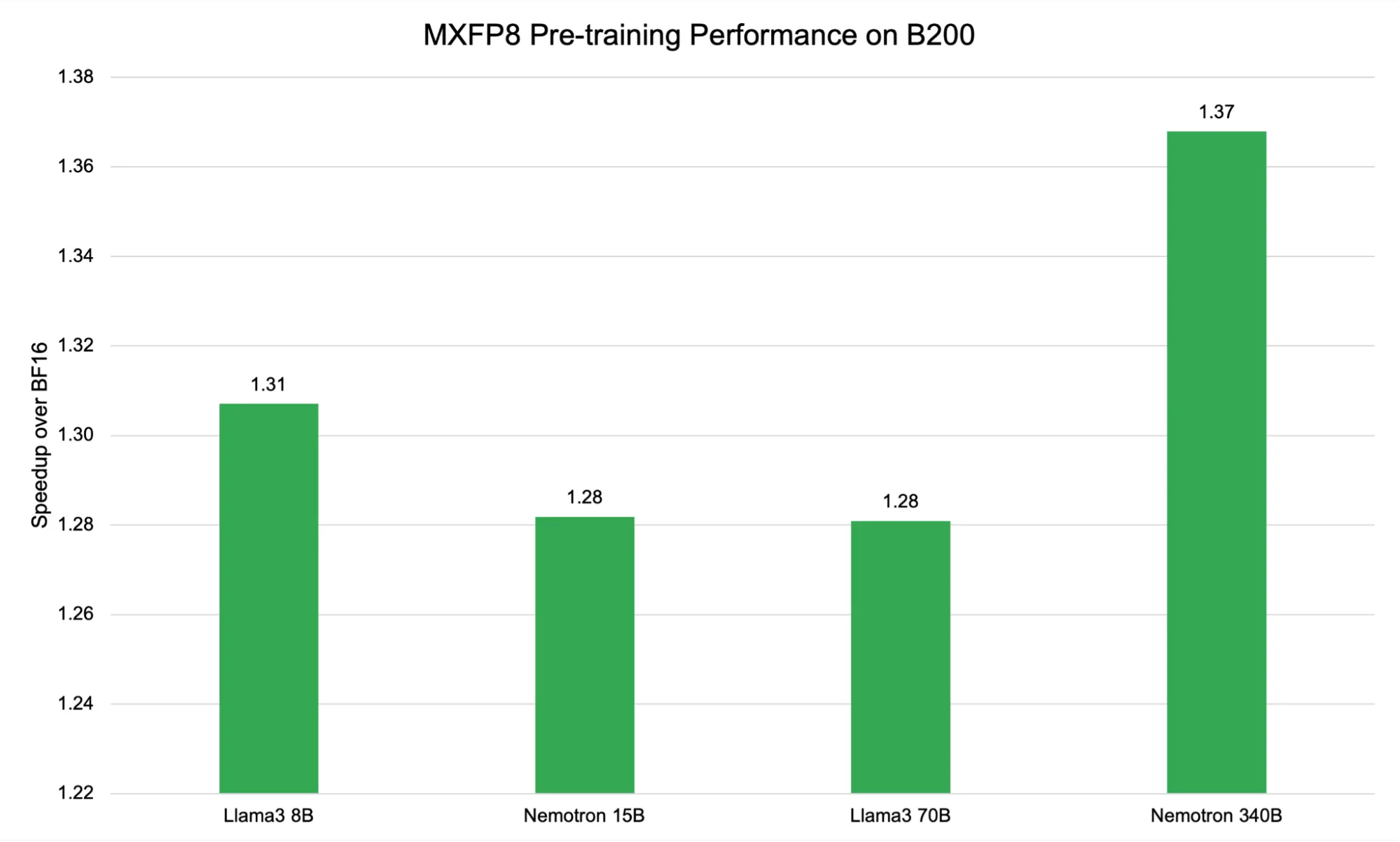
从 80 亿到 700 亿参数的扩展过程相对平稳(与 340B 时的较大跃升形成对比),反映了基于块的扩展方式与模型及硬件特性的相互作用。MXFP8 为每个 32 单元块分配一个共享的扩展系数,这可能为中等规模模型带来额外的内存访问开销。然而,随着模型规模的增大,计算逐渐成为主要瓶颈(如 Nemotron 340B 所示),此时块级 FP8 的效率优势愈发显著,从而带来了明显的峰值加速。
这些结果凸显了 Blackwell (B200) 平台的架构优势,其 Tensor Core 和内存层次结构针对 MXFP8 等微缩放大格式进行了优化。即使模型扩展到数千亿个参数,也能实现高吞吐量和稳定的收敛。MXFP8 的块级扩展方法可有效平衡动态范围与计算效率,在提供可靠加速的同时降低数值不稳定的风险。
这种一致性体现了 NVIDIA Blackwell 架构的显著进步,该架构旨在大幅提升 FP8 等低精度格式的效率,尤其优化了 MXFP8 等基于块的扩展方法的性能。B200 Tensor Core 与先进的内存层次结构均针对这些量化格式进行了专门设计,即使在模型规模持续增长的情况下,仍能实现高吞吐量和高效的内存利用。使用 MXFP8 时,每 32 个值组成的块共享一个缩放系数,从而在动态范围与计算效率之间取得良好平衡。这种方法不仅带来了显著的加速效果,同时有效降低了数值不稳定的风险,这对于推动模型向更大规模发展至关重要。
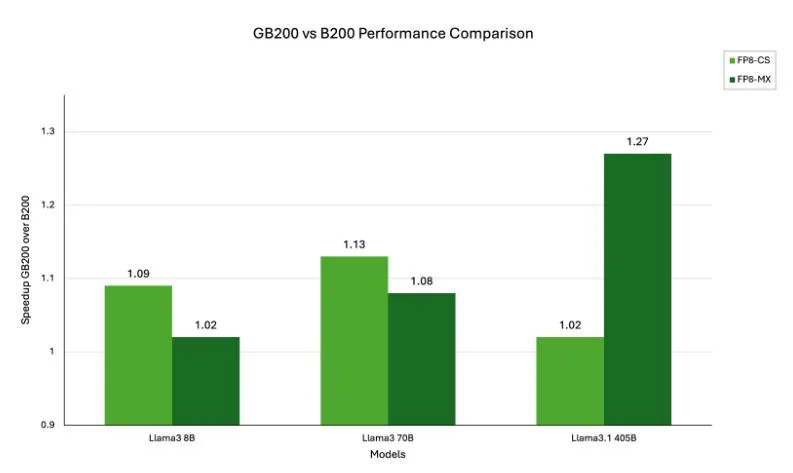
NVIDIA GB200 Grace Blackwell 超级芯片与 NVIDIA Blackwell 架构相比如何?
GB200 与 B200 的对比凸显了架构集成和系统设计如何为大规模 AI 工作负载带来显著的性能提升。两者均基于 NVIDIA Blackwell 架构构建,但 GB200 超级芯片将两个 B200 GPU 与一个 Grace CPU 相结合,并通过 NVIDIA NVLink 实现互联,从而形成统一的内存域并提供极高的内存带宽。
开始实际的 FP8 训练
这些基准测试呈现出一个清晰的模式:对于密集模型而言,模型规模越大,FP8 带来的加速效果就越显著。这是因为随着模型规模的扩大,矩阵乘法(GEMM)的运算量迅速增加,而 FP8 所提供的较低精度和更高吞吐量恰好能最大程度地优化这类计算。在大型密集模型中,FP8 能够显著提升计算效率,从而使得训练和微调更大规模的语言模型所需的时间和计算资源更少。
这些实验结果进一步印证了本文详细阐述的每种 FP8 扩展方法的具体优势与权衡,并表明每张量和 MXFP8 方法相较于 BF16 在加速和收敛方面具有显著优势。
准备好亲自尝试这些技术了吗?深入了解 FP8 方法,并通过实用的训练配置和代码开始实践。





