NVIDIA Modulus was previously known as NVIDIA SimNet.
Simulations are pervasive in every domain of science and engineering, but they are often constrained by large computational times, limited compute resources, tedious manual setup efforts, and the need for technical expertise. NVIDIA Modulus is a simulation toolkit that addresses these challenges with a combination of AI and physics.
A success story of Modulus application today is in modeling the flow and transport in porous media. This effort was led by Cedric Frances, a PhD student at Stanford University.
Use case study
Cedric is researching the applicability and limitations of mesh-free reservoir simulations using physics-informed neural networks (PINNs). He’s keenly interested in the flow and transport problem in porous media (conservation of mass and Darcy flow). Cedric’s application is a Python-based reservoir simulator, which computes the pressure and concentrations of various fluids in a porous media and enables predictions that typically affect large, industrial energy projects. This includes the production of hydrocarbons, storage of carbon dioxide, water disposal, air storage, waste management, and so on.
Researchers previously tried to use the PINNs approach to capture the solution of a hyperbolic problem with nonconvex flux term (Riemann problem) in a forward setting with no data other than initial and boundary conditions. Unfortunately, these attempts were unsuccessful.
Before trying out Modulus, Cedric developed his own implementations of PINNs using Python and deep learning frameworks such as TensorFlow and Keras. He used various architectures of networks, such as residual, GAN, periodic activation, CNN, PDE-Net, and so on. However, it was difficult to implement all of them to find which one worked best or worked at all. The emergence of open-source code on GitHub made it easy to test these implementations out. The high overhead involved in every new implementation, such as environment setup, hardware configuration, modification of code to test his own problem, and so on, was not efficient.
Cedric wanted to have a good, unified framework maintained by a team of professional software developers to solve problems that allowed him to focus on the physics of the problem and extensively test the methods that have been recently published. His search for such a framework ended when he stumbled upon Modulus.
Cedric downloaded Modulus and started using fully connected networks with tanh activation functions and spatial weighing of the loss function. He discovered that the Modulus general-purpose framework with multiple architectures and well-documented examples served as a good starting point. Its ability to emulate solutions with sharp shocks, introduce new dynamic constraints such as entropy and velocity saved him weeks of development. More importantly, it provided a quick turnaround on testing methods to determine their usefulness.
The problem presented here is that of incompressible, immiscible displacement of two phases in a porous medium. This is also referred to as transport problem and has been delineated in various forms over the years. It has been applied to the displacement of oil by water for waterflood problems in reservoir for over half a century. More recently, it’s been applied to the displacement of brine by CO2 in carbon sequestration applications. For more information, see Mechanism of Fluid Displacement in Sands and Theory of Gas Injection Processes.
Assume that a wetting phase (w) is displacing a nonwetting phase (n). Wettability is the preference of a fluid to be in contact with a solid surrounded by another fluid; for example, water is wetting on most surfaces compared to air. Conservation of mass applies to both phases. For the wetting phase:
(1)
In this formula, is the porosity,
is the saturation (or concentration) of that wetting phase, and is the saturation of the nonwetting. The flow rate of the wetting phase
can be written as follows:
(2)
In this formula, is the absolute permeability that quantifies the propensity of a material to allow liquid or gas to flow through it.
is the wetting phase relative permeability that is function of the saturation and characterizes the effective permeability of a given phase in the presence or absence of it. A phase preferentially flows through a path where it is already present. Think of a drop of water dripping down from a window and following existing trails.
You can formulate the phase flux of the wetting phase as a function of the total flux
using a simple homogenization rule:
(3)
You can rewrite this equation as a function of the total flux. This gives rise to the fractional flow:
(4)
The conservation equation can now be written:
(5)
For a one-dimensional case where you assume that the total flux is equal to one pore volume injected per time step (), you can obtain the equation:
(6)
In this formula, the fractional flow is a nonlinear equation defined as follows:
(7)
In this formula, and
are the residual (irreducible) saturations for the wetting and nonwettings resulting from trapping mechanisms and
is the endpoint mobility ratio defined as the ratio of endpoint-relative permeability and viscosity of both phases. We used the Corey and Brooks relative permeability relationship. For more information, see Hydraulic Properties of Porous Media.
The partial differential equation solved here is a hyperbolic of order 1 and the fractional flow term is nonconvex. It belongs to the class of Riemann conservation problem that is typically solved using finite volume methods. For more information, see Hyperbolic systems of conservation laws and the mathematical theory of shock waves.
With uniform Dirichlet boundary conditions:
(8)
(9)
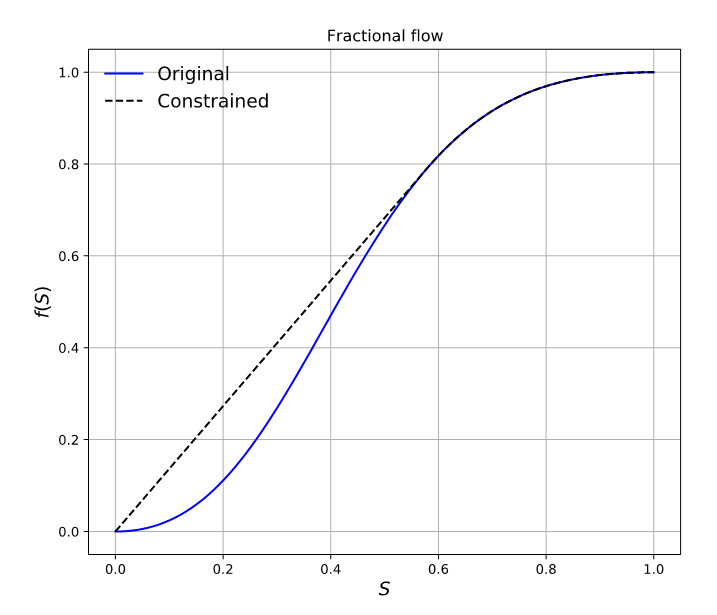
You can apply the method of characteristics (MOC) to build an analytical solution to this equation. For the MOC or any finite volume method to be conservative, you must modify the fractional flow term as shown in Figure 1.
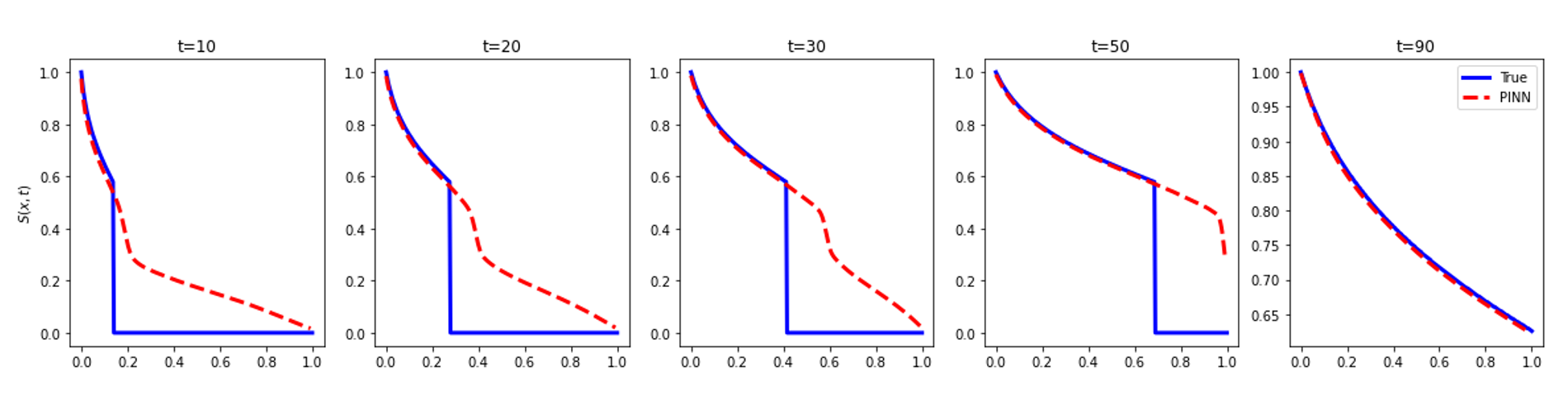
Until now, no other known method solved such a problem using a sampling method, so this remained an open question. A previous attempt by Fuks and Tchelepi concluded that physics-informed approaches were not suitable for the problem described (Figure 2).
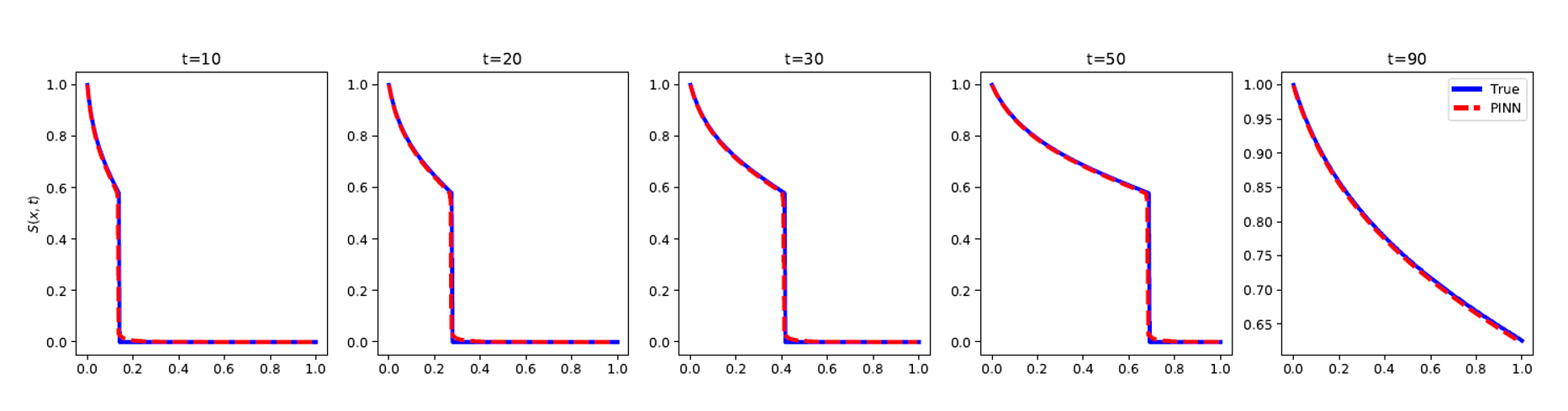
Cedric’s research on this topic has now been published: Physics Informed Deep Learning for Flow and Transport in Porous Media.
Important theoretical milestones are now being reached on simple yet challenging 1D examples. Cedric plans on expanding his study to larger dimensions (2D and 3D), where the scalability of the code and the easy deployment on larger arrays will be put to the test. He expects to encounter similar issues and is looking forward to the gain provided by Modulus going from 2D to 3D, for example.
Cedric elaborated on his experience with Modulus. “Modulus’s clear APIs, clean and easily navigable code, environment and hardware configurations well handled with Docker containers, scalability, ease of deployment and the competent support team made it easy to adopt and has provided some very promising results. This has been great so far and we look forward to using Modulus on problems with much larger dimensions.”
To view the GTC session, see Physics-Informed Neural Network for Flow and Transport in Porous Media. For more information about features and to download the toolkit, see NVIDIA Modulus.