NVIDIA Modulus was previously known as NVIDIA SimNet.
An article in the latest edition of Science magazine, Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations, describes an emerging branch of fluid dynamics at the intersection of scientific computing and deep learning. It starts with imaging data and discovers the underlying physics and properties of the fluid using the partial differential equations (PDEs) describing the flow behavior. This method, called inverse approach, is used for predicting the flow velocities and pressures for the entire transient range without directly measuring them. It promises advances for a wide range of applications from preventing strokes to oil and gas exploration studies.
Another approach to AI can accurately predict phenomena, such as lift and drag forces in aerodynamics, or the temperature and pressure drop in cooling of electronic devices. It involves forward solution of the PDEs for the underlying physics. This is different from the data driven approach used by standard neural networks that need a large number of datasets for learning.
NVIDIA is already using physics-informed neural networks (PINNs) in NVIDIA Modulus, architected for problems requiring either inverse approach or forward solution like traditional numerical solvers with use cases such as the design of heat sinks for its DGX Systems powered by the revolutionary NVIDIA Volta GPU platform. These networks require no data, can work with single or parameterized geometries and solve single or multi-physics problems. At the backend, NVIDIA GPUs are used for both training and inference, with the cuDNN-accelerated TensorFlow deep learning framework.
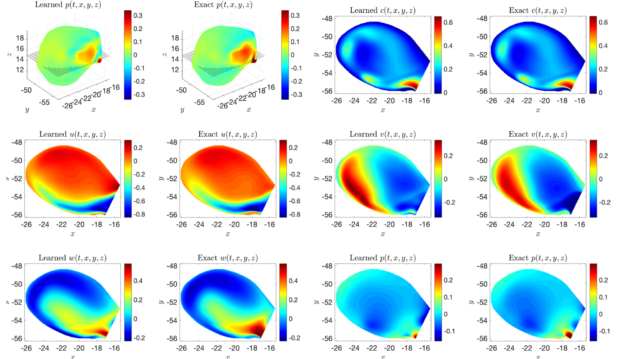
The inverse approach in Modulus has its roots in the work done at Brown University and was first outlined in Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations, on Science. For any kind of simulation, validation and verification are important for analysis to be trustworthy.
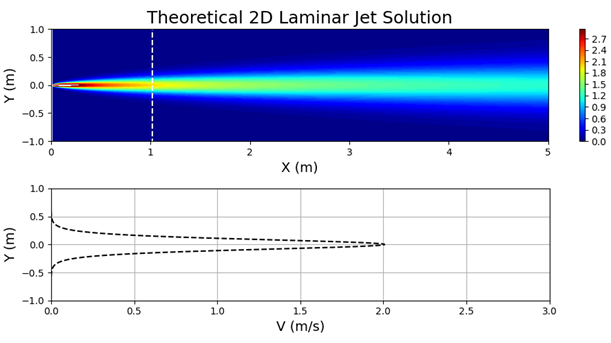
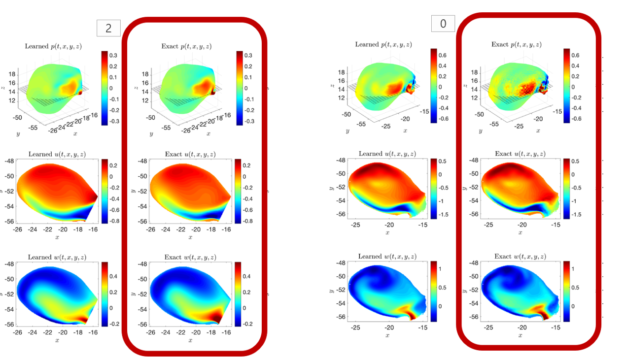
For the flow in an intracranial cerebral aneurysm, the predicted velocities and pressures using the physics-driven neural networks (called learned) are in the same range as the results using a traditional open source CFD solver (called exact) as shown in Figure 1.
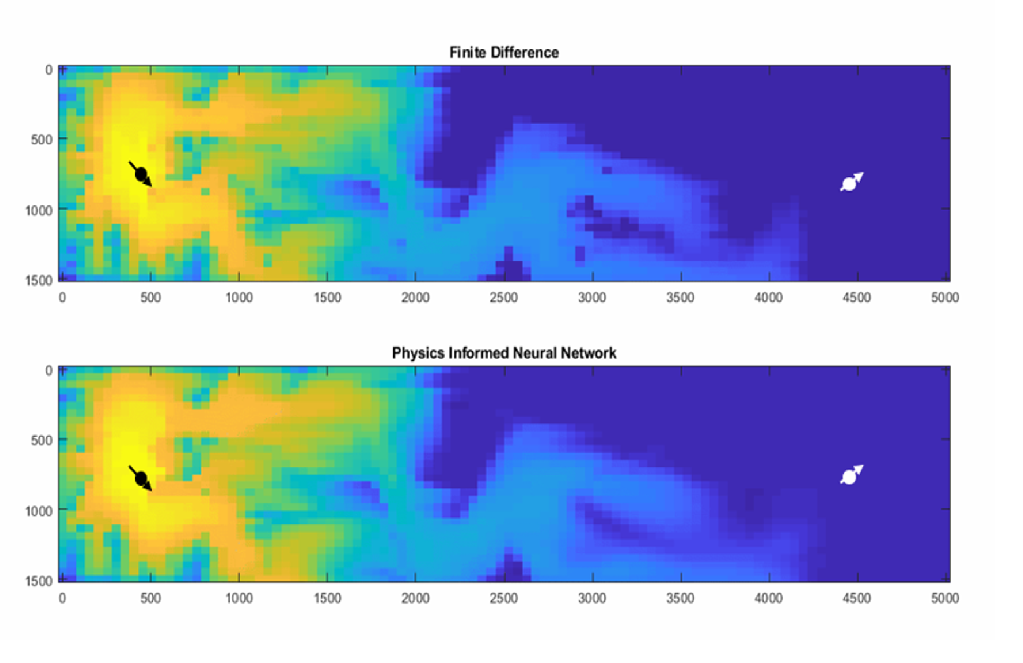
It is worth mentioning that two different CFD solvers can yield different results for the same use case due to different discretization schemes and numerical algorithms. In fact, even the same solver with two different users can yield different results. Therefore, it is reasonable to expect that the neural network results would be similar to the traditional solvers but not exactly the same. This is demonstrated in Figure. 2, where Modulus results are compared to two different open source CFD solvers. The Modulus results have a closer correlation with the CFD solver that uses the spectral h/p method than with the one using finite volume method.
As an extension of the current work in non-Newtonian fluids, the neural networks could also discover the relationship between the viscosity and shear strain rate. The resulting neural network could then be called from within the solver instead of using the existing empirical functions like the Carreau or Casson models.
Companies such as HeartFlow are already reviewing the techniques to see how they can leverage them. The startup, part of the NVIDIA Inception program, uses AI in a noninvasive alternative to angiograms to help physicians diagnose and treat coronary heart disease.
From heart attacks to heat sinks
As mentioned earlier, the inverse approach takes advantage of some measured sensor output, acoustic, or imaging data for the neural networks to discover the physics using relevant PDEs. However, many use cases may not have any measured data. In such cases, you would do forward simulations for multiple parameters or geometries to examine the best design.
NVIDIA engineers have extended Modulus for forward solution of parameterized, multiphysics problems. Starting with only the geometry and other physical parameters like material properties, boundary conditions, and so on, Modulus evaluates the entire range of possibilities just like the traditional solver would.
However, the big difference is while the traditional solver would require a separate run for each design, the neural networks can address the various different designs in one training cycle. After the network is trained, the individual design can be evaluated through inference, which computes in nearly real time. This approach holds advantage over both data-driven neural networks that require lots of data and do not generalize well, as well as traditional solvers, which are computationally expensive.
For the engineering physics problems, there are several considerations for the neural networks that must be accounted for in the neural network architecture:
- Sampling insensitivity
- Impact of the order of derivatives on the network structure
- Weighting the various PDEs for loss convergence acceleration
- Activation functions that do not reduce down to constants or vanish when differentiated
- Gradients and discontinuities due to geometrical effects
- Considerations of local compared to global mass balance equations
Standard networks that are driven by the data alone are grossly inadequate for modeling physics on various geometries.
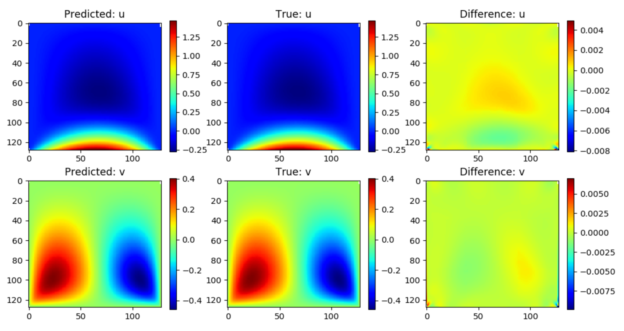
For validation, a forward solution of a lid-driven cavity was evaluated using Modulus. As shown in Figure 3, Modulus results compare well with a traditional solver with errors in the u and v components of velocity being 0.2% and 0.4%, respectively.
Modulus is used to improve the design and effectiveness of heat sinks where thousands of configurations can be analyzed within hours as opposed to weeks with the traditional simulations.

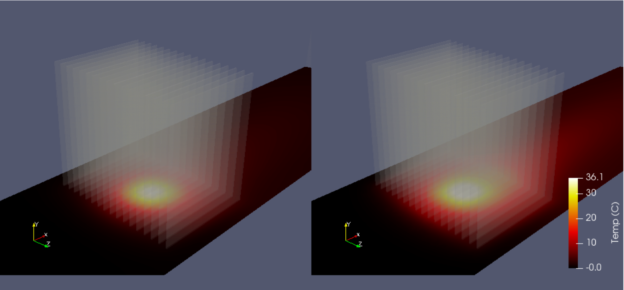
Figures 4A and B show good agreement of Modulus results with the traditional solver using conjugate heat transfer.
Next, Modulus is used for the design optimization of heat sinks where the minimum value on the temperature surface (red and yellow) is chosen for a given value on the pressure drop surface (blue) as shown in Figure 5.


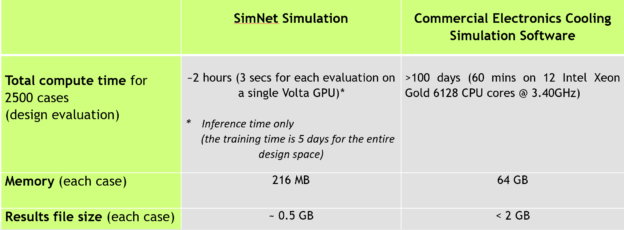
As shown in Table 1, even 50 dimensional variations for each of the two parameters, edge fin height and center fin height, result in 2500 design evaluations. The computational time for the traditional simulations is intractable, but the neural networks offer the possibility to analyze a full spectrum of designs.
NVIDIA CEO Jensen Huang demonstrated the work in a talk at the SC19 supercomputing conference in November. “It has the potential to simulate much larger models and do so more accurately” than current techniques, said Huang.