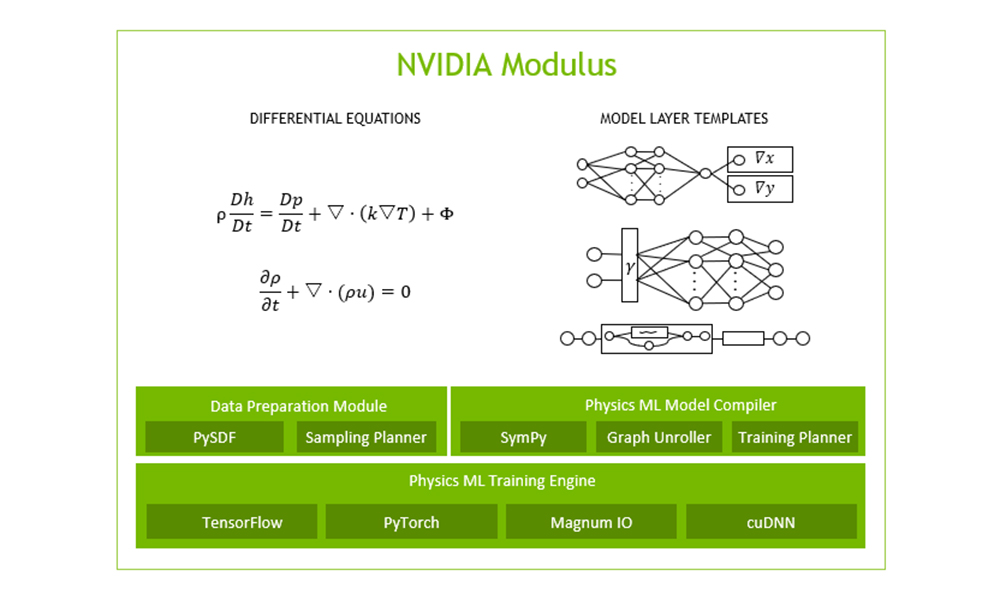
NVIDIA Modulus was previously known as NVIDIA SimNet.
NVIDIA recently announced the release of Modulus v20.12 with support for new physics such as fluid mechanics, linear elasticity and conductive as well as convective heat transfer. Systems governed by ordinary differential equations (ODEs) as well as partial differential equations (PDEs) can now be solved.
Previously announced in September, NVIDIA Modulus is a physics-informed neural network (PINN) toolkit for students and researchers who are either looking to get started with AI-driven physics simulations or are looking to leverage a powerful framework to implement their domain knowledge to solve complex nonlinear physics problems with real-world applications.
Modulus v20.12 highlights
Here are some highlights of the new Modulus release.
Multi-parameter training of complex geometries and physics
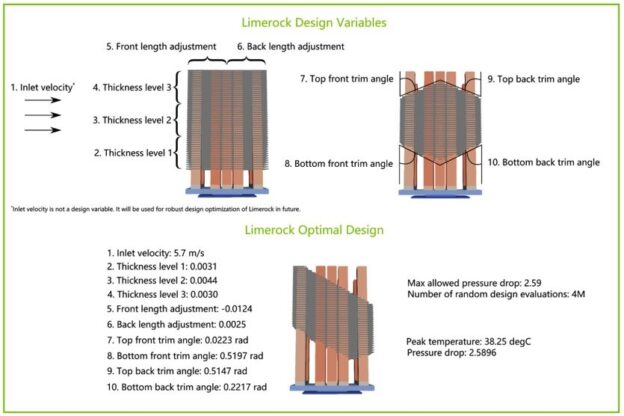
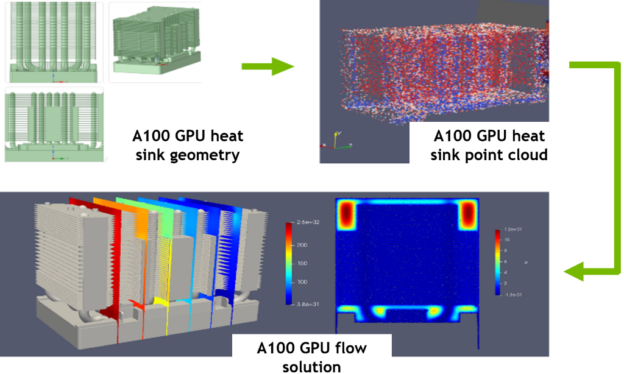
As a result of enhancements in network architectures as well as performance improvements, Modulus v20.12 converges to a lower loss faster. This enables training on several parameters in a single run. For a 10-parameter Limerock, training and inference for 59,049 configurations (three values for each design parameter) took 1000 V100 GPU hours. For same number of solver runs, the solver would take over 18.4 million hours (with 26 hours/configuration for a 12-core workstation).
Linear elasticity in solids
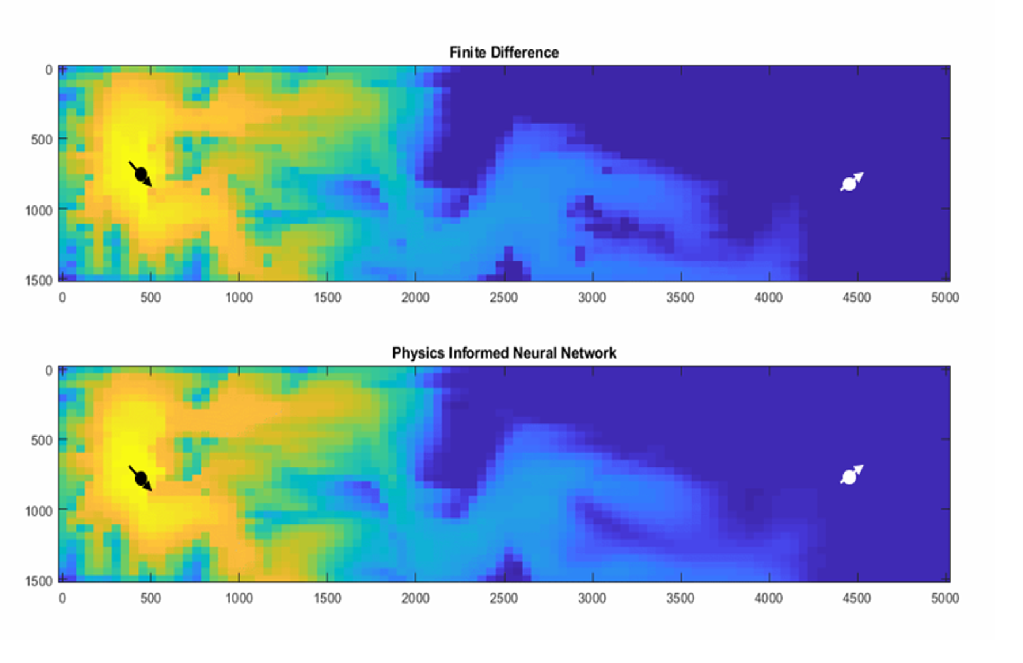
Linear elastic solid deformation is now included in the release in both Navier-Cauchy as well as Equilibrium forms. The solution has good agreement with finite element results.
The stresses from the linear elasticity formulation from Modulus were used in a digital twin model, developed by University of Central Florida, using RNN to model fatigue crack growth in an aircraft panel.

Improved STL geometry library
The PySDF library for STL geometries has been enhanced for about 10x more performance with better accuracy for complex geometries.
Integral form of partial differential equations
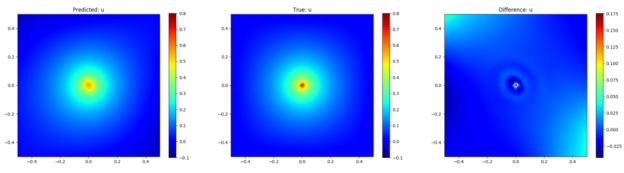
Some physics problems have no classical PDE (or strong) form but only a variational (or weak) form. This requires handling the PDEs in a different approach other than its original (classical) form, especially for interface problem, concave domain, singular problem, and so on. In Modulus, the PDEs can be solved not only in their strong form, but also in their weak form.

For example, a point source represented by delta Dirac function cannot be solved by the differential equations based PINNs but an integral form can capture the singular behavior at the center.
Strong scaling performance
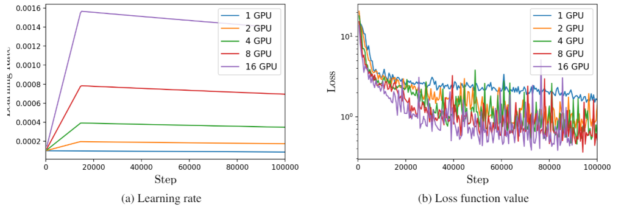
For the multi-GPU cases, the learning rate is gradually increased from the baseline case and this enables the model to train without diverging early on and enables the model to converge faster as a result of the increased global batch size coupled with the increased learning rate. The loss function evolution as the number of GPUs is increased from 1 to 16 for the NVSwitch heat sink case shows a progressive scaling from 2x for the 2-GPU case to 8x for the 16-GPU case.
Modulus in other news and events
- At PHM Society 2020, NVIDIA collaborated with the University of Central Florida (UCF) to solve the use case of a digital twin of aircraft cabin panels using Modulus. This was published in the PHM Society event.
- At SC20, we showcased how Modulus can help medical researchers simulate and predict the underlying blood flow physics in an aneurysm: SC20 Demo: Flow Physics Quantification in an Aneurysm Using NVIDIA Modulus.
- Read the paper, NVIDIA SimNet: an AI-accelerated multiphysics simulation framework.
Give it a try by requesting Modulus access today.