Modeling Earth’s Atmosphere with Spherical Fourier Neural Operators

Machine learning-based weather prediction has emerged as a promising complement to traditional numerical weather prediction (NWP) models. Models such as NVIDIA FourCastNet have demonstrated that the computational time for generating weather forecasts can be reduced from hours to mere seconds, a significant improvement to current NWP-based workflows.

Traditional methods are formulated from first principles and typically require a timestep restriction to guarantee the accuracy of the underlying numerical method. ML-based approaches do not come with such restrictions, and their uniform memory access patterns are ideally suited for GPUs.

However, these methods are purely data-driven, and you may rightfully ask:

How can we trust these models?
How well do they generalize?
How can we further increase their skill, trustworthiness, and explainability, if they are not formulated from first principles?

In this post, we discuss spherical Fourier neural operators (SFNOs), physical systems on the sphere, the importance of symmetries, and how SFNOs are implemented using the spherical harmonic transform (SHT). For more information about the math, see the ICML paper, Spherical Fourier Neural Operators: Learning Stable Dynamics on the Sphere.

The importance of symmetries

A video depicting two spherical plots, comparing a 5 month roll-out using SFNO to ground-truth data. — *Figure 1. 5-month-long rollout of SFNO. Surface windspeed predictions with SFNO and ground truth data are compared to each other.*

A potential approach to creating principled and trustworthy models involves formulating them in a manner akin to the formulation of physical laws.

Physical laws are typically formulated from symmetry considerations:

We do not expect physics to depend on the frame of reference.
We further expect underlying physical laws to remain unchanged if the frame of reference is altered.

In the context of physical systems on the sphere, changes in the frame of reference are accomplished through rotations. Thus, we strive to establish a formulation that remains equivariant under rotations.

Current ML-based weather prediction models treat the state of the atmosphere as a discrete series of vectors representing physical quantities of interest at various spatial locations over time. Any of these vectors are updated by a learned function, which maps the current state to the next state in the sequence.

In plain terms, we ask a neural network to consecutively predict the weather in the next time step when showing it the weather of today. This is comparable to the integration of a physical system using traditional methods, with the caveat of having learned the dynamics in a purely data-driven manner, as opposed to deriving them from physical laws. This approach enables significantly larger time steps as opposed to traditional methods.

The task at hand can thus be understood as learning image-to-image mappings between finite-dimensional vector spaces.

While a broad variety of neural network topologies such as U-Nets are applicable to this task, such approaches ignore the functional nature of the problem. Both input and output are functions and their evolution is governed by partial differential equations.

Traditional ML approaches such as U-Nets ignore this, as they learn a map at a fixed resolution. Neural operators generalize neural networks to solve this problem. Rather than learning maps between finite-dimensional spaces, they learn an operator that can directly map one function to another.

As such, Fourier neural operators (FNOs) provide a powerful framework for learning maps between function spaces and approximating the solution operator of PDEs, which maps one state to the next.

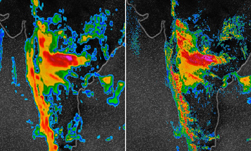
However, classical FNOs are defined in Cartesian space, whose associated symmetries differ from those of the sphere. In practice, ignoring the geometry and pretending that Earth is a periodic rectangle leads to artifacts, which accumulate on long rollouts, due to the autoregressive nature of the model. Such artifacts typically occur around the poles and lead to a breakdown of the model (Figure 2).

You may now wonder, what would an FNO on a sphere look like?

GIF shows two spherical plots, comparing polar artifacts of AFNO to SFNO. Artifacts are not present with SFNO, while AFNO shows artifacts rapidly accumulating. — *Figure 2. Temperature predictions using AFNO vs. SFNO*

Figure 2 shows temperature predictions using adaptive Fourier neural operators (AFNO) as compared to spherical Fourier neural operators (SFNO). Respecting the spherical geometry and associated symmetries avoids artifacts and enables a stable rollout.

Spherical Fourier neural operators

To respect the spherical geometry of Earth, we implemented spherical Fourier neural operators (SFNOs), a Fourier neural operator that is directly formulated in spherical coordinates. To achieve this, we made use of a convolution theorem formulated on the sphere.

Global convolutions are the central building blocks of FNOs. Their computation through FFTs is enabled by the convolution theorem: a powerful mathematical tool that connects convolutions to the Fourier transform.

Similarly, a convolution theorem on the sphere connects spherical convolutions to the generalization of the Fourier transform on the sphere: the spherical harmonic transform (SHT).

Implementing differentiable spherical harmonic transforms

To enable the implementation of SFNOs, we required a differentiable SHT. To this end, we implemented torch-harmonics, a PyTorch library for differentiable SHTs. The library natively supports the computation of SHTs on single and multiple GPUs as well as CPUs, to enable scalable model parallelism. torch-harmonics can be installed easily by running the following command:

pip install torch-harmonics

torch-harmonics seamlessly integrates with PyTorch. The differentiable SHT can be easily integrated into any existing ML architecture as a module. To compute the SHT of a random function, run the following code example:

import torch
import torch_harmonics as th

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# parameters
nlat = 512
nlon = 2*nlat
batch_size = 32
signal = torch.randn(batch_size, nlat, nlon)

# create SHT instance
sht = th.RealSHT(nlat, nlon).to(device).float()

# execute transform
coeffs = sht(signal)

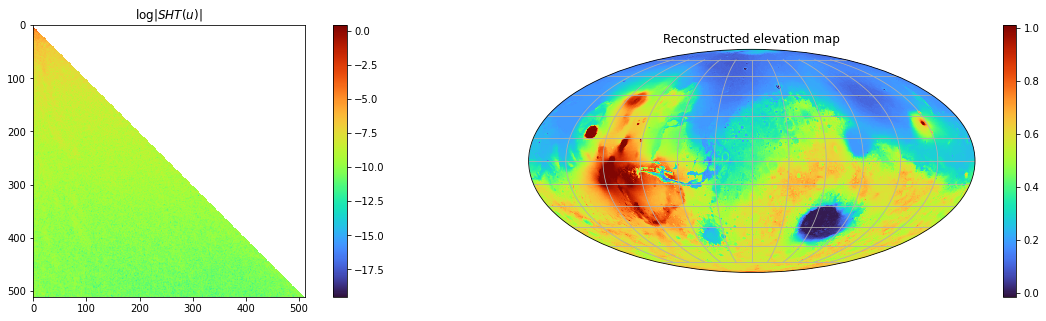
To get started with torch-harmonics, we recommend the getting-started notebook, which guides you through the computation of the spherical harmonic coefficients of Mars’ elevation map (Figure 3). The example showcases the computation of the coefficients using both the SHT and the differentiability of the ISHT.

Logarithmic chart depicting spherical harmonic coefficients next to an ellipsoid elevation map with color coding for elevation. — *Figure 3. Spherical harmonic coefficients of the elevation map of Mars, computed with torch-harmonics (left). Reconstructed signal computed with the inverse spherical harmonic transform (right).*

Implications for ML-based weather forecasting

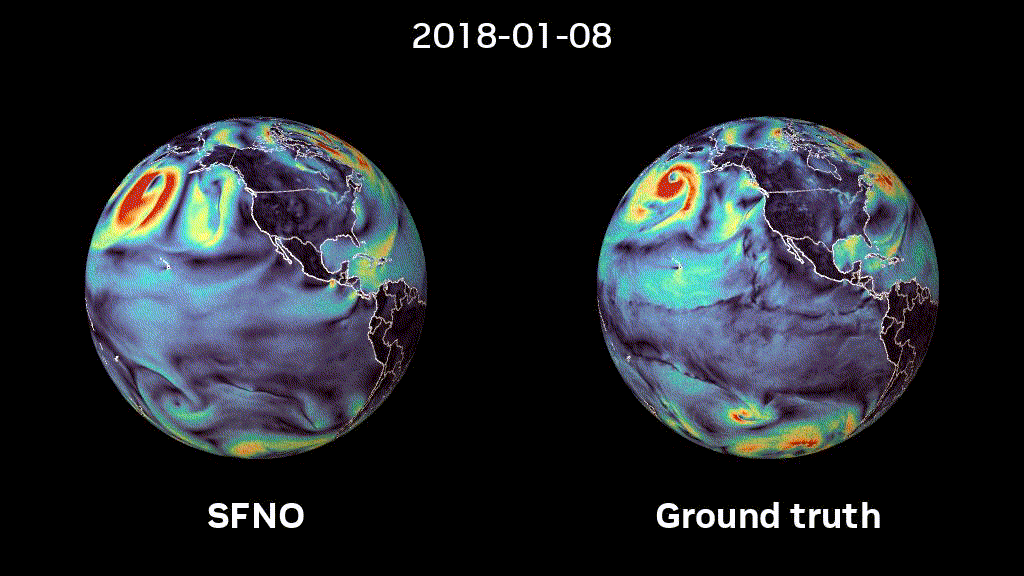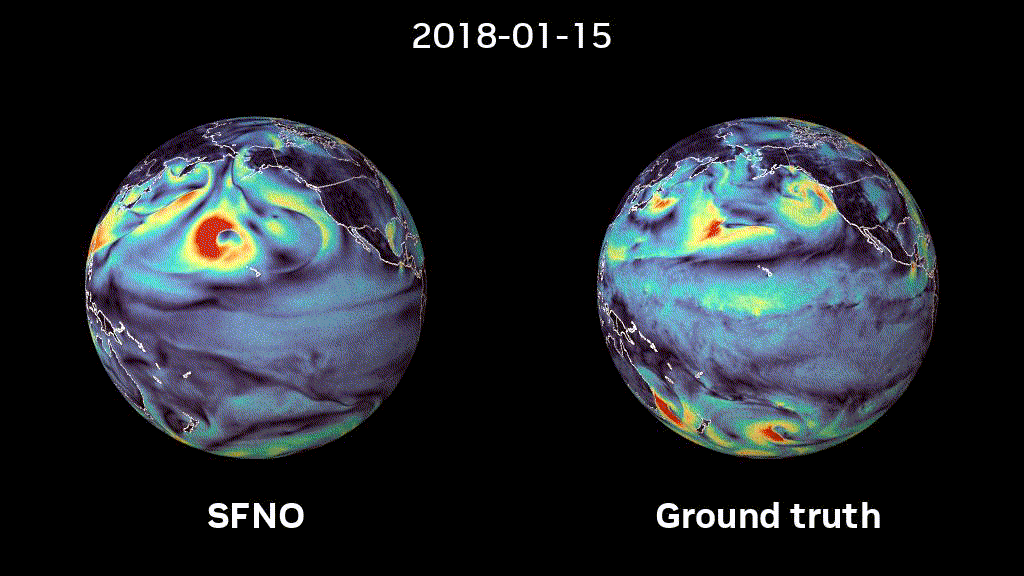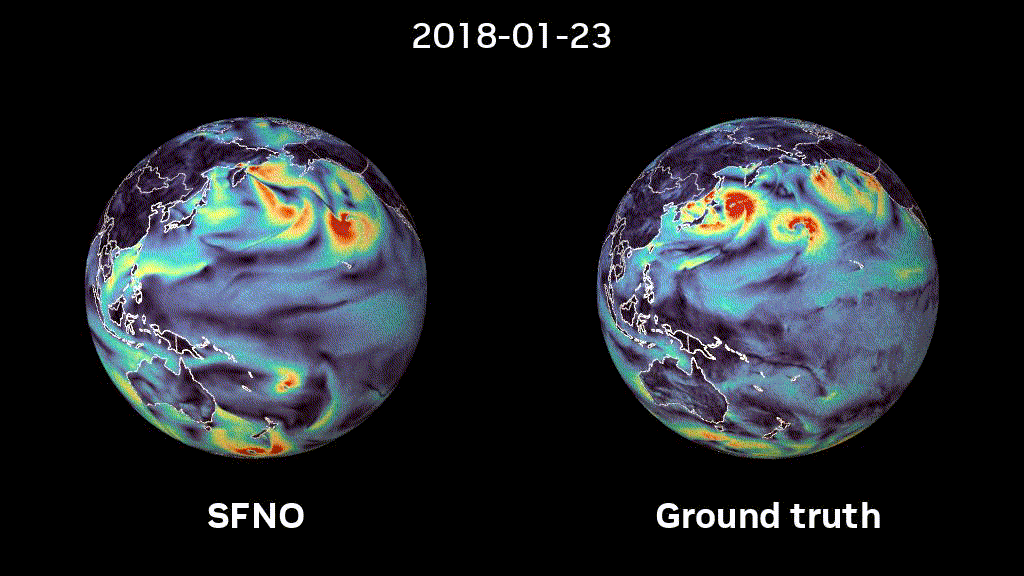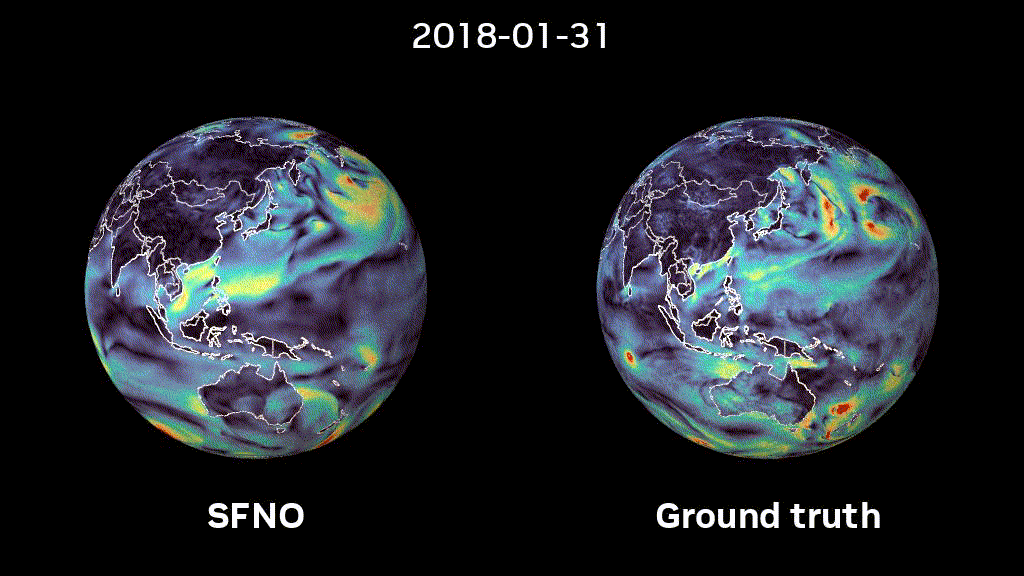
We trained SFNOs on the ERA5 dataset, provided by the European Centre for Medium-range Weather Forecasts (ECMWF). This dataset represents our best understanding of the state of Earth’s atmosphere over the past 44 years. Figure 2 shows that SFNO shows no signs of artifacts over the poles and rollouts remain remarkably stable, over thousands of autoregressive steps, for up to a year (Figure 1).

These results pave the way for the deployment of ML-based weather prediction methods. They offer a glimpse of how ML-based methods may hold the key to bridging the gap between weather forecasting and climate prediction, in the holy grail of sub-seasonal-to-seasonal forecasting.

A single rollout of SFNOs for a year, which involves 1460 autoregressive steps, is computed in 13 minutes on a single NVIDIA RTX A6000. That is over a thousand times faster than traditional numerical weather prediction methods.

Such substantially faster forecasting tools open the door to the computation of thousands of possible scenarios in the same time that it took to do a single one using traditional NWP, enabling higher confidence predictions of the risk of rare but high-impact extreme weather events.