Wei Tan, Research Staff Member at IBM T. J. Watson Research Center shares how IBM is using NVIDIA GPUs to accelerate recommender systems, which use ratings or user behavior to recommend new products, items or content to users. Recommender systems are important in applications such as recommending products on retail sites, recommending movies or music on streaming media services, and recommending news items or posts on social media and networking services. Wei Tan’s team developed cuMF, a highly optimized matrix factorization system using CUDA to accelerate recommendations used in applications like these and more.
Wei Tan, Research Staff Member at IBM T. J. Watson Research Center shares how IBM is using NVIDIA GPUs to accelerate recommender systems, which use ratings or user behavior to recommend new products, items or content to users. Recommender systems are important in applications such as recommending products on retail sites, recommending movies or music on streaming media services, and recommending news items or posts on social media and networking services. Wei Tan’s team developed cuMF, a highly optimized matrix factorization system using CUDA to accelerate recommendations used in applications like these and more.
Brad: Can you talk a bit about your current research?
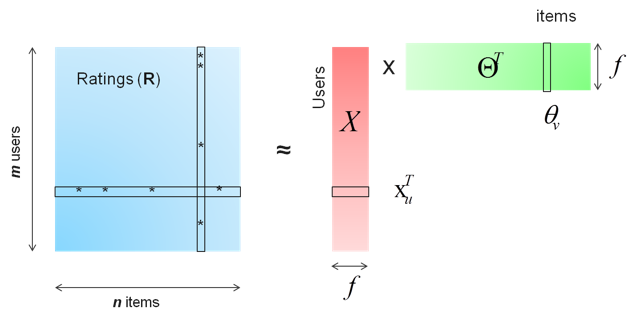
Wei: Matrix factorization (MF) is at the core of many popular algorithms, such as collaborative-filtering-based recommendation, word embedding, and topic modeling. Matrix factorization factors a sparse ratings matrix (m-by-n, with non-zero ratings) into a m-by-f matrix (X) and a f-by-n matrix (ΘT), as Figure 1 shows.
Suppose we obtained m users’ ratings on items (say, movies). If user u rated item v, we use as the non-zero element of R at position (u, v). We want to minimize the following cost function J. To avoid overfitting, we use weighted-λ-regularization proposed in [1], where
and
denote the number of total ratings on user u and item v, respectively.
Many optimization methods, including Alternating Least Squares (ALS) and Stochastic Gradient Descent (SGD) [1] have been applied to minimize . We adopt the ALS approach, which first optimizes X while fixing
, and then optimizes
while fixing X. That is, in one iteration we need to solve these two equations alternatively:
B: What are some of the biggest challenges in this project?
W: Recently, the GPU has emerged as an accelerator for parallel algorithms. It has massive computing power (typically 10x higher floating-point operations per second (FLOP/s) versus a CPU) and memory bandwidth (typically 5x versus a CPU), but with limited amount of control logic and memory capacity. Particularly, the GPU’s success in deep learning inspired us to try GPUs for MF. In deep learning, the computation is mainly dense matrix multiplication which is compute bound. As a result, a GPU can train deep neural networks 10x as fast as a CPU by saturating its FLOP/s. However, unlike deep learning, a MF problem involves sparse matrix manipulation which is usually memory bound. Given this, we want to explore a MF algorithm and a system that can still leverage the GPU’s compute and memory capability.
Given the widespread use of MF, a scalable and speedy implementation is very important. There are two challenges:
- On a single GPU, MF deals with sparse matrices, which makes it difficult to utilize the GPU’s compute power.
- We need to scale to multiple GPUs to deal with large, industry-scale problems (hundreds of millions of non-zero ratings).
B: What NVIDIA technologies are you using to overcome the challenges?
W: We developed cuMF, a CUDA-based matrix factorization library that optimizes the alternating least square (ALS) method to solve very large-scale MF. cuMF uses CUDA 7.0+, cuBLAS and cuSPARSE, and has been tested on both Kepler (Tesla K40/K80) and Maxwell (Titan X) GPUs.
cuMF achieves excellent scalability and performance by innovatively applying the following techniques on GPUs:
(1) On a single GPU, we optimize memory access in ALS by various techniques including reducing discontiguous memory access, retaining hotspot variables in faster memory, and aggressively using registers. These techniques allow cuMF to get closer to the roofline performance of a single GPU. See Figure 2.
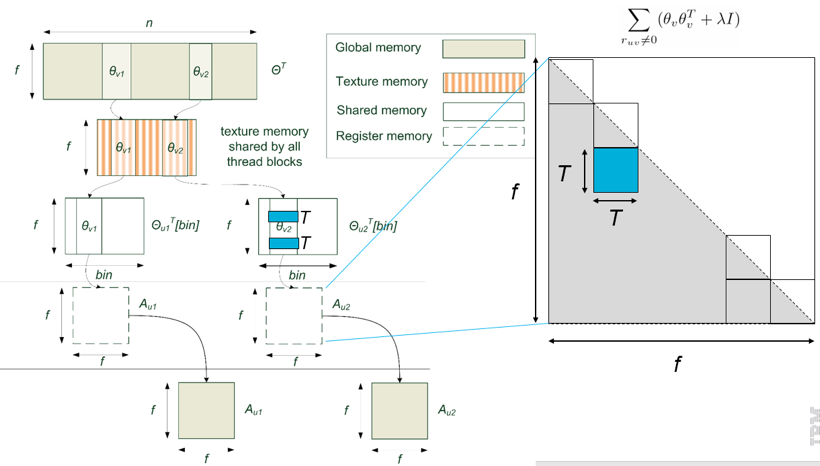
(2) On multiple GPUs, we add data parallelism to ALS’s inherent model parallelism. Data parallelism needs a faster reduction operation among GPUs, leading to (3).
In distributed machine learning, model parallelism and data parallelism are two common schemes. Model parallelism partitions parameters among multiple learners with each one learns a subset of parameters. Data parallelism partitions the training data among multiple learners so that each one learns all parameters from its partial observation. These two schemes can be combined when both the number of model parameters and the training data are large.
Model parallelism. As seen from equation 1, the solution of each is independent so model parallelism is straightforward.
Data parallelism. To tackle large-scale problems, on top of the existing model parallelism, we design a data-parallel approach. When is big and cannot stay in one GPU, we re-write the summation matrix in eq. 1 to its data-parallel form as:
That is, instead of transferring all s to one GPU to calculate the sum, it calculates a local sum on each GPU with only the local
s, and reduces (aggregates) many local
s later (See Figure 3).
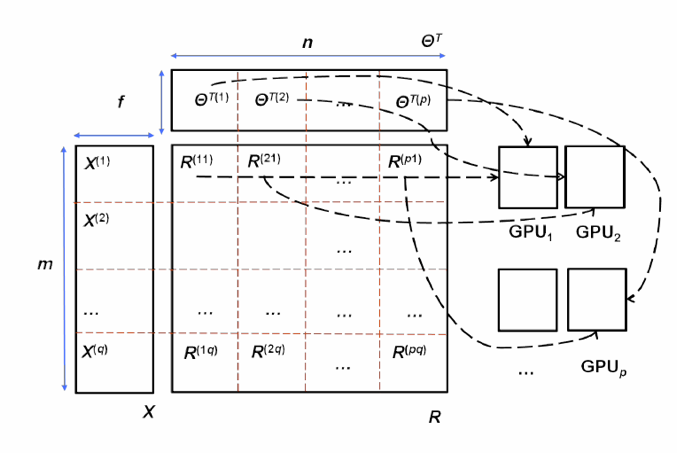
(3) We also developed an innovative topology-aware, parallel reduction method to fully leverage the bandwidth between GPUs. This way, cuMF ensures that multiple GPUs are efficiently utilized simultaneously.
The experimental results demonstrate that with up to four Titan X GPUs on one machine, cuMF is (1) competitive compared with multi-core methods, on medium-sized problems; (2) much faster than vanilla GPU implementations without memory optimization; (3) 6 to 10 times as fast, and 33 to 100 times as cost-efficient as distributed CPU systems, on large-scale problems; (4) more significantly, able to solve the largest matrix factorization problem ever reported.
![Table 1. Speed and cost of cuMF on one machine with four GPUs, compared with three different CPU systems in the cloud. Note: experiment details are in our paper [2].](https://developer.nvidia.com/blog/parallelforall/wp-content/uploads/2016/05/Table-1.png)
CuMF can be used standalone, or to accelerate the ALS implementation in Spark MLlib. We modified Spark’s ml/recommendation/als.scala (code) to detect GPUs and offload the ALS forming and solving to GPUs, while retain shuffling on Spark RDDs.
This approach has several advantages. First, existing Spark applications relying on mllib/ALS need no change. Second, we leverage the best of Spark (to scale-out to multiple nodes) and GPUs (to scale-up in one node).
B: What is the impact of your research to the larger data science community?
W: First, by using cuMF for matrix factorization, a large category of workloads that derive latent features from observations can be accelerated. These workloads include recommendation, topic modeling and word embedding.
Second, cuMF sheds light on accelerating machine learning algorithms involving sparse and graph data. We are glad to see that NVIDIA is also moving toward this direction by releasing nvGRAPH in the forthcoming CUDA 8.
B: When and why did you start looking at using NVIDIA GPUs?
W: We started looking at using NVIDIA GPUs to solve this problem in late 2014. We thought NVIDIA GPUs massive floating point throughput and large memory bandwidth would help in accelerating MF.
What is your GPU Computing experience and how have GPUs impacted your research?
It was a very smooth experience learning and using CUDA. I learned a lot from the two online parallel programming courses that both use CUDA — Intro to Parallel Programming and Heterogeneous Parallel Programming. There are a few excellent books that I can refer to, including Programming Massively Parallel Processors: A Hands-on Approach, by David Kirk and Wen-mei Hwu. In addition, I always get useful information and answers from the NVIDIA Forums.
GPUs have helped cuMF to be the state-of-the-art MF solution in terms of speed. Our research result is to be published in HPDC [2], a premier high performance computing conference.
B: What’s next for cuMF?
W: We have open-sourced cuMF. In future work we plan to make cuMF more user-friendly by providing a Python interface. We also want to further enhance it by using the latest hardware and software features such as NVLink, FP16 and NCCL.
B: In terms of technology advances, what are you looking forward to in the next five years?
W: In my personal opinion, in the next five years HPC technology is going to impact many aspects of machine learning. HPC has enabled and will keep enabling much more sophisticated machine learning, dealing with even bigger data, in data center and on devices.
Learn More!
You can read the HPDC paper describing cuMF linked in reference [2], below, or watch the GTC 2016 talk. If you’d like to try out cuMF, check out the source code on Github.
If you are interested in data analytics applications on GPU, you may be interested in the new nvGraph library.
References
[1] Y. Koren, R. M. Bell, and C. Volinsky, Matrix factorization techniques for recommender systems. Computer, vol. 42, no. 8, pp. 30- 37, 2009.
[2] Wei Tan, Liangliang Cao, Liana Fong. Faster and Cheaper: Parallelizing Large-Scale Matrix Factorization on GPUs. HPDC, Kyoto, Japan, 2016