在第一篇文章 时空蓝色噪声实时渲染,第 1 部分 中,我们将时间轴和重要性采样引入蓝色噪波纹理。在这篇文章中,我们将深入了解,展示一些扩展,并解释一些最佳实践。
有关更多信息,请在 GitHub 上的 NVIDIAGameWorks/SpatiotemporalBlueNoiseSDK 下载时空蓝色噪声纹理和生成代码。
蓝色噪音是如何工作的,为什么?
蓝色噪波纹理中的相邻像素彼此具有非常不同的值,包括环绕相邻像素,就像纹理是平铺的一样。假设您有一个渲染像素的函数,在 x 中的小变化导致 y 中的小变化, x 中的大变化导致 y 中的大变化。
当为 x 输入非常不同的邻居值时,也会为 y 输出非常不同的邻居值,从而使渲染结果具有蓝色噪波错误模式。除非像素渲染函数是散列函数,否则此假设通常适用于几何体边或着色不连续。
还值得注意的是,时空蓝色噪声中的每个像素都是随时间推移的渐进蓝色噪声序列,但从序列中的任何一点开始都是渐进的。这可以在查看 DFT 时看到,并记住傅里叶变换假设被变换序列的无限重复。
蓝色噪波中没有会扭曲频率内容的接缝。这意味着,当使用 TAA 时,每个像素在不同的时间线上抛出其历史记录,当拒绝历史记录时,每个像素立即处于良好的渐进采样序列上,而不是处于较差的序列上,直到序列重新启动,这在其他采样策略中很常见。这样,时空蓝色噪声中的每个像素都是环形渐进的。
值得一提的是,在 TAA 下运动的像素失去了时间上的好处,我们的噪声就如同纯粹的空间蓝色噪声。然而,在一瞬间仍然是偶数的像素获得了时间稳定性和较低的误差,当它们再次运动时,这将由 TAA 携带。在这些情况下,我们的噪声并不比空间蓝色噪声差,因此应始终使用它,以在可用的情况下获得好处,并在其他情况下不会更差。
蓝色噪声去噪
由于数字信号处理的原因,蓝色噪声比白色噪声更容易从图像中去除。白噪声在所有频率中具有随机化,而蓝噪声仅在高频中具有随机化。
模糊(如长方体滤波器或高斯模糊)是一种低通滤波器,这意味着它可以去除高频,但可以保持低频。
- 当白噪声模糊时,由于低通滤波器的低频随机化,它会变成噪声斑点。
- 当蓝色噪声模糊时,高频噪声消失,图像的低频部分保持不变。
蓝色噪声在其创建过程中使用高斯能量函数,因此经过优化,可以通过高斯模糊去除。如果您使用高斯函数模糊蓝色噪声,并且看到噪声斑点仍然存在,这意味着您必须在模糊中使用较大的 sigma ,因为蓝色噪声通过滤波器的频率较低。在去除这些斑点和在去噪图像中保留更多细节之间可能存在一种平衡。这取决于你的喜好。
图 2 、 3 和 4 显示了在使用原始噪声和去噪时,蓝色噪声与白色噪声的比较。
在图 3 中,两个图像总共只有八种颜色,因为它们每个颜色通道只有 1 位。蓝色噪声 – 抖动图像中有更多可识别和更精细的细节!
要了解为什么蓝色噪声比白色噪声去噪效果更好,请在频率空间中查看它们。通过卷积应用高斯模糊,这与频率空间中的逐像素乘法相同。
- 如果你用高斯核频率乘以蓝色噪声频率,就什么都不剩了,而且全是黑色的;高斯模糊消除蓝色噪声。
- 如果你用高斯核频率乘以白噪声频率,你会得到高斯核频率的形状(低频),但它们是随机的。这些是模糊白噪声后留下的斑点。
图 5 显示了蓝噪声、白噪声和高斯模糊核的频率大小。
平铺蓝色噪音
由于没有任何较大的比例(较低的频率)内容,蓝色噪声平铺良好。图 6 显示了这一点,但也显示了蓝色噪波平铺在较低分辨率下变得更加明显。这一点很重要,因为蓝色噪波纹理通常在屏幕上平铺,并在屏幕空间中使用。如果在使用蓝色噪波时注意到平铺,则应尝试使用分辨率更高的蓝色噪波纹理。
每像素获取多个值
有时,您可能希望每个像素具有多个时空蓝色噪波值,例如在渲染每个像素的多个采样时。
一种方法是以固定的偏移量读取纹理。例如,如果在(像素 x ,像素 y ) %textureSize 处读取第一个值,则可能在(像素 x + 5 ,像素 y + 7 ) %textureSize 处读取第二个值。这本质上为您提供了一个不相关的时空蓝色噪波值,就像您有第二个正在读取的时空蓝色噪波纹理一样。
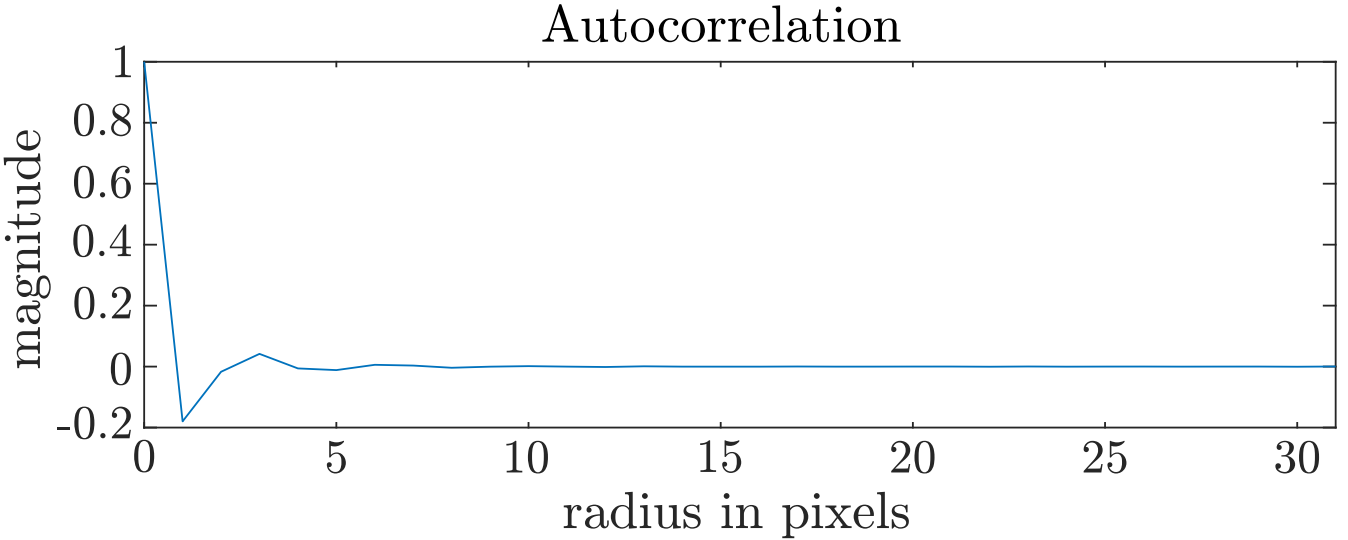
之所以这样做,是因为蓝色噪波纹理仅在短距离内具有相关性。在长距离情况下,这些值是不相关的,如图 7 所示。
理想情况下,如果您想要 N 时空蓝色噪波值,则应在彼此最大间隔的 N 偏移处读取蓝色噪波纹理。这样做的一个好方法是有一个渐进的低差异序列,在其中插入随机数索引,它会为您提供一个读取纹理的偏移量。
我们已经非常成功地使用 马丁·罗伯特的 R2 序列 插入索引,在[0 , 1]中获得 2D 向量,然后乘以蓝色噪波纹理大小以获得要读取的偏移量。
不过,还有另一种方法可以通过向每个像素添加秩 1 晶格来获得每个像素的多个值。这样做时,它类似于晶格上的 Cranley-Patterson 旋转,但使用蓝色噪声而不是白色噪声。
- 对于标量蓝色噪声,我们使用黄金比率或二的平方根得到了很好的结果。
- 对于非单位 vec2 蓝色噪声,我们使用 Martin Robert 的 R2 序列得到了很好的结果。
实际上,您可以使用相同的方法将 2D 蓝色噪波纹理转换为时空蓝色噪波,但在该过程中会丢失一些质量。有关更多信息,请参阅 SIGGRAPH 2021 年关于此方法的论文 使用蓝色噪声误差分布构建屏幕空间采样器时的经验教训和改进 。
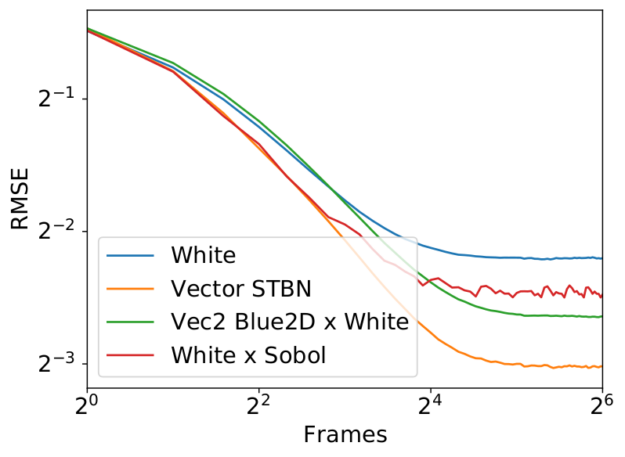
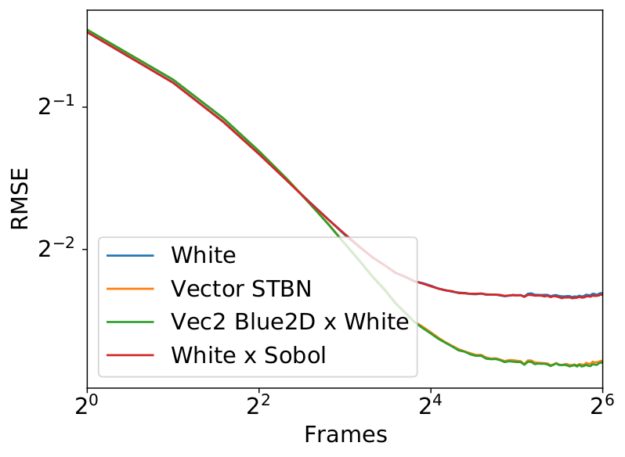
这种方法有时比时空蓝噪声收敛得更好,但误差图更不稳定,使其时间稳定性降低,并破坏蓝噪声频谱。图 8 显示了频率损伤,图 8 显示了一些收敛行为。有关收敛特性的更多信息,请参阅本文后面的简单函数收敛部分。
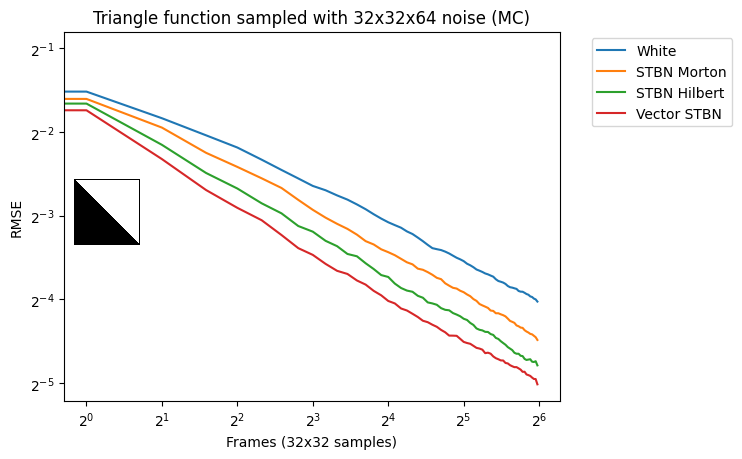
图 9 显示了将真实矢量时空蓝色噪声与 R2 低差异序列进行比较的图表, R2 低差异序列使用单个矢量蓝色噪声纹理进行 Cransley-Patterson 旋转。
这两种方法是其他方法之前设置蓝色噪波动画的方式。蓝色噪波纹理在每帧上偏移,这使其在空间上为蓝色噪波,在时间上为白色噪波,或者在低差异序列中播种蓝色噪波值,使其在空间上为损坏的蓝色噪波,但在时间上为良好的收敛序列。
通过曲线反演生成矢量值时空蓝噪声
如果你有一个标量时空蓝色噪声纹理,你可以把它通过一个倒置的莫顿或希尔伯特曲线,使它成为一个向量值时空蓝色噪声纹理。我们用希尔伯特曲线得到了更好的结果。虽然这些纹理的表现不如其他制造时空蓝色噪声的方法,但速度要快得多,甚至可以实时完成(图 10 )。
这种方法的一个有趣之处是,我们发现它可以很好地处理各种抖动掩模或其他标量值(灰度)噪声模式:拜耳矩阵 交错梯度噪声 ,甚至是样式化的噪声模式。
在所有这些情况下,当在渲染中使用向量时,会导致错误模式,这些错误模式采用源纹理的特性和外观。这对于样式化的噪波渲染可能很有趣,但也意味着将来,如果发现其他标量采样遮罩,则可以使用此方法将它们转换为具有相同属性的向量值遮罩。
分层
只有在下列条件成立时,向量值时空蓝色噪声的能量函数才能修改为返回非零:
- 像素来自相同的切片(相同的 z 值)
- 交换中涉及的像素的时间直方图不会变差
如果你这样做,你最终会得到在空间上呈蓝色,但随着时间分层的噪音;分层顺序是随机的。因为分层不是渐进的,所以在采集所有样本之前,它不会很好地收敛,但在这一点上效果很好(图 11 )。
高维蓝噪声
产生时空蓝色噪声的算法并不局限于 3D 。虽然到目前为止,我们还没有找到这些算法的使用案例,但这些算法可以进行简单的修改,以产生各种高维的蓝色噪声。如果时空蓝色噪声是 2Dx1D ,因为它在 XY 上是 2D 蓝色噪声,在 Z 上是 1D 蓝色噪声,图 12 显示了 4D 蓝色噪声的频率大小,分别是 2Dx2D 和 2Dx1Dx1D ,尺寸为 64x64x16x16 。
点集
使用 void 和 cluster 算法生成的蓝色噪波纹理可以阈值化为一个百分比值。许多像素在阈值化后存活下来,它们是蓝色噪声分布的。我们的标量值时空蓝噪声纹理具有相同的属性,并产生时空蓝噪声点集。图 13 显示了标量时空蓝色噪声纹理的阈值点,以及这些阈值点的频率振幅。
这些点集使得每一帧的像素都以令人愉悦的空间蓝色噪声的方式分布,但每一帧也会得到不同的点集。这意味着,与白噪波或其他动画蓝噪波方法相比,随着时间的推移,您可以获得更多独特的像素。图 14 显示了图像的五帧累积样本,使用重要性图作为每像素蓝色噪声阈值。我们的噪波以最快的速度对最独特的像素进行采样,同时在空间上也提供了一个漂亮的蓝色噪波图案。
单函数收敛
在本节中,我们将讨论使用常见噪声类型的简单函数在蒙特卡罗积分和指数移动平均下的收敛性,以模拟 TAA 。
标量蒙特卡罗积分
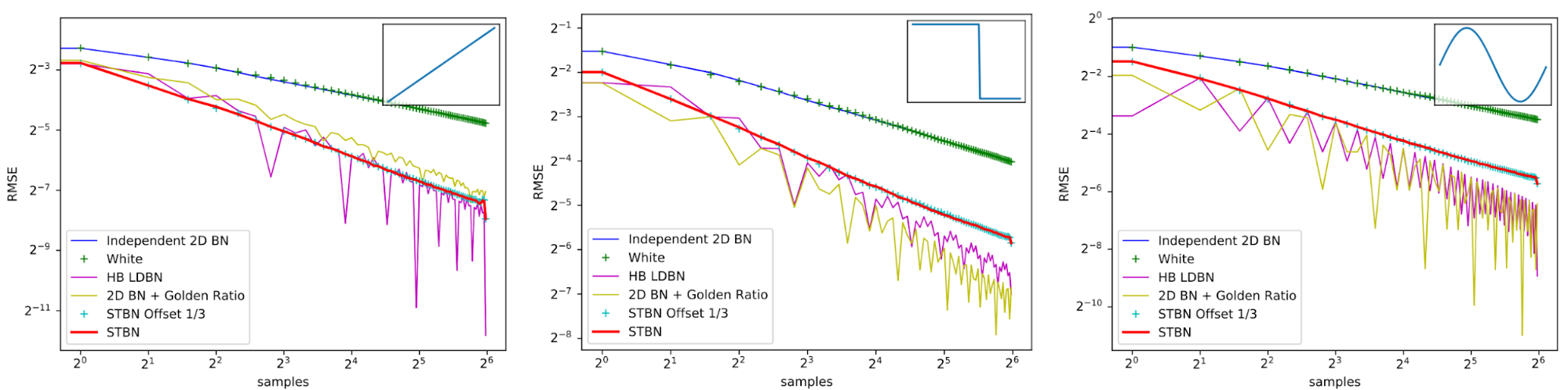
图 15 显示了 Monte Carlo 积分下的收敛速度,就像您在每像素采集多个样本时所做的一样。 HB LDBN 来自 一种低偏差取样器,将蒙特卡罗误差作为蓝色噪声分布在屏幕空间中 。虽然低差异序列可以比 STBN 做得更好,但它在时间上更稳定,并且由于在空间上是蓝色噪声而产生良好的感知误差。 STBN 偏移量 1 / 3 表明,如果从序列中的任意位置启动 STBN ,它仍然保持良好的收敛特性。这表明 STBN 是环向渐进的。
标量指数移动平均
图 16 显示了指数移动平均下的收敛速度。指数移动平均值以 0.1 的值从上一个值线性插值到下一个值。这模拟了无重投影或邻域采样拒绝的 TAA 。

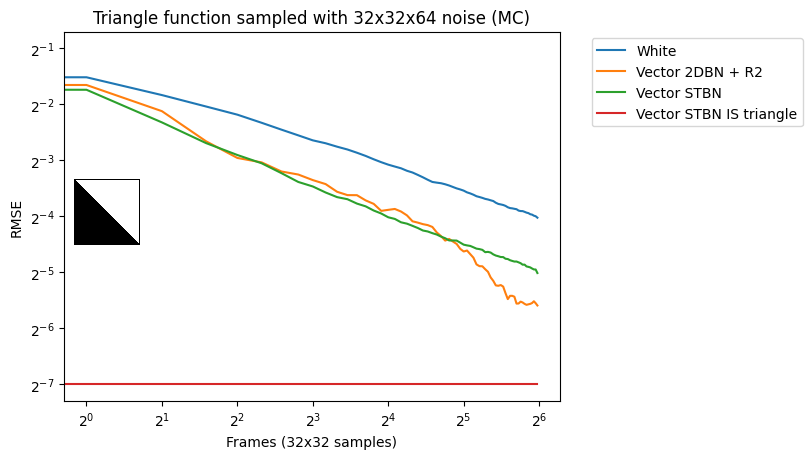
Vec2 蒙特卡罗积分
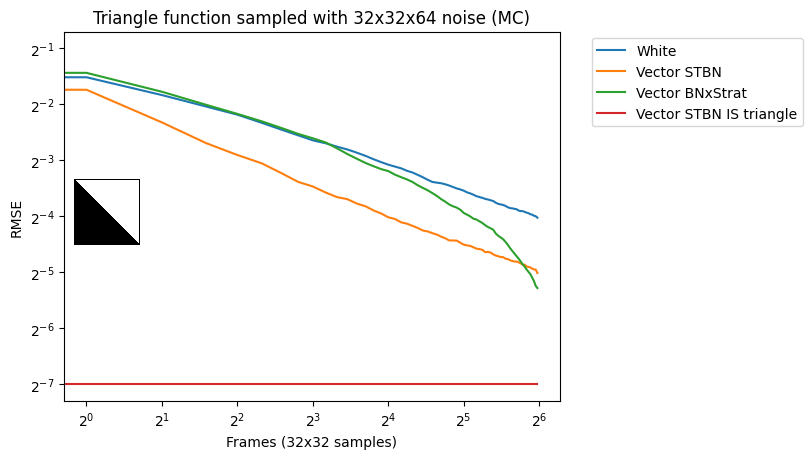
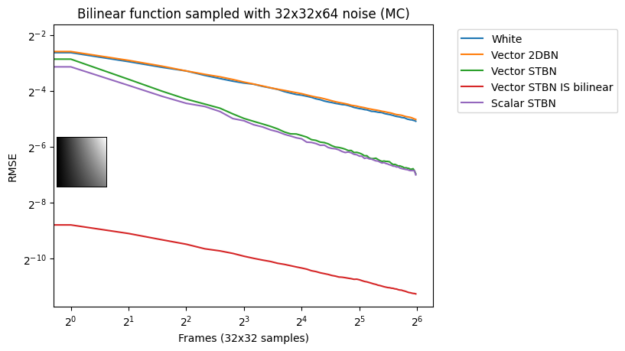
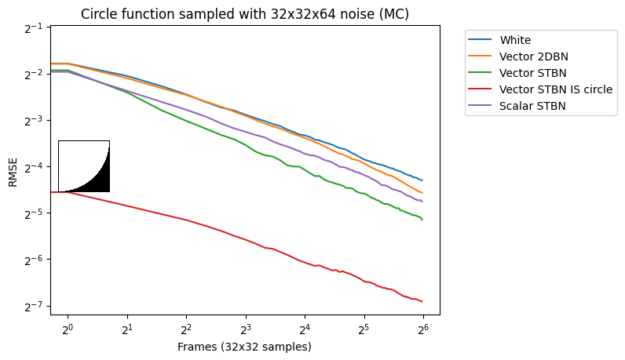
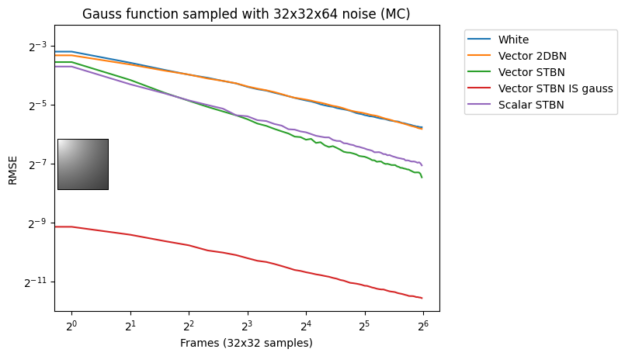
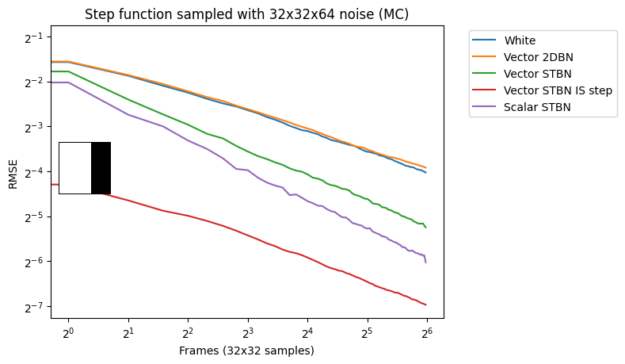
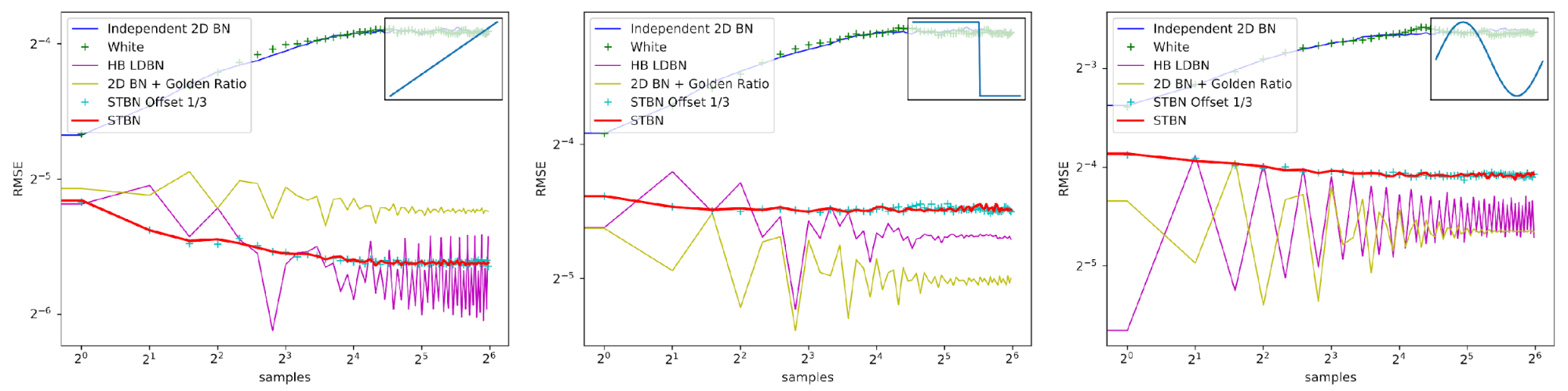
图 17 显示了蒙特卡罗积分下的收敛速度。标量 STBN 使用 R2 纹理偏移方法读取此 2D 积分的两个标量值。因此,它在阶跃函数(最终是一个一维问题)和双线性函数(最终是一个轴对齐问题)中的性能优于向量 STBN 。重要抽样有任何错误的原因都是由于向量和 PDF 值的离散化。
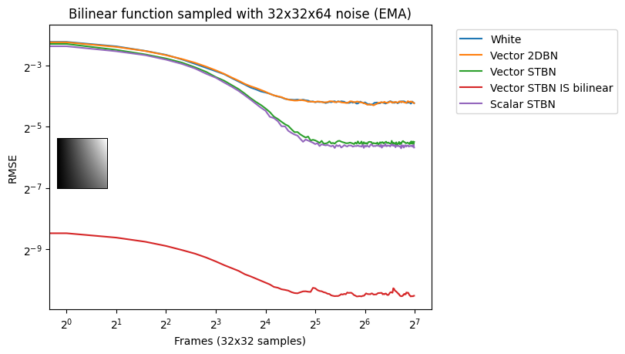
指数移动平均数
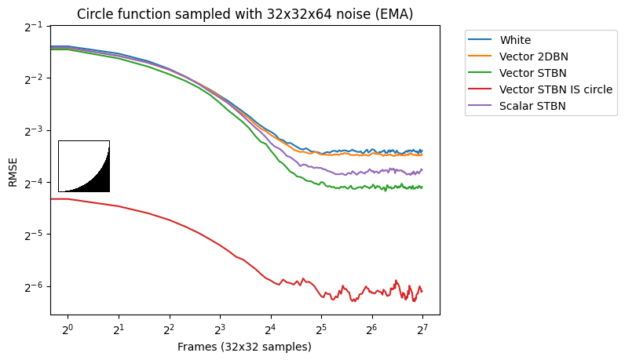
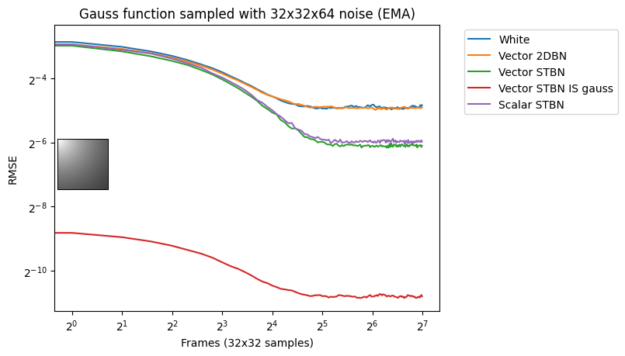
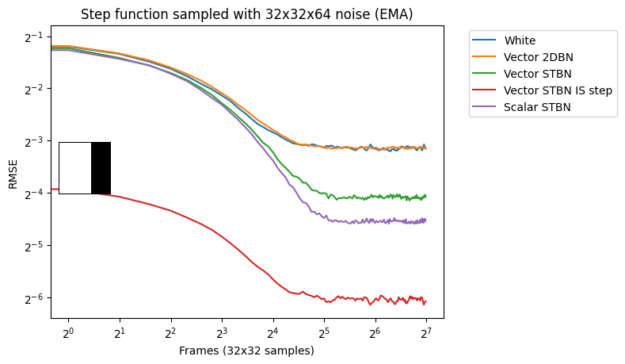
图 18 显示了 EMA 下的收敛。指数移动平均值以 0.1 的值从上一个值线性插值到下一个值。这模拟了无重投影或邻域采样拒绝的 TAA 。
结论
虽然蓝色噪声采样点近年来取得了进步,但几十年来,蓝色噪声纹理似乎在很大程度上被忽略了。如图所示,时空蓝色噪声纹理对于实时渲染具有几个理想的特性,在实时渲染中只能提供较低的采样数:良好的空间误差模式、更好的时间稳定性和收敛性,以及环形渐进性,仅举几例。
我们认为,这些纹理只是开始,因为还有其他几种改进采样纹理的可能性,无论它们是基于蓝色噪波的、混合的还是完全其他的。
但值得注意的是,还有其他方法可以在样本数最低的情况下获得很好的结果。例如, NVIDIA RTXDI 也适用于这种情况,但使用不同的方法。