设计深度网络以处理其他深度网络

深度神经网络（DNN）是从数据中学习函数的首选模型，如图像分类器或语言模型。近年来，深度模型由于表示数据样本本身而变得流行起来。例如，可以训练深度模型来表示图像、3D 对象或场景，这种方法称为Implicit Neural Representations（另请参阅 Neural Radiance Fields和Instant NGP)。请继续阅读一些对预训练的深度模型执行操作的示例，这些模型包括作为函数的 DNN 和作为数据的 DNN。

假设您有一个使用隐式神经表示（INR）或神经辐射场（NeRF）表示的 3D 对象数据集。通常，您可能希望“编辑”对象以更改其几何图形或修复错误和异常。‌例如，拆除一个杯子的把手或使所有车轮比 NeRF 重建的车轮更对称。

不幸的是，使用 INR 和 NeRF 的一个主要挑战是，它们必须在编辑之前进行渲染。实际上，编辑工具依赖于渲染对象并直接微调 INR 或 NeRF 参数。例如，3D 神经雕塑 (3DNS)：编辑神经符号距离函数直接改变 NeRF 模型的权重而不将其渲染回 3D 空间会更有效。

作为第二个例子，考虑一个经过训练的图像分类器。在某些情况下，您可能希望将某些转换应用于分类器。例如，您可能希望使用在下雪天气中训练的分类器，使其对阳光充足的图像准确无误。这是一个领域自适应问题的例子。

然而，与传统的域自适应方法不同，该设置侧重于学习将函数（分类器）从一个域映射到另一个域的一般操作，而不是将特定分类器从源域转移到目标域。

处理其他神经网络的神经网络

我们团队提出的关键问题是神经网络能否学会执行这些操作。我们寻求一种特殊类型的神经网络“处理器”，可以处理其他神经网络的权重。

这反过来又提出了一个重要的问题，即如何设计能够处理其他神经网络权重的神经网络。这个问题的答案并没有那么简单。

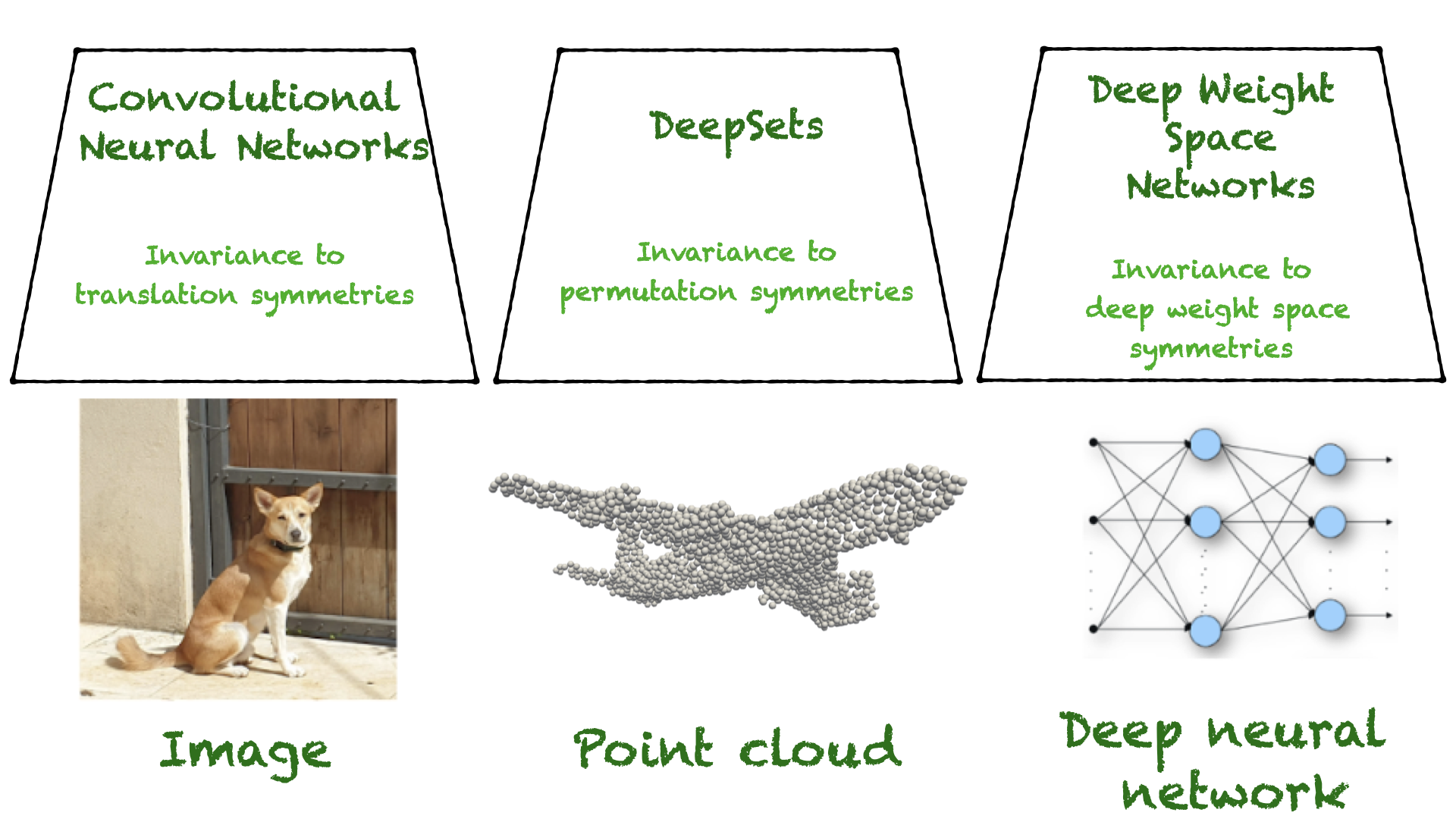
This figure illustrates three deep networks, for three spaces that have invariance properties: Images are invariant to translation, point clouds are invariant to permutations, and neural networks are invariant to deep-weight-space symmetries. Each data type has data-specialized architectures: convolutional neural networks for images and DeepSets for point clouds, and deep-weight-space networks for the third case. — *图 1。数据专用架构的两个示例：用于图像的卷积神经网络和用于点云的 DeepSets*

以前处理深权重空间的工作

表示深度网络参数的最简单方法是将所有权重（和偏差）矢量化为简单的平面向量。‌然后，应用一个全连接网络，也称为多层感知器（MLP）。

一些研究已经尝试了这种方法，并表明这种方法可以预测输入神经网络的测试性能。详情请参见Classifying the Classifier: Dissecting the Weight Space of Neural Networks， Hyper-Representations: Self-Supervised Representation Learning on Neural Network Weights for Model Characteristic Prediction和 Predicting Neural Network Accuracy from Weights。

不幸的是，这种方法有一个主要缺点，因为神经网络权重的空间具有复杂的结构（下面将更全面地解释）。将 MLP 应用于所有参数的矢量化版本会忽略该结构，因此会损害泛化能力。这种效果类似于其他类型的结构化输入，如图像。这种情况最适用于对输入图像的小偏移不敏感的深度网络。

解决方案是使用卷积神经网络。它们的设计方式在很大程度上对图像的变化“视而不见”，因此，可以推广到训练中没有观察到的新变化。

在这里，我们希望设计遵循相同想法的深层架构，但我们希望设计对模型权重的其他转换不敏感的架构，而不是考虑图像偏移，如下所述。

具体来说，神经网络的一个关键结构特性是，它们的权重可以被排列，同时它们仍然计算相同的函数。图 2 说明了这种现象。当将全连通网络应用于矢量化权重时，忽略了这一重要特性。

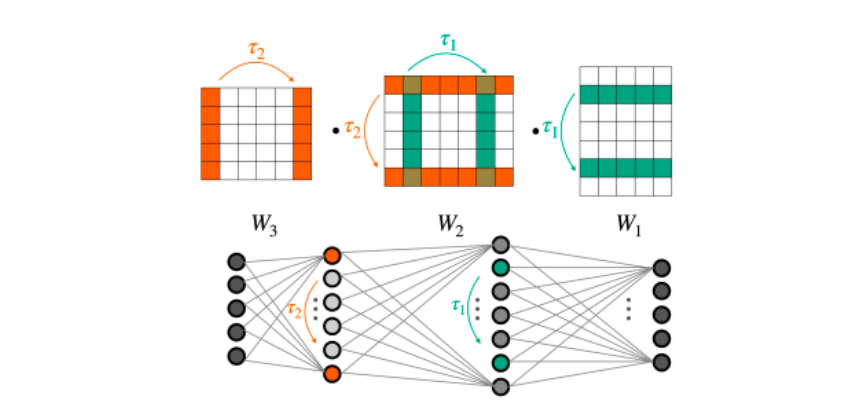
The figure illustrates the weight symmetries of a multilayer perceptron (MLP) with two hidden layers. Changing the order of neurons in internal layers preserves the function represented by the MLP. — *图 2:具有两个隐藏层（底部）的多层感知器（MLP）的权重对称性（顶部）。改变内层神经元的顺序可以保留 MLP 所代表的功能*

不幸的是，一个在平面向量上运行的全连接网络认为所有这些等价表示都是不同的。这使得网络更难在所有此类（等效）表示中进行泛化。

对称性和等变体系结构简介

幸运的是，前面的 MLP 限制已经在机器学习的一个子领域进行了广泛的研究，即几何深度学习（GDL）。GDL 是关于学习对象，同时对这些对象的一组变换保持不变，比如移动图像或排列集。这组转换通常被称为对称群。

在许多情况下，‌学习任务对这些转换是不变的。例如，查找点云的类应该与点在网络中的顺序无关，因为该顺序无关紧要。

在其他情况下，如点云分割，云中的每个点都被分配了一个类，它属于对象的哪个部分。在这些情况下，如果输入被排列，输出点的顺序必须以相同的方式改变。这些函数的输出根据输入变换进行变换，称为等变的功能。

更正式地说，对于一组变换 G，函数 L:V→ 如果 W 与群作用交换，则称为 G-等变，即对于所有 v∈v，G∈G，L（gv）=gL（v）不变的作用

在不变函数和等变函数这两种情况下，限制假设类都是非常有效的，并且这种对称感知架构由于其有意义的归纳偏差而提供了几个优点。例如，它们通常具有更好的样本复杂性和更少的参数。在实践中，这些因素导致了明显更好的概括。

权重空间的对称性

本节解释深权重空间的对称性。有人可能会问这样一个问题：哪些转换可以应用于 MLP 的权重，这样 MLP 表示的底层函数就不会改变？

一种特定类型的转换，称为神经元排列，是这里的焦点。直观地说，当观察 MLP 的图形表示时（如图 2 中的图），改变某个中间层神经元的顺序不会改变函数。此外，可以针对每个内部层独立地进行重新排序过程。

在更正式的术语中，MLP 可以使用以下方程组来表示：

$f(x)= x_M, \quad x_{m+1}=\sigma(W_{m+1} x_m +b_{m+1}), \quad x_0=x$

这个重量空间该体系结构的定义为（线性）空间，包含所有矢量化权重和偏差的串联 $[W_m, b_l]_{ m \in [M],l\in[M]}$ 重要的是，在该设置中，权重空间是（即将定义的）神经网络的输入空间。

那么，权重空间的对称性是什么？对神经元进行重新排序可以被形式化建模为将排列矩阵应用于一层的输出，并将相同的排列矩阵应用到下一层。形式上，一组新的参数可以由以下方程定义：

$W_1 \rightarrow P^T W_1$

$W_2 \rightarrow W_2P$

新的参数集是不同的，但很容易看出，这样的转换不会改变 MLP 表示的函数。这是因为两个置换矩阵 $P$ 和 $P^T$ 相互抵消（假设像 ReLU 这样的元素激活函数）。

更一般地，如前所述，不同的排列可以独立地应用于 MLP 的每一层。这意味着更多一般的转换集不会改变底层函数。把这些想象成对称性重量空间。

$(W_1,\dots,W_M) \rightarrow (P_1^TW_1,P_2^TW_2P_1,\dots,P_{M-1}^TW_{M-1}P_{M-2},W_MP_{M-1})$

在这里 $P_i$ 表示置换矩阵。30 多年前，赫奇特·尼尔森在《前馈网络权重空间的代数结构》中提到，类似的变换可以应用于 MLP 的偏差。

构建深度权重空间网络

文献中的大多数等变体系结构都遵循相同的配方：定义了一个简单的等变层，体系结构被定义为这些简单层的组成，它们之间可能存在点非线性。

一个很好的例子是 CNN 架构。在这种情况下，简单的等变层执行卷积运算，而 CNN 则被定义为多个卷积的组合。DeepSets 和许多 GNN 架构都遵循类似的方法。想要了解更多信息，请参阅 Weisfeiler 和 Leman 的神经网络：高阶图神经网络和不变和等变图网络。

当手头的任务是不变的时，可以使用 MLP 在等变层的顶部添加一个不变层，如图 3 所示。

The figure illustrates a typical equivariant architecture. It is composed of several simple equivariant layers, followed by an invariant layer and finally a fully connected layer. — *图 3。一种典型的等变体系结构，由几个简单的等变层组成，然后是一个不变层和一个完全连接层*

我们在论文 Equivariant Architectures for Learning in Deep Weight Spaces 中遵循这个配方，我们的主要目标是为上面定义的权重空间对称性识别简单但有效的等变层。不幸的是，刻画一般等变函数的空间可能具有挑战性。与之前的一些研究一样（例如 Deep Models of Interactions Across Sets），我们的目标是刻画所有线性的等变层。

我们开发了一种新的方法来表征线性等变层，该方法基于以下观察结果：权重空间 V 是表示每个权重矩阵 V=ŞWi 的更简单空间的级联。（为简洁起见，省略了偏差术语）。

这一观察结果很重要，因为它可以写入任何线性层 $L:V \rightarrow V$ 作为块矩阵，其第（i，j）个块是介于 $W_j$ 和 $W_i$ $L_{ij} : W_j \rightarrow W_i$ .该块结构如图 4 所示。

但我们如何才能找到 $L_{ij}$ ? 我们的论文列出了所有可能的情况，并表明其中一些层已经在以前的工作中得到了表征。例如， $L_{ii}$ 对于内层，其特征在于 Deep Models of Interactions Across Sets。

值得注意的是，在这种情况下，最一般的等变线性层是对只使用四个参数的众所周知的深集层的推广。对于其他层，我们提出了基于简单等变操作的参数化，如池化、广播和小的全连接层，并表明它们可以表示所有线性等变层。

图 4 显示了 L 的结构，它是特定权重空间之间的块矩阵。每种颜色代表不同类型的图层。 $L_{ii}$ 每个块将一个特定的权重矩阵映射到另一个权重矩阵。这种映射是以一种依赖于权重矩阵在网络中的位置的方式参数化的。

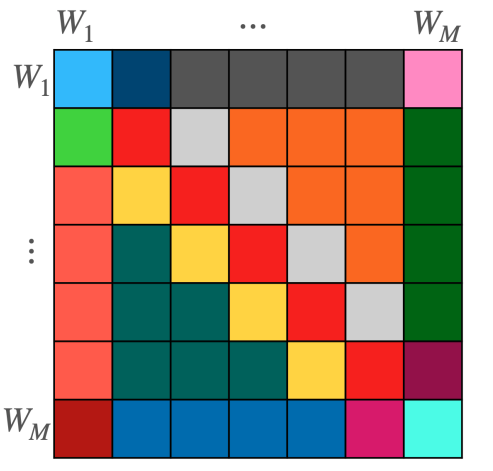
The figure shows colored squares within a larger square, illustrating the block structure of the proposed linear equivariant layer. Each block maps a specific weight matrix to another weight matrix. This mapping is parameterized in a way that relies on the positions of the weight matrices in the network. — *图 4。所提出的线性等变层的块结构*

该层是通过独立计算每个块，然后对每行的结果求和来实现的。我们的论文涵盖了一些额外的技术细节，比如处理偏差项和支持多个输入和输出特性。

我们将这些层称为深重空间层（DWS 层），并将由它们构建的网络称为深重量空间网络（DWSNets）。我们在这里关注的是将 MLP 作为输入的 DWSNets。有关 CNNs 和变压器扩展的更多详细信息，请参阅附录 H 中的Equivariant Architectures for Learning in Deep Weight Spaces。

深权空间网络的表现力

将我们的假设类限制为简单的等变函数的组合可能会无意中削弱等变网络的表达能力。这已经在上面引用的图神经网络文献中得到了广泛的研究。我们的论文表明 DWSNets 可以近似输入网络上的前馈操作，这是理解其表达能力的一步。然后，我们证明 DWS 网络可以近似 MLP 函数空间中定义的某些“性能良好”的函数。

实验

DWSNets 在两个任务族中进行评估。首先，采用表示数据的输入网络，如 INR。其次，采用表示标准 I/O 映射（如图像分类）的输入网络。

实验 1:INR 分类

此设置根据 INR 所代表的图像对其进行分类。具体来说，它涉及训练 INR 来代表 MNIST 和时尚 MNIST 的图像。任务是让 DWSNet 识别图像内容，如 MNIST 中的数字，使用这些 INR 的权重作为输入。结果表明，我们的 DWSNet 体系结构大大优于其他基线。

方法	MNIST INR	Fashion-MNIST INR
MLP	17.55%+-0.01	19.91%+-0.47
MLP+置换扩充	29.26%+-0.18	22.76%+-0.13
MLP+对齐	58.98%+-0.52	47.79%±1.03
INR2Vec（架构）	23.69%+-0.10	22.33%+-0.41
transformer	26.57%+-0.18	26.97%+-0.33
DWSNets（我们的）	85.71%+-0.57	67.06%+-0.29

表 1。对于 INR 分类，INR 的类别由其所代表的图像定义（平均测试精度)

重要的是，将 INR 分类到它们所代表的图像类别明显比对底层图像进行分类更具挑战性。在 MNIST 图像上训练的 MLP 可以实现近乎完美的测试精度。然而，接受 MNIST INRs 训练的 MLP 效果不佳。

实验 2：INRs 的自我监督学习

这里的目标是将神经网络（特别是 INRs）嵌入到语义连贯的低维空间中。这是一项重要的任务，因为良好的低维表示对许多下游任务至关重要。

我们的数据由拟合到形式为 a\sin（bx）的正弦波的 INR 组成，其中 a、b 是从区间 0,10 上的均匀分布中采样的。由于数据由这两个参数控制，因此密集表示应该提取这个底层结构。

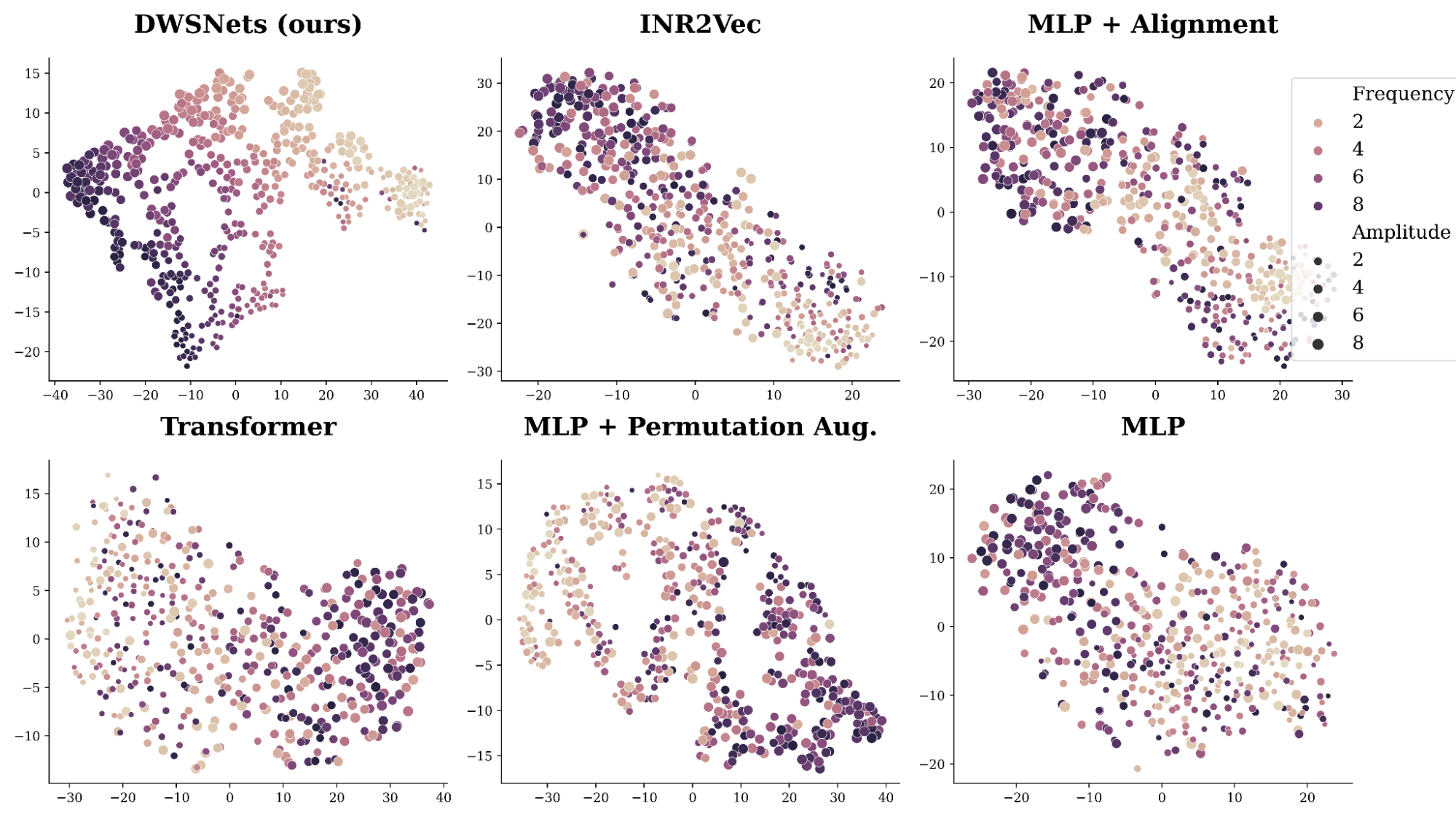
The figure shows 2D TSNE embeddings of input MLPs obtained by training using self-supervision. Each point corresponds to an input MLP that represents a 1D sine wave g(x)=a\sin(bx) with a different amplitude a and frequency b. DWSnets successfully reconstruct the amplitude-frequency space while other methods struggle. — *图 5。通过使用自我监督的训练获得的输入 MLP 的 TSNE 嵌入*

A.SimCLR 类似的训练过程和目标被用于通过添加高斯噪声和随机掩蔽来从每个 INR 生成随机视图。图 4 显示了结果空间的 2D TSNE 图。我们的方法 DWSNet 很好地捕捉到了数据的基本特征，而竞争方法却举步维艰。

实验 3：使预训练的网络适应新的领域

该实验展示了如何在不进行再训练的情况下使预训练的 MLP 适应新的数据分布（零样本域适应）。给定图像分类器的输入权重，任务是将其权重转换为一组新的权重，该权重在新的图像分布（目标域）上表现良好。

在测试时，DWSnet 接收一个分类器，并在一次前向传递中将其调整为新域。CIFAR10 数据集是源域，其损坏版本是目标域（图 6）。

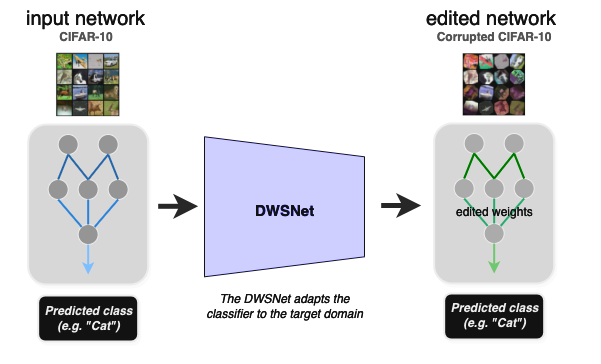
Domain adaptation using DWSNets. The DWSNet takes as input a network trained on a source domain (CIFAR10) and its taks is to change the weights such that the output network performs well on a target domain (a corrupted version of CIFAR10). — *图 6。使用 DWSNets 的域自适应*

结果如表 2 所示。注意，在测试时，模型应该推广到看不见的图像分类器，以及看不到的图像。

方法	CIFAR10->CIFAR10 已损坏
无适应	60.92%+-0.41
MLP	64.33%+-0.36
MLP+置换扩充	64.69%+-0.56
MLP+对齐	67.66%+-0.90
INR2Vec（架构）	65.69%+-0.41
transformer	61.37%+-0.13
DWSNets（我们的）	71.36%+-0.38

表 2。使网络适应新域。CIFAR-10 腐蚀模型的测试精度

未来研究方向

将学习技术应用于深度权重空间的能力开启了许多新的研究方向。首先，找到有效的数据扩充方案以在权重空间上提高 DWSNets 的泛化能力是可能的。其次，研究如何为其他类型的输入架构和层（如跳过连接或规范化层）合并排列对称性是很自然的。最后，将 DWSNets 扩展到真实世界的应用程序中会很有用，如形状变形和变形、NeRF 编辑和模型修剪。阅读 ICML 2023 论文全文，Equivariant Architectures for Learning in Deep Weight Spaces。

有几篇与此工作密切相关的论文，我们鼓励感兴趣的读者查阅。首先，论文 Permutation Equivariant Neural Functionals 提供了与此处讨论的问题类似的公式，但从不同的角度进行了探讨。其次，后续研究 Neural Functional Transformers 建议在线性等变层中使用注意力机制，而非简单的求和/平均聚合。最后，论文 Neural Networks Are Graphs! Graph Neural Networks for Equivariant Processing of Neural Networks 提出将输入神经网络建模为加权图，并应用 GNN 来处理权重空间。