由于时间序列数据固有的复杂性和不可预测性,对其建模可能具有挑战性(也很有吸引力)。例如,时间序列中的长期趋势可能会因某些事件而发生剧烈变化。回想一下全球疫情开始时,航空公司或实体店等企业的客户数量和销售额迅速下降。相比之下,电子商务业务继续运营,中断较少。
交互项可以帮助建模这种模式。它们能捕捉变量之间的复杂关系,从而产生更准确的预测。
这篇文章探讨:
- 时间序列预测中的交互项
- 建模复杂关系时交互术语的好处
- 如何在模型中有效地实现交互术语
交互术语概述
交互术语可以帮助您探究目标和功能之间的关系是否会随着另一个功能的值的变化而变化。想要了解更多详细信息,请参阅我之前的文章,线性回归中交互术语的全面指南。
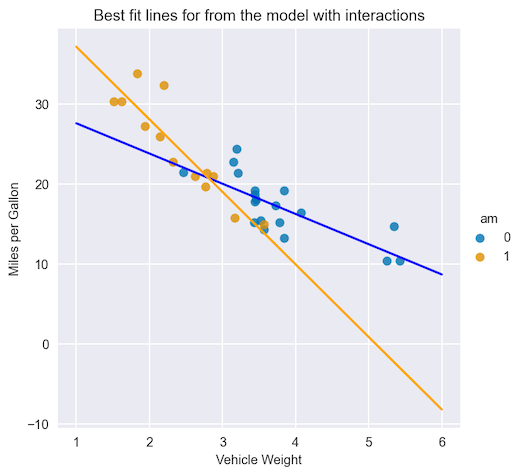
图 1 显示了一个散点图,表示每加仑英里数(目标)和车辆重量(特征)之间的关系。根据变速器类型(另一个特征)的不同,这种关系会大不相同。
提高线性模型精度
如果不使用交互项,线性模型将无法捕捉到如此复杂的关系。实际上,无论传输类型如何,它都会为权重特征分配相同的系数。图 1 显示了按权重特征划分的系数(线的斜率),不同传输类型的系数有很大不同。
为了克服这种谬论并使线性模型更加灵活,可以添加交互项。一般来说,它们是原始特征的乘积。通过将这些新变量添加到回归模型中,可以测量它们与目标之间相互作用的效果。
时间序列预测中的交互项
交互项使线性模型更加灵活。以下示例显示了它们在时间序列预测中的工作方式。
先决条件
首先,加载所需的库:
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
import seaborn as sns
import matplotlib.pyplot as plt
数据集生成
然后,生成一些具有以下特征的人工时间序列数据:
- 10 年的日常数据
- 时间序列中存在的重复模式(季节性)
- 前 7 年呈下降趋势
- 过去 3 年无趋势
- 随机噪声,作为最后一步添加
# for reproducibility
np.random.seed(42)
# generate the DataFrame with dates
range_of_dates = pd.date_range(
start="2010-01-01",
end="2019-12-30"
)
df = pd.DataFrame(index=range_of_dates)
# create a sequence of day numbers
df["linear_trend"] = range(len(df))
df["trend"] = 0.004 * df["linear_trend"].values[::-1]
df.loc["2017-01-01":, "trend"] = 4
# generate the components of the target
signal_1 = 10 + 4 * np.sin(df["linear_trend"] / 365 * 2 * np.pi)
noise = np.random.normal(0, 0.85, len(df))
# combine them to get the target series
df["target"] = signal_1 + noise + df["trend"]
# plot
df["target"].plot(title="Generated time series");
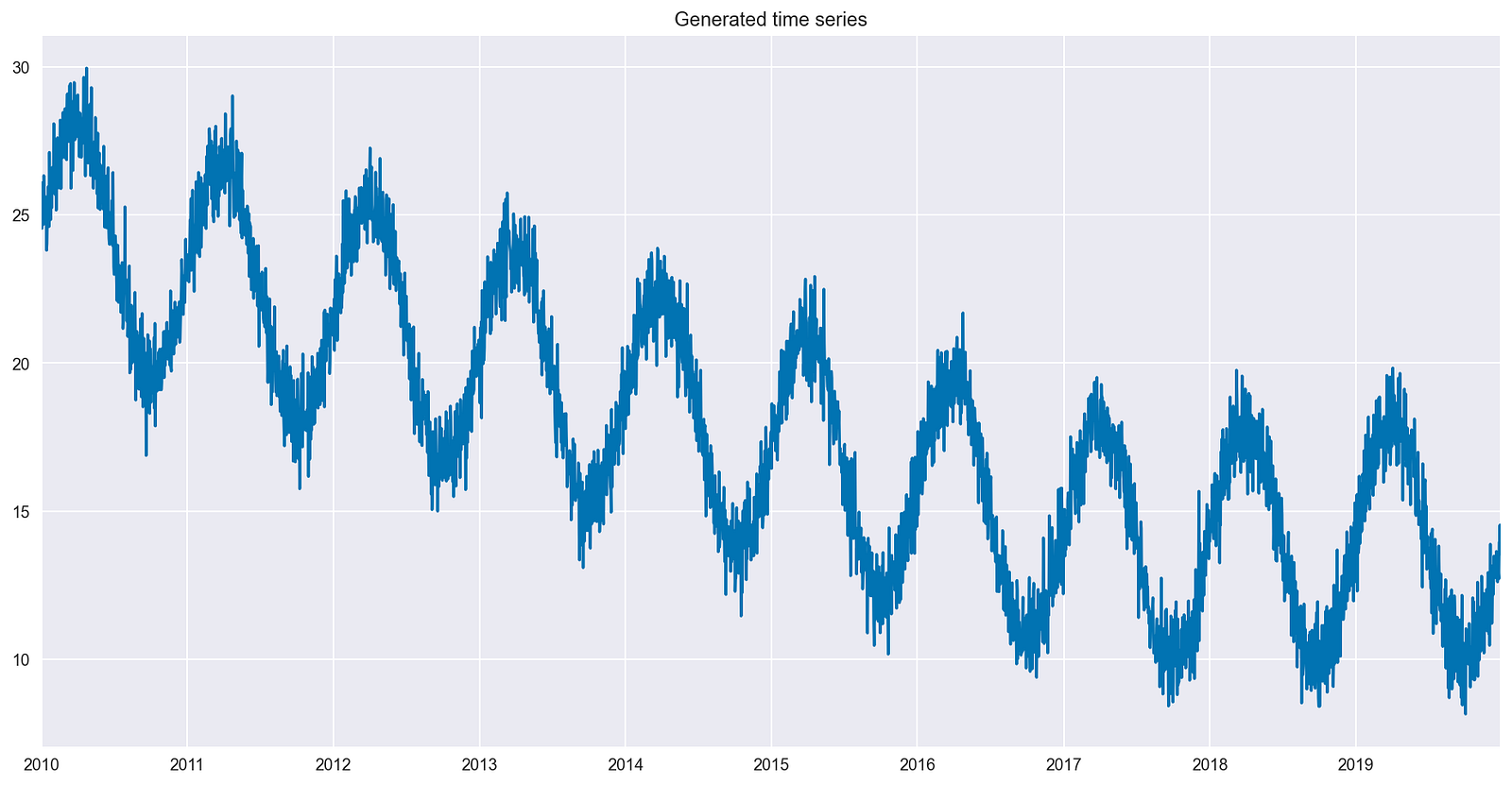
图 2 显示了生成的时间序列,其中包括所有所需的特性。
培训基准模
现在训练一个线性模型并检查最佳拟合线。对于这一步,创建具有一些功能的非常简单的模型。这使您能够直观地检查交互项对模型拟合的影响。
最简单的模型可能包含一个特性 — 时间流逝的指示器。这个linear_trend为时间序列创建的列实际上是 DataFrame 的行号(按日期排序)。
X = df[["linear_trend"]]
y = df[["target"]]
lm = LinearRegression()
lm.fit(X, y)
df["model_1"] = lm.predict(X)
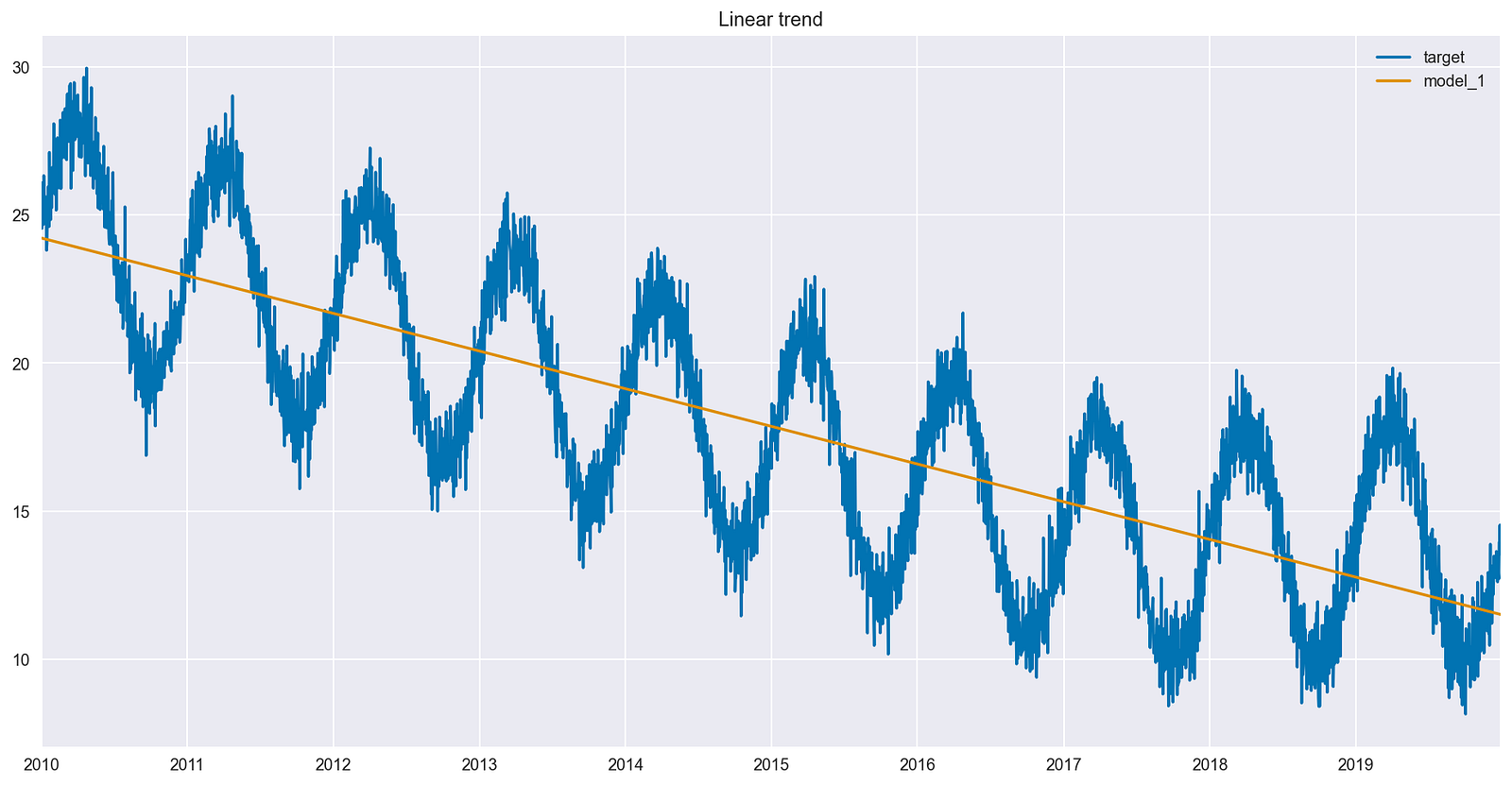
df[["target", "model_1"]].plot(title="Linear trend");
值得一提的是,重点不是使用单独的训练集和测试集来正确评估预测,而是解释交互项对模型拟合的影响。通过检查拟合值(对训练集的预测)并将这些拟合值与原始时间序列进行比较,更容易观察交互项的影响。
图 3 显示,线性模型确定了整个时间序列的下降趋势。与此同时,过去 3 年的数据似乎不符合,因为没有趋势。
添加断点
接下来,尝试使用特征工程使模型学习新模式(趋势变化)。为此,请创建一个断点,它是一个占位符变量,指示给定的观测值是否在 2017 年 1 月 1 日之后。在这种情况下,趋势变化发生的确切时间点是已知的。
接下来,训练另一个线性模型,这次有两个功能:
df["after_2017_breakpoint"] = np.where(df.index >= pd.Timestamp('2017-01-01'), 1, 0)
X = df[["linear_trend", "after_2017_breakpoint"]]
y = df[["target"]]
lm = LinearRegression()
lm.fit(X, y)
df["model_2"] = lm.predict(X)
df[["target", "model_2"]].plot(title="Linear trend + breakpoint");
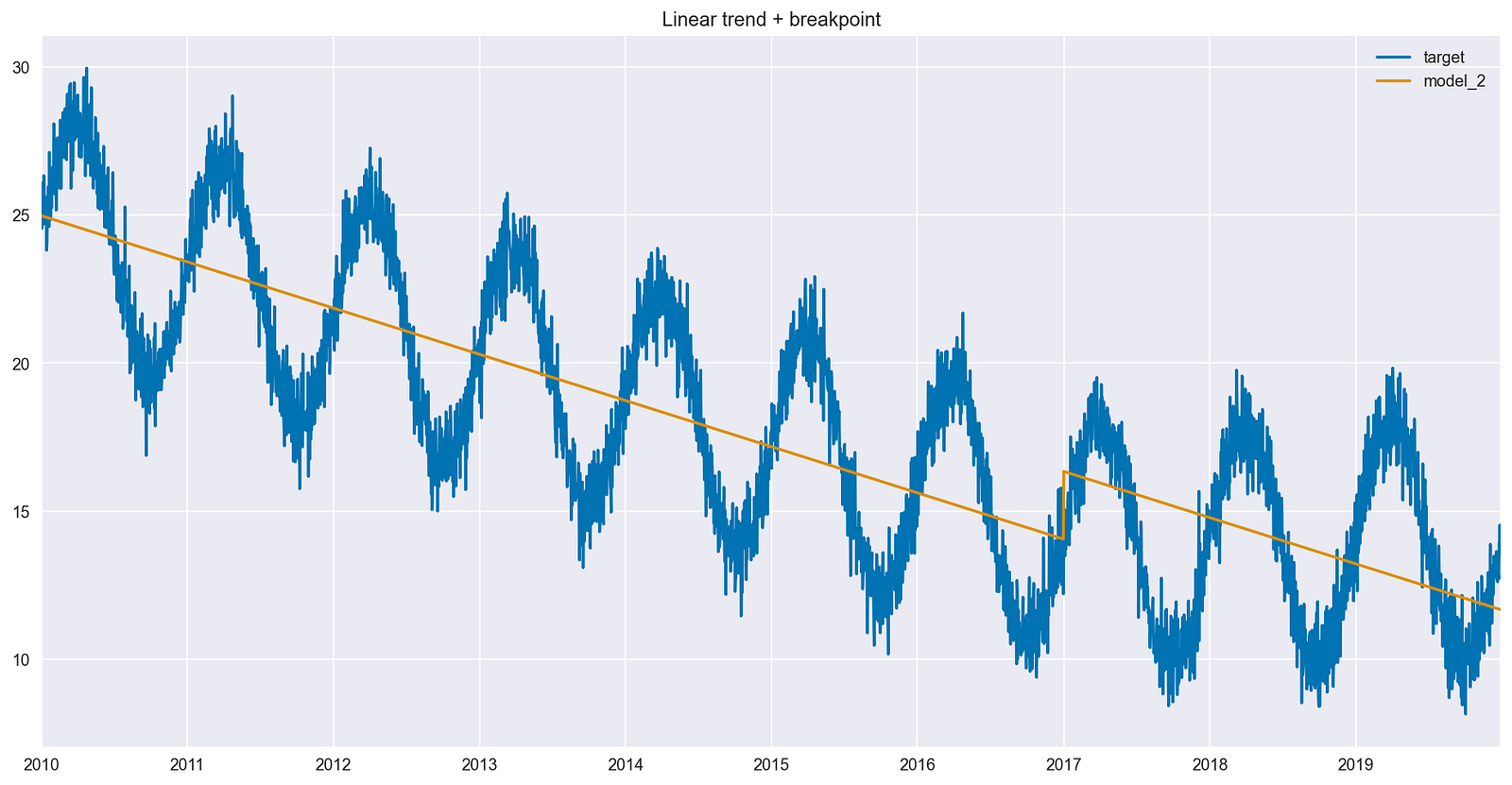
图 4 显示了一些重要的变化,如下所示:
- 拟合线显示垂直跳跃,该跳跃对应于新布尔特征的系数。
- 垂直跳跃恰好发生在功能激活的第一个日期(值为 1 而不是 0 )。
- 在引入断点之前和之后,直线的斜率是相同的。
- 该模型试图通过在断点后的预测中添加固定的量来补偿不正确的斜率。
在过去 3 年的数据中没有趋势,因此理想情况下, 2017 年 1 月 1 日之后,该线应接近持平。
添加交互项
要更改断点后的斜率,请添加一个更复杂的时间戳依赖项(用线性趋势表示)。这正是交互项的作用——它是线性趋势和占位符变量的乘积。
df["interaction_term"] = df["after_2017_breakpoint"] * df["linear_trend"]
X = df[["linear_trend", "after_2017_breakpoint", "interaction_term"]]
y = df[["target"]]
lm = LinearRegression()
lm.fit(X, y)
df["model_3"] = lm.predict(X)
df[["target", "model_3"]].plot(title="Linear trend + breakpoint + interaction term");
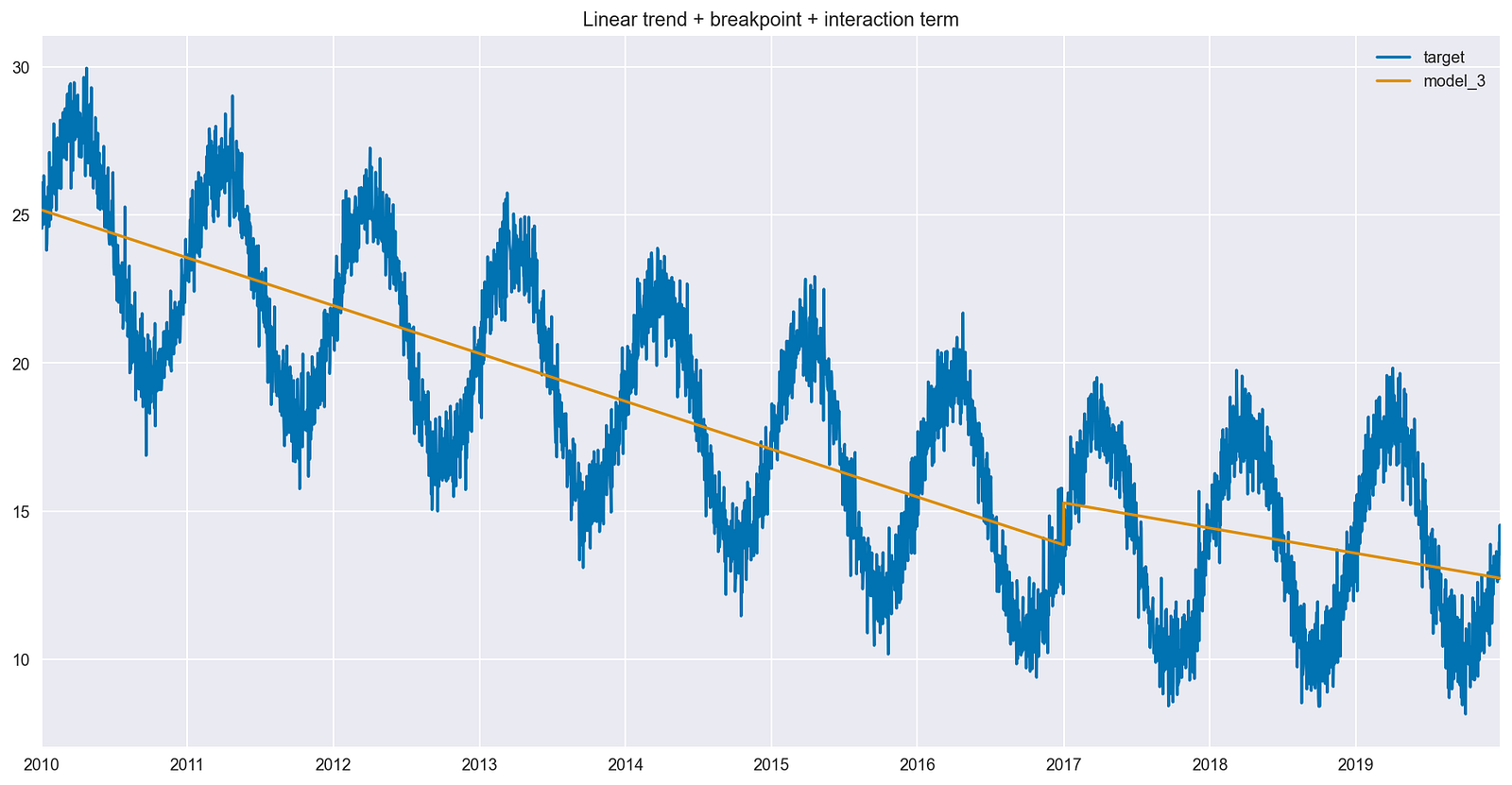
图 5 显示了在模型中使用交互项的影响。与图 4 相比,最佳拟合线在断点后的斜率不同。
更准确地说,差值实际上是相互作用项的系数值。虽然新线没有变平,但它仍然没有时间序列早期那么陡峭。
将断点与交互项一起引入,提高了模型捕捉时间序列趋势的能力。反过来,这应该会提高模型的预测性能。
总结
使用交互项可以使线性模型的规范更加灵活(不同线的斜率不同),从而更好地拟合数据并具有更好的预测性能。您可以将交互项添加为原始功能的乘积。在时间序列的上下文中,您可以使用交互术语来更好地捕捉趋势的任何变化。
您可以在此帖子中使用的代码“时间序列预测中交互项的全面指南”在 GitHub 上查找。此外,笔记本中的代码展示了如何利用 cuDF 和 cuML 使用 GPU 加速训练您的模型。我们欢迎您的反馈,您可以通过Twitter或在评论中联系我。