线性回归中相互作用项的综合指南

线性回归是一种强大的统计工具，用于对因变量和一个或多个自变量（特征）之间的关系进行建模。回归分析中一个重要且经常被遗忘的概念是交互作用项。简而言之，交互术语使您能够检查目标和自变量之间的关系是否会根据另一个自变量的值而变化。

交互术语是回归分析的一个关键组成部分，了解它们的工作原理可以帮助从业者更好地训练模型和解释数据。然而，尽管交互术语很重要，但它们可能很难理解。

这篇文章提供了线性回归背景下交互作用术语的直观解释。

回归模型中的交互项是什么？

首先，这是一个更简单的案例；也就是说，一个没有相互作用项的线性模型。这样的模型假设每个特征或预测器对因变量（目标）的影响独立于模型中的其他预测器。

以下等式描述了具有两个特征的此类模型规范：

$y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \epsilon$

为了使解释更容易理解，这里有一个例子。想象一下，你对房地产价格建模感兴趣 (y) 使用两个功能：它们的大小 (X1 个) 以及指示公寓是否位于市中心的布尔标志 (2 个) . $\beta_0$ 是截距， $\beta_1$ 和 $\beta_2$ 是线性模型的系数，以及 $\epsilon$ 是误差项（模型无法解释）。

在收集数据并估计线性回归模型后，可以获得以下系数：

$y = 300 + 20x_1 + 10x_2$

知道估计的系数和2 个是一个布尔功能，您可以根据的值写出两种可能的情况2 个.

市中心

$y = 310 + 20x_1$

市中心外

$y = 300 + 20x_1$

如何解读这些？虽然这在房地产领域可能没有多大意义，但你可以说，市中心一套 0 平方米的公寓的价格是 310 （截距的价值）。每增加一平方米的空间，价格就会上涨 20 。在另一种情况下，唯一的区别是截距小于 10 个单位。图 1 显示了两条最佳拟合线。

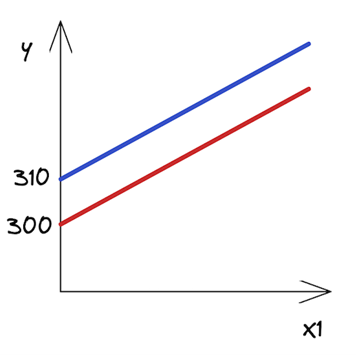
A line plot showing two best-fit lines running in parallel — *图 1 。市中心和城外房产的回归线*

正如你所看到的，这些线是平行的，它们有相同的斜率 — 系数由X1 个，这在两种情况下都是一样的。

交互作用术语表示联合效应

在这一点上，你可能会争辩说，在市中心的公寓里多住一平方米比在郊区的公寓里多花一平方米要贵。换句话说，这两个特征可能会对房地产价格产生共同影响。

所以，你认为不仅两种情况下的截距应该不同，而且直线的斜率也应该不同。如何做到这一点？这正是互动术语发挥作用的时候。它们使模型的规范更加灵活，并使您能够考虑到这些模式。

交互项实际上是你认为对目标有共同影响的两个特征的乘积。以下等式表示模型的新规范：

$y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3x_1x_2 + \epsilon$

再次假设你已经估计了你的模型，并且你知道系数。为了简单起见，我保留了与前面示例中相同的值。请记住，在现实生活中，它们可能会有所不同。

$y = 300 + 20x_1 + 10x_2 + 5x_1x_2$

市中心

$y = 310 + 25x_1$

市中心外

$y = 300 + 20x_1$

在你写出两个场景之后2 个（市中心或市中心外），您可以立即看到坡度（系数X1 个) 两条线中的一条不同。正如假设的那样，现在市中心增加一平方米的空间比郊区更贵。

用交互项解释系数

向模型中添加交互项会改变对所有系数的解释。如果没有交互项，则可以将系数解释为预测器对因变量的独特影响。

所以在这种情况下，你可以这么说 $\beta_1$ 是公寓大小对价格的独特影响。然而，对于交互项，公寓大小对不同值的影响是不同的2 个换句话说，公寓规模对价格的独特影响不再局限于 $\beta_1$ .

为了更好地理解每个系数代表什么，这里再看一看具有交互项的线性模型的原始规范。作为提醒，2 个是一个布尔特征，指示特定公寓是否位于市中心。

$y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3x_1x_2 + \epsilon$

现在，您可以通过以下方式解释每个系数：

$\beta_0$ : 拦截市中心以外的公寓（或布尔特征为零值的任何组2 个) .
$\beta_1$ : 市中心以外公寓的坡度（价格的影响）。
$\beta_2$ : 两组之间的截距差异。
$\beta_3$ : 市中心和城外公寓之间的坡度差异。

例如，假设你正在测试一个假设，即无论公寓是否在市中心，公寓的大小对价格的影响都是相等的。然后，您将使用交互项来估计线性回归，并检查 $\beta_3$ 与 0 显著不同。

关于交互术语的一些附加注释：

我提出了双向交互术语；然而，高阶相互作用（例如，三个特征的相互作用）也是可能的。
在这个例子中，我展示了一个数字特征（公寓的大小）与布尔特征（公寓在市中心吗？）的交互。但是，您也可以为两个数字特征创建交互项。例如，您可以创建一个公寓大小与房间数量的交互项。有关详细信息，请参阅相关资源部分。
这种情况下，相互作用项可能具有统计学意义，但主要影响并不显著。然后，你应该遵循分层原则，即如果你在模型中包括一个交互项，你也应该包括主要影响，即使它们的影响在统计上并不显著。

Python 中的实际操作示例

在所有的理论介绍之后，下面是如何在 Python 中为线性回归模型添加交互项。一如既往，首先导入所需的库。

import numpy as np
import pandas as pd

import statsmodels.api as sm
import statsmodels.formula.api as smf

# plotting
import seaborn as sns
import matplotlib.pyplot as plt

# settings
plt.style.use("seaborn-v0_8")
sns.set_palette("colorblind")
plt.rcParams["figure.figsize"] = (16, 8)
%config InlineBackend.figure_format = 'retina'

在本例中，您使用statsmodels图书馆对于数据集，使用mtcars数据集。我敢肯定，如果你曾经使用过 R ，你就会对这个数据集很熟悉。

首先，加载数据集：

mtcars = sm.datasets.get_rdataset("mtcars", "datasets", cache=True)
print(mtcars.__doc__)

执行代码示例将打印数据集的全面描述。在这篇文章中，我只展示了相关部分 — 列的总体描述和定义：

  ====== ===============
  mtcars R Documentation
  ====== ===============

数据摘自 1974 年的美国杂志MotorTrend，由 32 辆汽车（ 1973-74 车型）的油耗和汽车设计和性能的 10 个方面组成。

这是一个 DataFrame ，它对 11 个（数字）变量进行了 32 次观测：

  ===== ==== ========================================
  [, 1] mpg  Miles/(US) gallon
  [, 2] cyl  Number of cylinders
  [, 3] disp Displacement (cu.in.)
  [, 4] hp   Gross horsepower
  [, 5] drat Rear axle ratio
  [, 6] wt   Weight (1000 lbs)
  [, 7] qsec 1/4 mile time
  [, 8] vs   Engine (0 = V-shaped, 1 = straight)
  [, 9] am   Transmission (0 = automatic, 1 = manual)
  [,10] gear Number of forward gears
  [,11] carb Number of carburetors
  ===== ==== ========================================

然后，从加载的对象中提取实际数据集：

df = mtcars.data
df.head()

	英里/加仑	气缸	显示	马力	德拉特	重量	质量安全委员会	对	是	排挡	碳水化合物
马自达 RX4	21	6	160	110	3 . 90	2 . 620	16 . 46	0	1	4	4
马自达 RX4 Wag	21	6	160	110	3 . 90	2 . 875	17 . 02	0	1	4	4
达特桑 710	22 . 8	4	108	93	3 . 85	2 . 320	18 . 61	1	1	4	1
大黄蜂 4 号驱动器	21 . 4	6	258	110	3 . 08	3 . 215	19 . 44	1	0	3	1
大黄蜂运动型	18 . 7	8	360	175	3 . 15	3 . 440	17 . 02	0	0	3	2

表 1 。的预览动车组数据集

对于这个例子，假设你想调查每加仑英里数之间的关系 (mpg) 和两个特征：重量 (wt，连续）和变速器类型 (am，布尔值）。

首先，绘制数据以获得一些初步见解：

sns.lmplot(x="wt", y="mpg", hue="am", data=df, fit_reg=False)
plt.ylabel("Miles per Gallon")
plt.xlabel("Vehicle Weight");

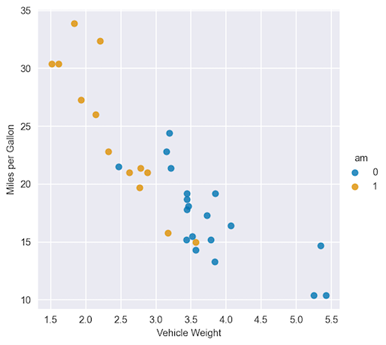
Scatterplot showing different patterns for the two transmission types. — *图 2 :每加仑英里数与车辆重量、每种变速器类型颜色的散点图*

通过观察图 2 ，您可以看到 am 变量的两个类别的回归线将大不相同。为了进行比较，从一个没有交互项的模型开始。

model_1 = smf.ols(formula="mpg ~ wt + am", data=df).fit()
model_1.summary()

下表显示了在没有交互项的情况下拟合线性回归的结果。

OLS Regression Results                       	 
==============================================================================
Dep. Variable:                	  mpg   	R-squared:             	0.753
Model:                        	  OLS      Adj. R-squared:             	0.736
Method:                 Least Squares         F-statistic:             	44.17
Date:                Sat, 22 Apr 2023  Prob (F-statistic):           1.58e-09
Time:                        23:15:11      Log-Likelihood:            -80.015
No. Observations:              	   32   	      AIC:      	166.0
Df Residuals:                  	   29  	              BIC:          	170.4
Df Model:           	            2                                    	 
Covariance Type:            nonrobust                                    	 
==============================================================================
               coef     std err         t      P>|t|       [0.025       0.975]
------------------------------------------------------------------------------
Intercept   37.3216  	  3.055    12.218      0.000       31.074  	43.569
wt          -5.3528  	  0.788    -6.791      0.000       -6.965  	-3.741
am          -0.0236  	  1.546    -0.015      0.988       -3.185        3.138
==============================================================================
Omnibus:                    	3.009   Durbin-Watson:                  1.252
Prob(Omnibus):                  0.222   Jarque-Bera (JB):            	2.413
Skew:                       	0.670   Prob(JB):                    	0.299
Kurtosis:                   	2.881   Cond. No.                      21.7
==============================================================================

从汇总表中可以看出， am 特征的系数在统计上并不显著。使用您已经学习的系数的解释，您可以为 am 特征的两类绘制最佳拟合线。

X = np.linspace(1, 6, num=20)
sns.lmplot(x="wt", y="mpg", hue="am", data=df, fit_reg=False)
plt.title("Best fit lines for from the model without interactions")
plt.ylabel("Miles per Gallon")
plt.xlabel("Vehicle Weight")
plt.plot(X, 37.3216 - 5.3528 * X, "blue")
plt.plot(X, (37.3216 - 0.0236) - 5.3528 * X, "orange");

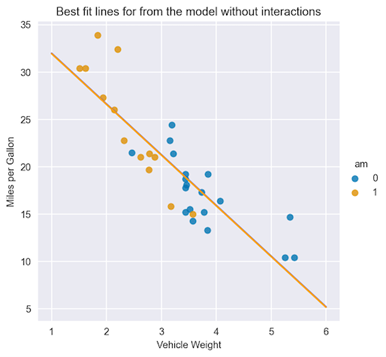
Scatterplot shows overlapping best fit lines for both transmission types. — *图 3 。两种变速器的最佳匹配线路*

图 3 显示了线条几乎重叠，因为 am 特征的系数基本为零。

接下来是第二个模型，这一次是两个功能之间的交互项。以下是如何在statsmodels公式

model_2 = smf.ols(formula="mpg ~ wt + am + wt:am", data=df).fit()
model_2.summary()

以下汇总表显示了用交互项拟合线性回归的结果。

OLS Regression Results                       	 
==============================================================================
Dep. Variable:                	 mpg      R-squared:                  0.833
Model:                        	 OLS      Adj. R-squared:             0.815
Method:                Least Squares      F-statistic:               46.57
Date:               Mon, 24 Apr 2023      Prob (F-statistic):         5.21e-11
Time:                       21:45:40      Log-Likelihood:           -73.738
No. Observations:              	  32      AIC:                      155.5
Df Residuals:                  	  28      BIC:                      161.3
Df Model:                          3                                    	 
Covariance Type:           nonrobust                                    	 
===============================================================================
                coef     std err         t      P>|t|       [0.025       0.975]
------------------------------------------------------------------------------
Intercept    31.4161  	   3.020    10.402  	0.000  	    25.230  	 37.602
wt           -3.7859  	   0.786    -4.819  	0.000  	    -5.395  	 -2.177
am           14.8784  	   4.264     3.489  	0.002        6.144  	 23.613
wt:am        -5.2984  	   1.445    -3.667  	0.001  	    -8.258  	 -2.339
==============================================================================
Omnibus:                    	3.839   Durbin-Watson:               	1.793
Prob(Omnibus):              	0.147   Jarque-Bera (JB):            	3.088
Skew:                       	0.761   Prob(JB):                    	0.213
Kurtosis:                   	2.963   Cond. No.                      40.1
==============================================================================

以下是您可以从具有交互项的汇总表中快速得出的两个结论：

所有的系数，包括相互作用项，都具有统计学意义。
通过检查 R2 （及其调整后的变体，因为模型中有不同数量的功能），您可以声明具有交互项的模型会产生更好的拟合。

与前面的情况类似，绘制最佳拟合线：

X = np.linspace(1, 6, num=20)
sns.lmplot(x="wt", y="mpg", hue="am", data=df, fit_reg=False)
plt.title("Best fit lines for from the model with interactions")
plt.ylabel("Miles per Gallon")
plt.xlabel("Vehicle Weight")
plt.plot(X, 31.4161 - 3.7859 * X, "blue")
plt.plot(X, (31.4161 + 14.8784) + (-3.7859 - 5.2984) * X, "orange");

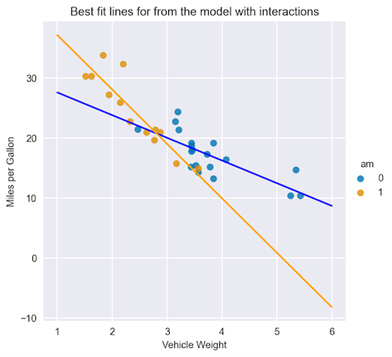
By using interaction terms, you get significantly different best fit lines for cars with automatic and manual transmissions. — *图 4 。两种类型变速器的最佳匹配线路，包括相互作用项*

在图 4 中，您可以立即看到配备自动变速器和手动变速器的汽车在截距和坡度方面的拟合线差异。

这里有一个好处：您还可以使用添加交互术语scikit-learn的PolynomialFeaturestransformer 不仅提供了添加任意阶的交互项的可能性，而且还创建了多项式特征（例如，可用特征的平方值）。有关详细信息，请参阅sklearn.preprocessing.PolynomialFeatures.

结束语

在处理线性回归中的交互项时，需要记住以下几点：

交互术语使您能够检查目标和功能之间的关系是否会根据另一个功能的值而变化。
添加交互项作为原始特征的乘积。通过将这些新变量添加到回归模型中，可以测量它们与目标之间相互作用的效果。仔细解释相互作用项的系数对于理解关系的方向和强度至关重要。
通过使用交互项，可以使线性模型的规范更加灵活（不同线的斜率不同），从而更好地拟合数据并具有更好的预测性能。

你可以在我的/erykmlGitHub 查看代码。一如既往，任何建设性的反馈都是非常受欢迎的。

线性回归中相互作用项的综合指南

回归模型中的交互项是什么？

交互作用术语表示联合效应

用交互项解释系数

Python 中的实际操作示例

结束语

Tags

关于作者

线性回归中相互作用项的综合指南

回归模型中的交互项是什么？

交互作用术语表示联合效应

用交互项解释系数

Python 中的实际操作示例

结束语

相关资源

Tags

关于作者

Related posts

在 LLM 架构中应用多专家模型

cuTENSOR 2.0：用于加速张量计算的全面指南

cuTENSOR 2.0：应用程序和性能

聚焦：Honeywell 借助 NVIDIA cuDSS 加速工业流程仿真

新视频：开创性的气候技术和缓解自然灾害影响