Tensor contractions are at the core of many important workloads in machine learning, computational chemistry, and quantum computing. As scientists and engineers pursue ever-growing problems, the underlying data gets larger in size and calculations take longer and longer.
When a tensor contraction does not fit into a single GPU anymore, or if it takes too long on a single GPU, the natural next step is to distribute the contraction across multiple GPUs. We have been extending cuTENSOR with this new capability, and are releasing it as a new library called cuTENSORMg (multi-GPU). It provides single-process multi-GPU functionality on block-cyclic distributed tensors.
The copy and contraction operations for cuTENSORMg are broadly structured into handles, tensor descriptors, and descriptors. In this post, we explain the handle and the tensor descriptor and how copy operations work and demonstrate how to perform a tensor contraction. We then show how to measure the performance of the contraction operation for various workloads and GPU configurations.
Library handle
The library handle represents the set of devices that participate in the computation. The handle also contains data and resources that are reused across calls. You can create a library handle by passing the list of devices to the cutensorMgCreate function:
cutensorMgCreate(&handle, numDevices, devices);
All objects in cuTENSORMg are heap allocated. As such, they must be freed with a matching destroy call. For brevity, we do not show these in this post, but production code should destroy all objects that it creates to avoid leaks.
cutensorMgDestroy(handle);All library calls return an error code of type cutensorStatus_t. In production, you should always check the error code to detect failures or usage issues early. For brevity, we omit these checks in this post for brevity, but they are included in the corresponding example code.
In addition to error codes, cuTENSORMg also provides similar logging capabilities as cuTENSOR. Those logs can be activated by setting the CUTENSORMG_LOG_LEVEL environment variable appropriately. For instance, CUTENSORMG_LOG_LEVEL=1 would provide you with additional information about a returned error code.
Tensor descriptor
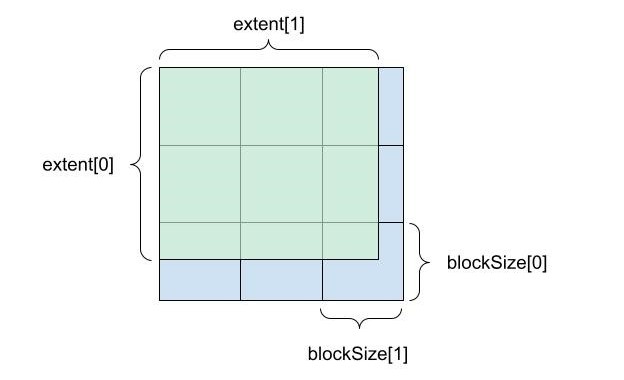
The tensor descriptor describes how a tensor is laid out in memory and how it is distributed across devices. For each mode, there are three core concepts to determine the layout:
extent: Logical size of each mode.blockSize: Subdivides theextentinto equal-sized chunks, except for the final remainder block.deviceCount: Determines how the blocks are distributed across devices.
Figure 1 shows how extent and block size subdivide a two-dimensional tensor.
![A 3x3 square showing deviceCount [0] on the Y axis and deviceCount[1] on the X axis.](https://developer-blogs.nvidia.com/wp-content/uploads/2022/03/Introducing-Multi-GPU-Tensor-Contractions-4-625x494_2.jpg)
Blocks are distributed in a cyclic fashion, which means that consecutive blocks are assigned to different devices. Figure 2 shows a two-by-two distribution of blocks to devices, with the assignment of devices to blocks being encoded with another array devices. The array is a dense-column major tensor with extents like the device counts.
![A 4x4 block with Y axis as blockStride[0] and X axis blockStride[1]. This block is comprised of smaller by 4x4 blocks with elementStride[1] as the X axis and and elementStride[0] as the Y axis.](https://developer-blogs.nvidia.com/wp-content/uploads/2022/03/Introducing-Multi-GPU-Tensor-Contractions-2-625x469_2.jpg)
Finally, the exact on-device data layout is determined by the elementStride and the blockStride values for each mode. Respectively, they determine the displacement, in linear memory in units of elements, of two adjacent elements and adjacent blocks for a given mode (Figure 3).
These attributes are all set using the cutensorMgCreateTensorDescriptor call:
cutensorMgCreateTensorDescriptor(handle, &desc, numModes, extent, elementStride, blockSize, blockStride, deviceCount, numDevices, devices, type);
It is possible to pass NULL to the elementStride, blockSize, blockStride, and deviceCount.
If the elementStride is NULL, the data layout is assumed to be dense using a generalized column-major layout. If blockSize is NULL, it is equal to extent. If blockStride is NULL, it is equal to blockSize * elementStride, which results in an interleaved block format. If deviceCount is NULL, all device counts are set to 1. In this case, the tensor is distributed and entirely resides in the memory of devices[0].
By passing CUTENSOR_MG_DEVICE_HOST as the owning device, you can specify that the tensor is located on the host in pinned, managed, or regularly allocated memory.
Copy operation
The copy operation enables data layout changes including the redistribution of the tensor to different devices. Its parameters are a source and a destination tensor descriptor (descSrc and descDst), as well as a source and destination mode list (modesSrc and modesDst). The two tensors’ extents at coinciding modes must match, but everything else about them may be different. One may be located on the host, the other across devices, and they may have different blockings and different strides.
Like all operations in cuTENSORMg, it proceeds in three steps:
cutensorMgCopyDescriptor_t: Encodes what operation should be performed.cutensorMgCopyPlan_t: Encodes how the operation will be performed.cutensorMgCopy: Performs the operation according to the plan.
The first step is to create the copy descriptor:
cutensorMgCreateCopyDescriptor(handle, &desc, descDst, modesDst, descSrc, modesSrc);With the copy descriptor in hand, you can query the amount of device-side and host-side workspace that is required. The deviceWorkspaceSize array has as many elements as there are devices in the handle. The i-th element is the amount of workspace required for the i-th device in the handle.
cutensorMgCopyGetWorkspace(handle, desc, deviceWorkspaceSize, &hostWorkspaceSize);
With the workspace sizes determined, plan the copy. You can pass a larger workspace size and the call may take advantage of more workspace, or you can try to pass a smaller size. The planning may be able to accommodate that or it may yield an error.
cutensorMgCreateCopyPlan(handle, &plan, desc, deviceWorkspaceSize, hostWorkspaceSizeFinally, with the planning complete, execute the copy operation.
cutensorMgCopy(handle, plan, ptrDst, ptrSrc, deviceWorkspace, hostWorkspace, streams);In this call, ptrDst and ptrSrc are arrays of pointers. They contain one pointer for each of the devices in the corresponding tensor descriptor. In this instance, ptrDst[0] corresponds to the device that was passed as devices[0] to cutensorMgCreateTensorDescriptor.
On the other hand, deviceWorkspace and streams are also arrays where each entry corresponds to a device. They are ordered according to the order of devices in the library handle, such as deviceWorkspace[0] and streams[0] correspond to the device that was passed at devices[0] to cutensorMgCreate. The workspaces must be at least as large as the workspace sizes that were passed to cutensorMgCreateCopyPlan.
Contraction operation
At the core of the cuTENSORMg library is the contraction operation. It currently implements tensor contractions of tensors located on one or multiple devices, but may support tensors located on the host in the future. As a refresher, a contraction is an operation of the following form:
Where ,
,
, and
are tensors, and
,
,
, and
are mode lists that may be arbitrarily permuted and interleaved with each other.
Like the copy operation, it proceeds in three stages:
cutensorMgCreateContractionDescriptor: Encodes the problem.cutensorMgCreateContractionPlan: Encodes the implementation.cutensorMgContraction: Uses the plan and performs the actual contraction.
First, you create a contraction descriptor based on the tensor descriptors, mode lists, and the desired compute type, such as the lowest precision data that may be used during the calculation.
cutensorMgCreateContractionDescriptor(handle, &desc, descA, modesA, descB, modesB, descC, modesC, descD, modesD, compute);
As the contraction operation has more degrees of freedom, you must also initialize a find object that gives you finer control over the plan creation for a given problem descriptor. For now, this find object only has a default setting:
cutensorMgCreateContractionFind(handle, &find, CUTENSORMG_ALGO_DEFAULT);
Then, you can query the workspace requirement along the lines of what you did for the copy operation. Compared to that operation, you also pass in the find and a workspace preference:
cutensorMgContractionGetWorkspace(handle, desc, find, CUTENSOR_WORKSPACE_RECOMMENDED, deviceWorkspaceSize, &hostWorkspaceSize);
Create a plan:
cutensorMgCreateContractionPlan(handle, &plan, desc, find, deviceWorkspaceSize, hostWorkspaceSize);
Finally, execute the contraction using the plan:
cutensorMgContraction(handle, plan, alpha, ptrA, ptrB, beta, ptrC, ptrD, deviceWorkspace, hostWorkspace, streams);
In this call, alpha and beta are host pointers of the same type as the tensor, unless the
tensor is half or
BFloat16 precision, in which case it is single precision. The order of pointers in the different arrays ptrA, ptrB, ptrC, and ptrD correspond to their order in their descriptor’s devices array. The order of pointers in the deviceWorkspace and streams arrays corresponds to the order in the library handle’s devices array.
Performance
You can find all these calls together in the CUDA Library Samples GitHub repo. We extended it to take two parameters: The number of GPUs and a scaling factor. Feel free to experiment with other contractions, block sizes, and scaling regimes. It is written in such a way that it scales up M and N while keeping K fixed. It implements an almost GEMM-shaped tensor contraction of the shape:
and
scale up and the block size in those dimensions keeping the load approximately balanced. The plot underneath shows their scaling relationship when measured on a DGX A100.
Get started with cuTENSORMg
Interested in trying out cuTENSORMg to scale tensor contractions beyond a single GPU?
We continue working on improving cuTENSORMg, including out-of-core functionality. If you have questions or new feature requests, contact product manager Matthew Nicely US.