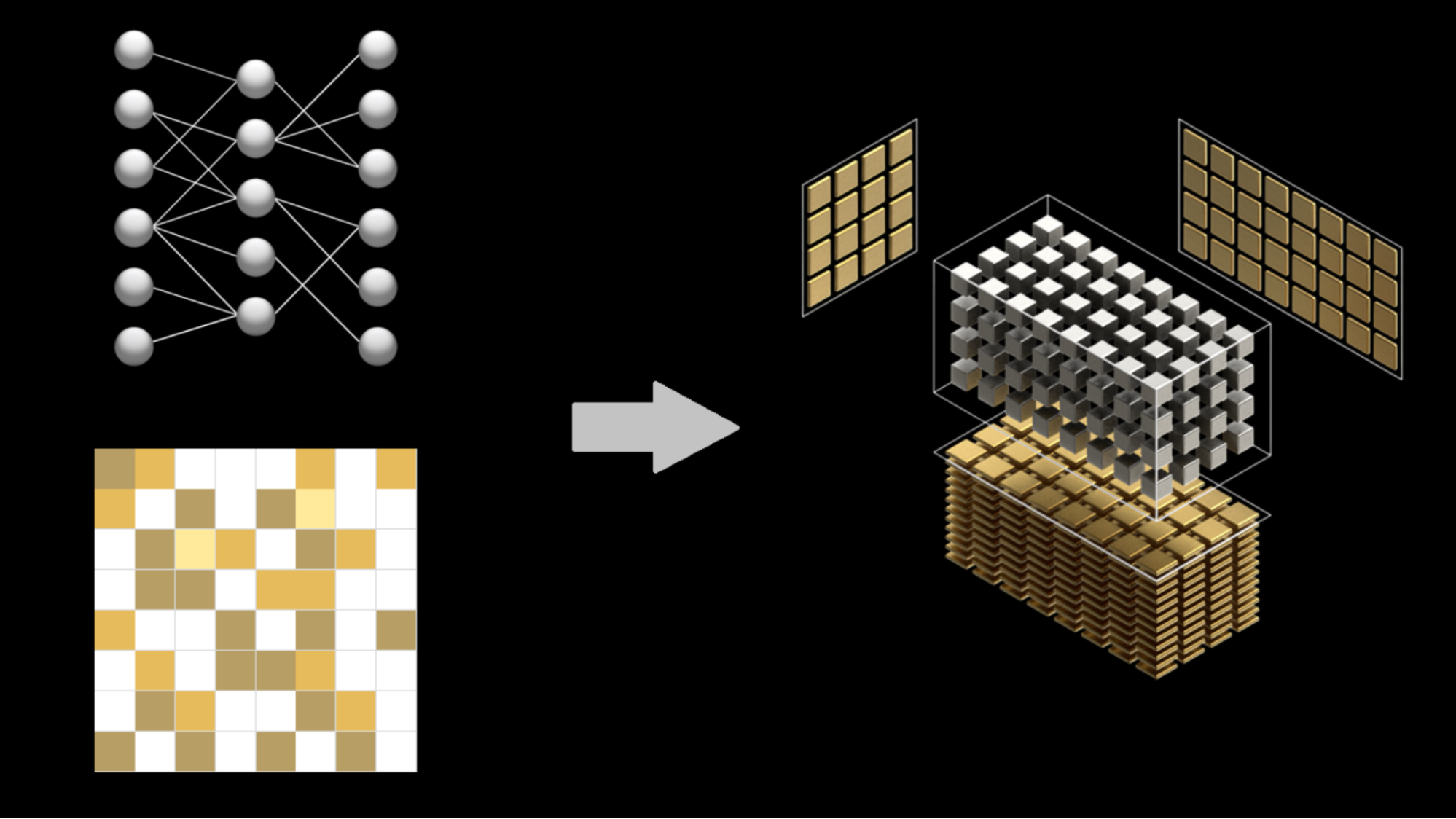
Deep neural networks achieve outstanding performance in a variety of fields, such as computer vision, speech recognition, and natural language processing. The computational power needed to process these neural networks is rapidly increasing, so efficient models and computation are crucial. Neural network pruning, removing unnecessary model parameters to yield a sparse network, is a useful way to reduce model complexity while maintaining accuracy.
To exploit fine-grained network pruning, the NVIDIA Ampere GPU architecture introduces the concept of fine-grained structured sparsity. On the NVIDIA A100 GPU, the structure manifests as a 2:4 pattern: out of every four elements, at least two must be zero. This reduces the data footprint and bandwidth of one matrix multiply (also known as GEMM) operand by 2x and doubles throughput by skipping the computation of the zero values using new NVIDIA Sparse Tensor Cores.
cuSPARSELt: A high-performance CUDA library for sparse matrix-dense matrix multiplication
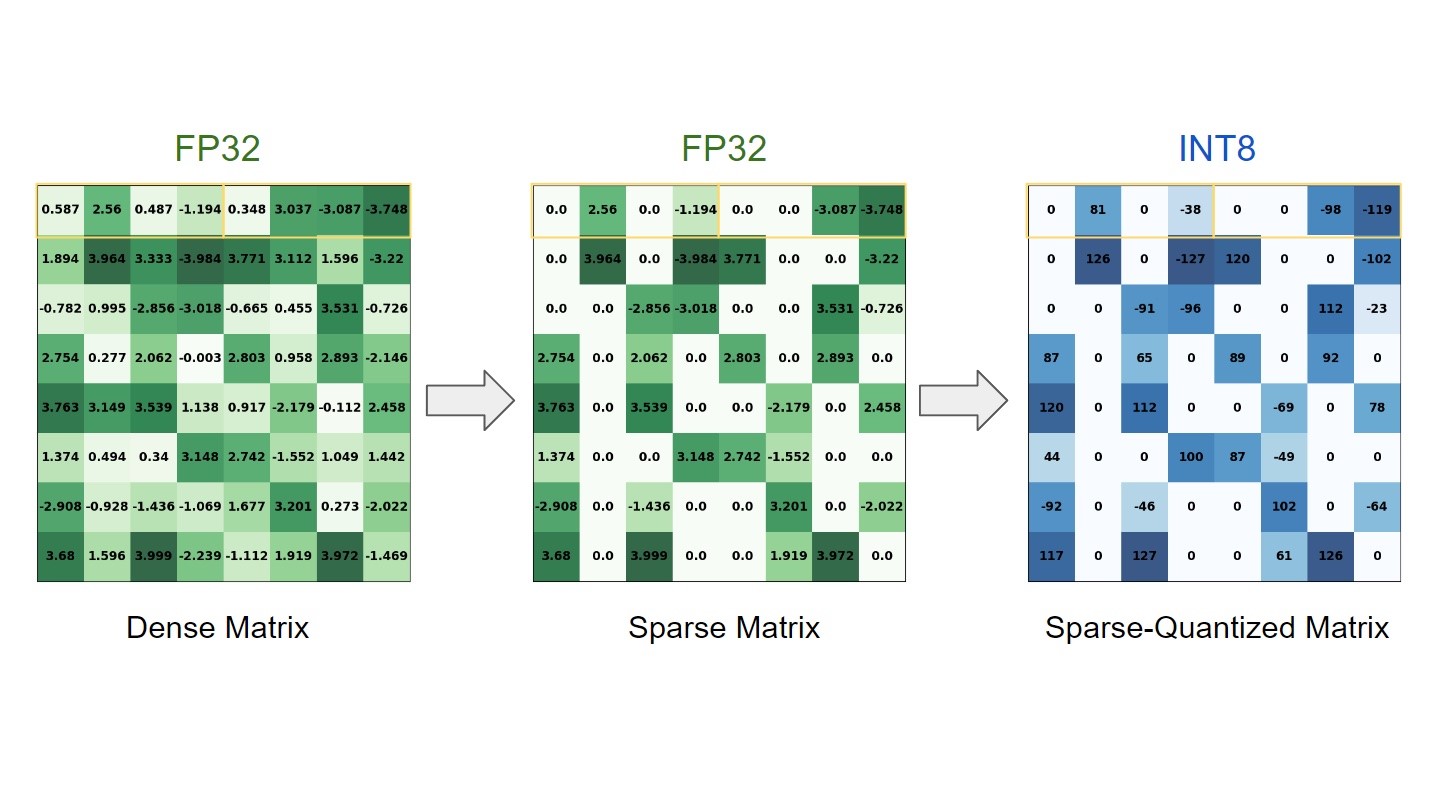
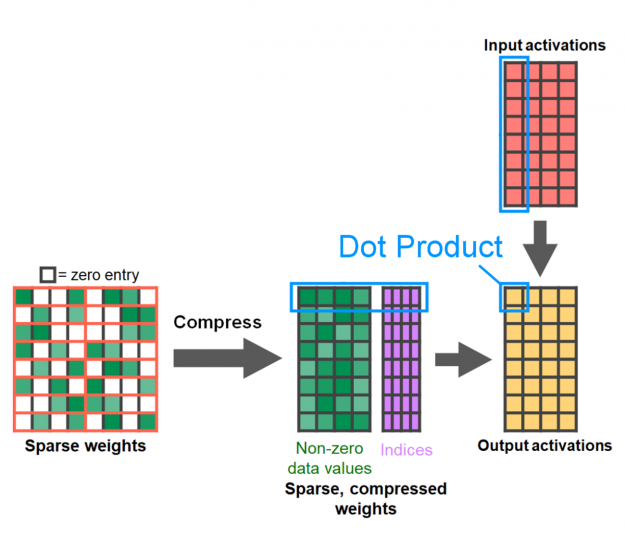
Figure 2 shows how NVIDIA Sparse Tensor Cores operate on only half of one input to double the math efficiency. On the left is a weight matrix pruned to meet the expected 2:4 sparse pattern. As you can see, in each group of four weights (outlined in orange), only two weights are nonzero (shades of green). This matrix is compressed to be half the size of the original matrix with a small amount of metadata to keep track of where the nonzeros were in the original, uncompressed matrix. This metadata is used to select only the corresponding activations from the second input matrix, letting the NVIDIA Sparse Tensor Core skip computing multiplications by zero to achieve twice the throughput of a regular Tensor Core.
To make it easy to use NVIDIA Ampere architecture sparse capabilities, NVIDIA introduces cuSPARSELt, a high-performance CUDA library dedicated to general matrix-matrix operations in which at least one operand is a sparse matrix. The cuSPARSELt library lets you use NVIDIA third-generation Tensor Cores Sparse Matrix Multiply-Accumulate (SpMMA) operation without the complexity of low-level programming. The library also provides helper functions for pruning and compressing matrices.
The key features of cuSPARSELt include the following:
- NVIDIA Sparse Tensor Core support
- Mixed-precision support:
FP16inputs/output,FP32Tensor Core accumulationBFLOAT16inputs/output,FP32Tensor Core accumulationINT8inputs/output,INT32Tensor Core accumulation
- Row-major and column-major memory layouts
- Matrix pruning and compression utilities
- Auto-tuning functionality
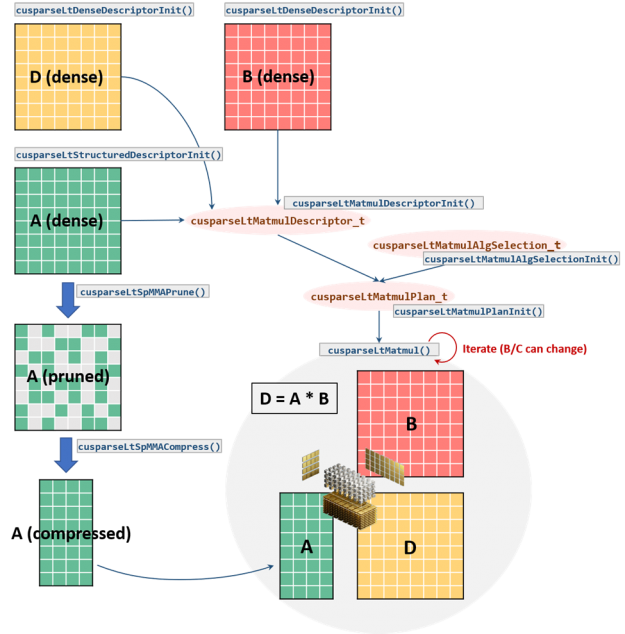
cuSPARSELt workflow
The cuSPARSELt library follows an equivalent approach and adopts similar concepts to cuBLASLt and cuTENSOR. The library programming model requires organizing the computation in such a way that the same setup can be repeatedly used for different inputs.
In particular, the model relies on the following high-level stages:
- Problem definition: Specify matrix shapes, data types, operations, and so on.
- User preferences and constraints: Provide an algorithm selection or limit the search space of viable implementations (candidates).
- Plan: Gather descriptors for the execution and “find” the best implementation if needed.
- Execution: Perform the actual computation.
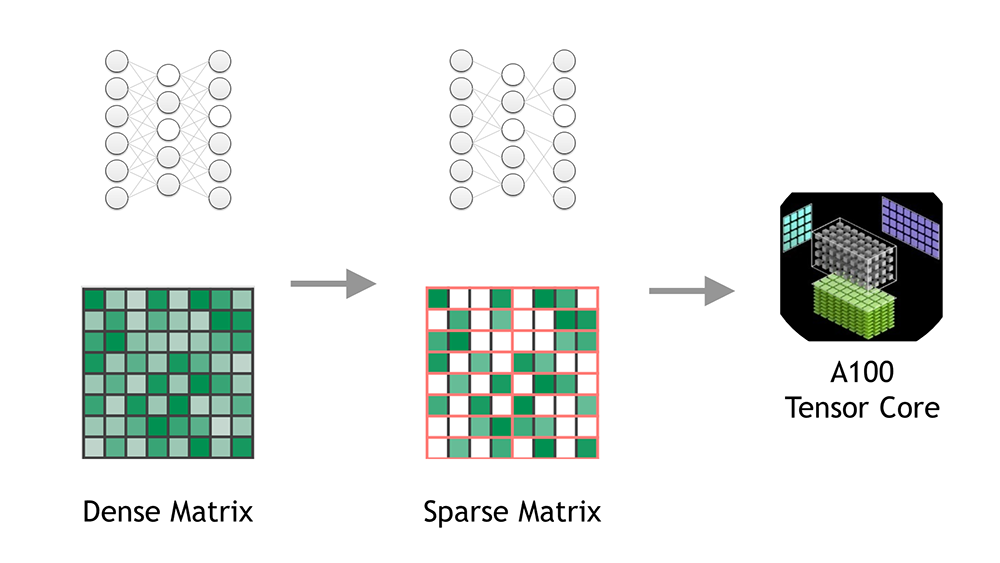
The common workflow consists of the following steps (Figure 3):
- Initialize the library handle:
cusparseLtInit. - Specify the input/output matrix characteristics:
cusparseLtDenseDescriptorInit,cusparseLtStructuredDescriptorInit. - Initialize the matrix multiplication descriptor and its properties (e.g. operations, compute type, etc.):
cusparseLtMatmulDescriptorInit. - Initialize the algorithm selection descriptor:
cusparseLtMatmulAlgSelectionInit. - Initialize the matrix multiplication plan:
cusparseLtMatmulPlanInit. - Prune the A matrix:
cusparseLtSpMMAPrune. This step is not needed if the user provides a matrix that already satisfies the 2:4 structured sparsity constraint, such as a weight matrix generated by the ASP library. - Compress the pruned matrix:
cusparseLtSpMMACompress. - Execute the matrix multiplication:
cusparseLtMatmul. This step can be repeated multiple times with different inputs. - Destroy the matrix multiplication plan and the library handle:
cusparseLtMatmulPlanDestroy,cusparseLtDestroy.
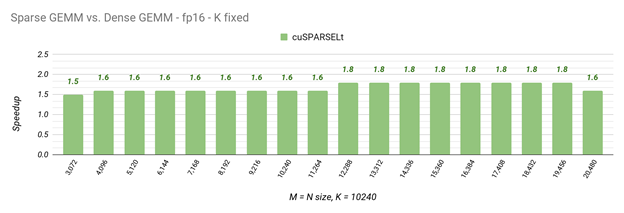
Sparse GEMM Performance
As with dense matrix multiplication, the performance of sparse matrix multiplications varies with GEMM dimensions, layouts, and data types. Here’s a snapshot of the relative performance of dense and sparse GEMMs with today’s software.
The following charts show the performance of the cuSPARSELt and cuBLAS for the following operation:
D=alpha*op(A)*op(B)+beta*C
In this operation, A , B , and D=C are dense matrices of sizes MxK, KxN, and MxN, respectively. We denote the layouts of the matrices A and B with N for column-major order (op is non-transposed) and T for row-major order (op is transposed).
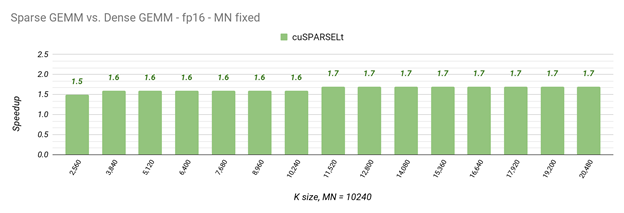
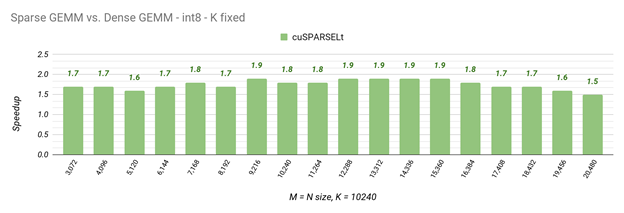
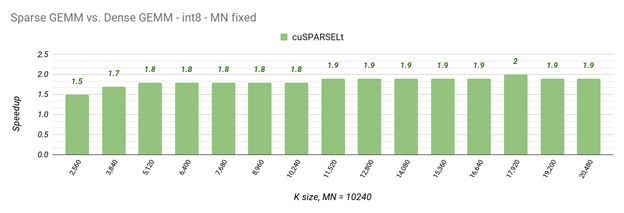
To showcase the performance achievable with cuSPARSELt for a real workload, the following table shows some common GEMM sizes used by a pruned BERT-Large model (seqlen=128, BS=128) with column-major TN FP16 kernels. In general, the larger the workload is, the more that sparsity can help.
| Layer | M | N | K | Dense TFLOPs | Sparse TFLOPs | Speedup |
| QKV | 3072 | 16384 | 1024 | 188 | 263 | 1.4x |
| PROJ | 1024 | 16384 | 1024 | 183 | 242 | 1.3x |
| FC1 | 4096 | 16384 | 1024 | 196 | 270 | 1.4x |
| FC2 | 1024 | 16384 | 4096 | 211 | 339 | 1.6x |
Structured sparse matrix-matrix multiplication code example
Now that you’ve seen the available performance, here’s an example of performing a matrix multiplication with structured sparsity in the cuSPARSELt library using Sparse Tensor Cores in the NVIDIA A100 or GA100 GPU. For more information, see the NVIDIA/CUDALibrarySamples/tree/master/cuSPARSELt/spmma GitHub repo.
First, include the cuSPARSELt header, set up some device pointers and data structures, and initialize the cuSPARSELt handle.
#include <cusparseLt.h> // cusparseLt header // Device pointers and coefficient definitions float alpha = 1.0f; float beta = 0.0f; __half* dA = ... __half* dB = ... __half* dC = ... // cusparseLt data structures and handle initialization cusparseLtHandle_t handle; cusparseLtMatDescriptor_t matA, matB, matC; cusparseLtMatmulDescriptor_t matmul; cusparseLtMatmulAlgSelection_t alg_sel; cusparseLtMatmulPlan_t plan; cudaStream_t stream = nullptr; cusparseLtInit(&handle);
Next, initialize the structured sparse input matrix (matrix A), dense input matrix (matrix B), and dense output matrix (matrix C) descriptors.
cusparseLtStructuredDescriptorInit(&handle, &matA, num_A_rows, num_A_cols, lda, alignment, type, order, CUSPARSELT_SPARSITY_50_PERCENT); cusparseLtDenseDescriptorInit(&handle, &matB, num_B_rows, num_B_cols, ldb, alignment, type, order); cusparseLtDenseDescriptorInit(&handle, &matC, num_C_rows, num_C_cols, ldc, alignment, type, order);
With the descriptors ready, you can prepare the matrix multiplication operation’s descriptor, select an algorithm to use to perform the matmul operation, and initialize the matmul plan.
cusparseLtMatmulDescriptorInit(&handle, &matmul, opA, opB, &matA, &matB, &matC, &matC, compute_type); cusparseLtMatmulAlgSelectionInit(&handle, &alg_sel, &matmul, CUSPARSELT_MATMUL_ALG_DEFAULT); int alg = 0; // set algorithm ID cusparseLtMatmulAlgSetAttribute(&handle, &alg_sel, CUSPARSELT_MATMUL_ALG_CONFIG_ID, &alg, sizeof(alg)); size_t workspace_size, compressed_size; cusparseLtMatmulGetWorkspace(&handle, &alg_sel, &workspace_size); cusparseLtMatmulPlanInit(&handle, &plan, &matmul, &alg_sel, workspace_size);
If the sparse matrix hasn’t been pruned by another process, you can do it at this point. Don’t forget to check the validity of the sparsity pattern to make sure it can be accelerated with Sparse Tensor Cores.
cusparseLtSpMMAPrune(&handle, &matmul, dA, dA, CUSPARSELT_PRUNE_SPMMA_TILE,
stream);
// checking the correctness
int is_valid = 0;
cusparseLtSpMMAPruneCheck(&handle, &matmul, dA, &is_valid, stream);
if (is_valid != 0) {
std::printf("!!!! The matrix does not conform to the SpMMA sparsity pattern. "
"cusparseLtMatmul does not provide correct results\n");
return EXIT_FAILURE;
}
Now that matrix A has been pruned with 2:4 sparsity, you can compress it to roughly half of its original size. This execution time for this step is negligible compared to the actual matrix multiplication (less than 5%).
cusparseLtSpMMACompressedSize(&handle, &plan, &compressed_size); cudaMalloc((void**) &dA_compressed, compressed_size); cusparseLtSpMMACompress(&handle, &plan, dA, dA_compressed, stream);
With the setup complete, perform the matmul operation. The call to cusparseLtMatmul can be repeated many times with different B matrices. You only have to set up the sparse matrix one time. For use cases where the A matrix values change, the cusparseLtSpMMACompress routine must be called again to set up the data structures for the sparse matrix.
void* d_workspace = nullptr; int num_streams = 0; cudaStream_t* streams = nullptr; cusparseLtMatmul(&handle, &plan, &alpha, dA_compressed, dB, &beta, dC, dD, d_workspace, streams, num_streams) )
Finally, clean up the used memory by destroying the matmul plan and cuSPARSELt handle.
cusparseLtMatmulPlanDestroy(&plan); cusparseLtDestroy(&handle);
Get started with cuSPARSELt
The cuSPARSELt library makes it easy to exploit NVIDIA Sparse Tensor Core operations, significantly improving the performance of matrix-matrix multiplication for deep learning applications without reducing network’s accuracy. The library also provides utilities for matrix compression, pruning, and performance auto-tuning. In short, cuSPARSELt reduces computation, power consumption, execution time, and memory storage compared to the common dense math approach.
The latest version of cuSPARSELt with NVIDIA Ampere architecture support can be found in NVIDIA GPU Accelerated Libraries. For more information about APIs, installation notes, new features, and examples, see cuSPARSELt: A High-Performance CUDA Library for Sparse Matrix-Matrix Multiplication.
For more information, see the following resources: