CUTLASS: Fast Linear Algebra in CUDA C++

Matrix multiplication is a key computation within many scientific applications, particularly those in deep learning. Many operations in modern deep neural networks are either defined as matrix multiplications or can be cast as such.
As an example, the NVIDIA cuDNN library implements convolutions for neural networks using various flavors of matrix multiplication. Matrix multiplication is also the core routine when computing convolutions based on Fast Fourier Transforms (FFT). When constructing cuDNN, NVIDIA started from high-performance implementations of general matrix multiplication (GEMM) in the cuBLAS library, supplementing and tailoring them to efficiently compute convolution. Today, the ability to adapt these GEMM strategies and algorithms is critical to delivering the best performance for many different problems and applications within deep learning.
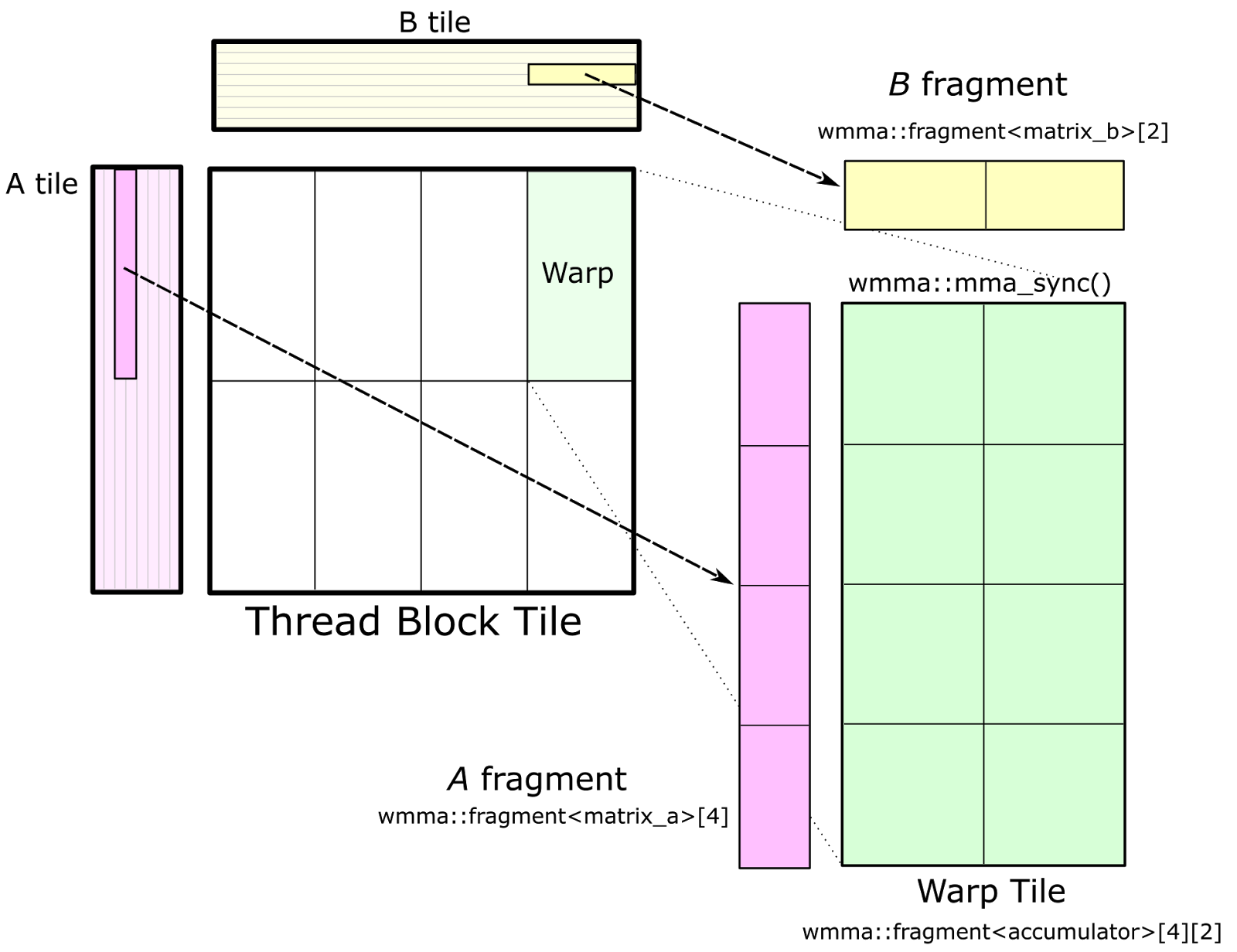
Yesterday, NVIDIA researchers introduced a preview of CUTLASS (CUDA Templates for Linear Algebra Subroutines), a collection of CUDA C++ templates and abstractions for implementing high-performance GEMM computations at all levels and scales within CUDA kernels. CUTLASS aims to give everyone the techniques and structures they need to develop new algorithms in CUDA C++ using high-performance GEMM constructs as building blocks.  The flexible and efficient application of dense linear algebra is crucial within deep learning and the broader GPU computing ecosystem.
CUTLASS algorithms and implementation are described in detail in a new NVIDIA Developer Blog post, “CUTLASS: Fast Linear Algebra in CUDA C++”

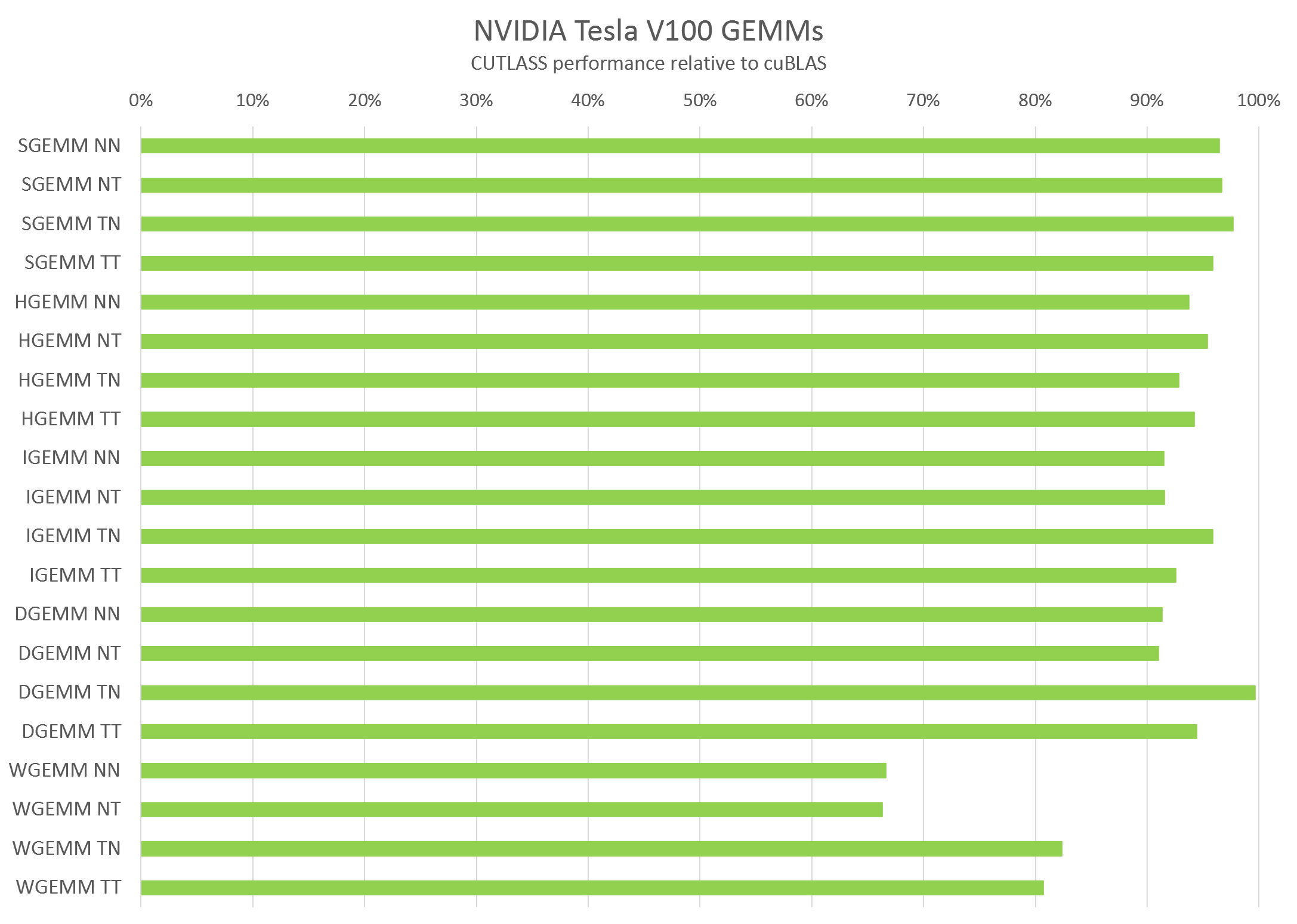
CUTLASS primitives include extensive support for mixed-precision computations, providing specialized data-movement and multiply-accumulate abstractions for handling 8-bit integer, half-precision floating point (FP16), single-precision floating point (FP32), and double-precision floating point (FP64) types.  One of the most exciting features of CUTLASS is an implementation of matrix multiplication that runs on the new Tensor Cores in the Volta architecture using the WMMA API. Tesla V100’s Tensor Cores are programmable matrix-multiply-and-accumulate units that can deliver up to 125 Tensor TFLOP/s with high efficiency.
Read more >