Enhance Text-to-Image Fine-Tuning with DRaFT+, Now Part of NVIDIA NeMo

Text-to-image diffusion models have been established as a powerful method for high-fidelity image generation based on given text. Nevertheless, diffusion models do not always grant the desired alignment between the given input text and the generated image, especially for complicated idiosyncratic prompts that are not encountered in real life. Hence, there is growing interest in efficiently fine-tuning diffusion text-to-image models to achieve prompt alignment and maximize text-to-image scoring models.

Direct reward fine-tuning (DRaFT) is a simple and effective method for fine-tuning diffusion models to maximize differentiable reward functions, as presented in Directly Fine-Tuning Diffusion Models on Differentiable Rewards.

This post explains DRaFT methods for diffusion models to better align with diverse and complex prompts. We also introduce DRaFT+, which enhances the capabilities of DRaFT methods and addresses their main shortcomings.

You can now access the DRaFT+ algorithm and sample code through the NeMo-Aligner library on GitHub. NVIDIA NeMo is an end-to-end platform for developing custom generative AI, anywhere. It includes tools for training, fine-tuning, retrieval-augmented generation, guardrailing, data curation tools, and pretrained models, offering enterprises an easy, cost-effective, and fast way to adopt generative AI. In the future, we plan to integrate the DRaFT+ algorithm into the NeMo framework container as well.

Direct reward fine-tuning (DRaFT)

The following sections explore the DraFT algorithm in detail, along with its limitations, and dive deep into how we enhanced and developed the DRaFT+ algorithm.

Given the noticeable success of reinforcement learning from human feedback (RLHF) methods in large language model (LLM) fine-tuning, the generative text-to-image community has tested similar ideas to improve image generation fidelity. With these approaches, the diffusion process is treated as a full RL trajectory and guided using a text-to-image scoring model. For more information, see DPOK: Reinforcement Learning for Fine-tuning Text-to-Image Diffusion Models and Training Diffusion Models with Reinforcement Learning.

However, these methods suffer from two drawbacks. First, reinforcement learning (RL) samples are inefficient and computationally expensive training procedures. Second, they are only successful in a narrow domain of prompts and lack generalizability across diverse prompts.

To address these issues, and as an alternative to RL, the DRaFT method suggests directly backpropagating the differentiable reward through the diffusion process. Although simpler than the RL process, this method achieves significantly better alignment between text and input prompts at a larger scale (hundreds of thousands of prompts) with computation times orders of magnitude faster.

However, the original DRaFT method is prone to reward over-optimization, mode collapse, and lack of diversity for the same prompt. To address these shortcomings, we introduce DRaFT+, which adds a regularization term to enhance generation diversity, control reward over-optimization, and prevent mode collapse.

The DRaFT method fine-tunes the Stable Diffusion v1.5 model (from High-Resolution Image Synthesis with Latent Diffusion Models) parametrized by $\theta$ against a differentiable reward model, $R$ . This objective can be formulated as follows:

${maximize}\;\mathbb{E}_{c\sim p_{c}, x_{T}\sim\mathcal{N}(\textbf{0},\textbf{1})}\big[R(x_{0}(\theta, x_{T}, c), c)\big]$

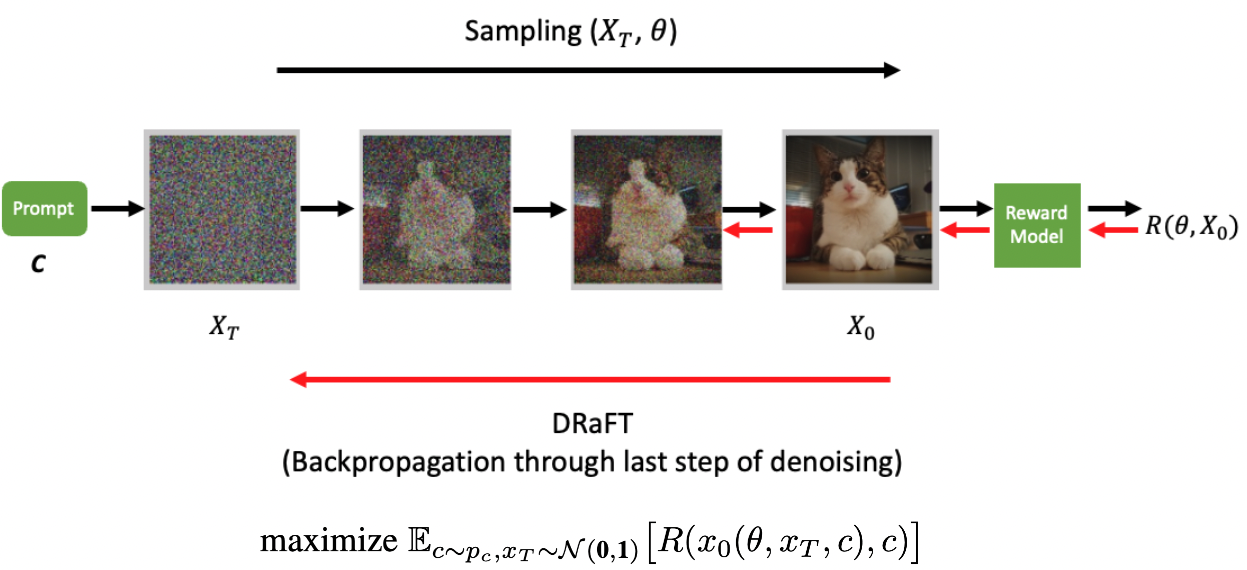
Here, $x_{0}$ is the fully denoised sample generated by the diffusion model, which is a function of the prompt conditioning, the initial pure noise, and diffusion model network parameters. Adopt the same procedure discussed in the DRaFT algorithm. That is, in the forward pass, generate a sample using the diffusion model and pass its output to the differentiable reward (reward model), R. The reward could be any differentiable objective defined on the denoised image such as image compressibility or a CLIP-based model trained on human-labeled data using a contrastive loss, to name but two.

On the backward pass, calculate the gradient of the generated reward with respect to the diffusion model weights, but only backpropagate through the reward model and only the last denoising step of the diffusion model. Surprisingly, as shown in Directly Fine-Tuning Diffusion Models on Differentiable Rewards, backpropagating more than one step into the diffusion process results in a lower reward for the algorithm.

Figure 1 illustrates the forward-backward pass using vanilla DRaFT. An initial noise sampled from a normal distribution is passed through the diffusion model to obtain a denoised image conditioned on the input text (c). The denoised image is passed to a (frozen) differentiable reward model.

A neural network model for image generation. The model takes a prompt c as input and generates an image x_0. The image is then passed through a reward model R(x_0, c) which outputs a reward. The reward is then used to update the weights of the neural network model. — *Figure 1. The fine-tuning process of image generation, in which the reward is backpropagated through the reward model and the diffusion model to update its parameter*

DRaFT+

The main drawbacks of the vanilla DRaFT algorithm are mode collapse, reward hacking, and a lack of diversity. In other words, as the diffusion model is trained against the reward model, it gradually learns to increase the reward while collapsing to the same image for different initial pure noises fed into the diffusion model $x_{T}\sim \mathcal{N}(\textbf{0},\textbf{1})$ .

The authors of DRaFT mention two attempts to address such issues: adding dropouts to the reward function and adding a term to the reward that promotes dissimilarity between image pairs in a minibatch. However, they also mention that these approaches do not completely mitigate the issue.

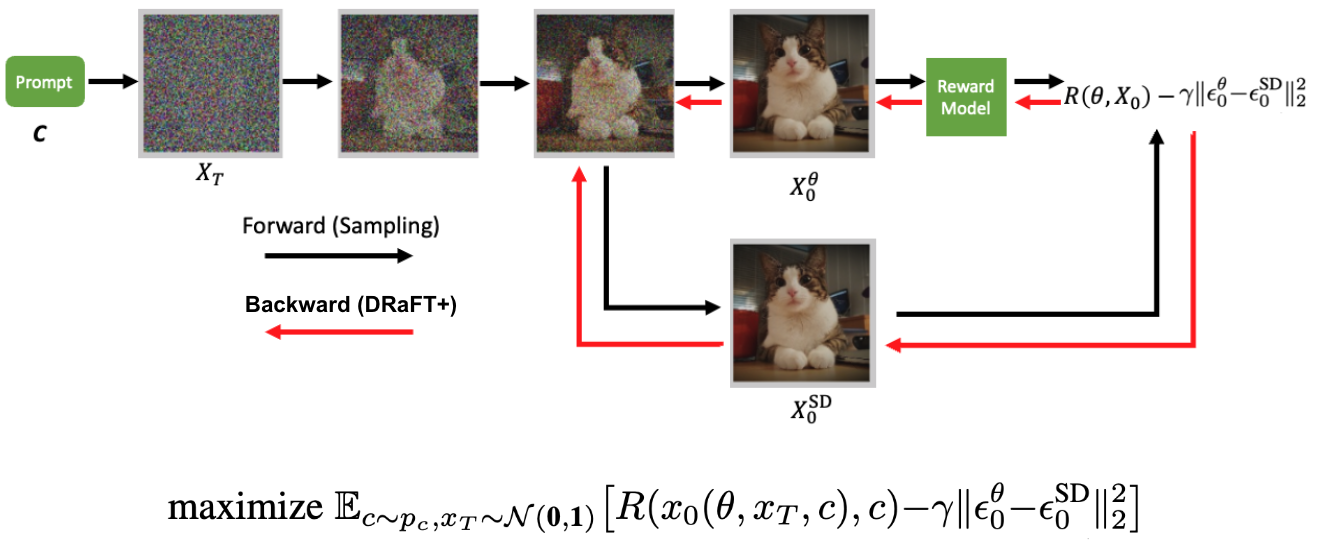
Instead, our approach uses two versions of the Stable Diffusion model, one being trained against a reward model and the other with frozen weights. Drawing from RLHF practices, we propose adding a regularization term to the training objective that penalizes dissimilarity between the frozen model and the one that is being trained.

We incorporate such a term in the objective introduced in the following training objective by adding the Kullback-Leibler (KL) divergence (here equivalent to the L2 distance) between the predicted noise Gaussians by the two models.

The image shows a neural network model for image generation. The model takes a prompt c as input and generates an image x_0. The image is then passed through a reward model R(x_0, c) which outputs a reward. The reward is then used to update the weights of the neural network model. — *Figure 2. Fine-tuning image generation using DRaFT+*

In this case, $\epsilon^{\theta}_{0}$ and $\epsilon^{\text{SD}}_{0}$ are the predicted noise at the last step of the denoising process by the model under training and that of the frozen model, and is a coefficient balancing the added term against the reward. We refer to this as the KL coefficient.

Figure 2 illustrates the forward-backward pass of the DRaFT+ algorithm. An initial noise sampled from a normal distribution is passed through the trainable diffusion model, but the last step of denoising is also done by a frozen diffusion model as well. This results in two denoised images conditioned on the input text (c). The denoised image from the trainable model is passed to the differentiable reward model. The reward minus the distance between the denoised images generated by the trainable and frozen model is backpropagated through the diffusion model to update its parameter.

Training DRaFT+ with the NeMo-Aligner library is as easy as specifying your dataset and checkpoints and running the following script:

GPFS="/path/to/nemo-aligner-repo"
TRAIN_DATA_PATH="/path/to/train_dataset.tar"
UNET_CKPT="/path/to/unet_weights.ckpt"
VAE_CKPT="/path/to/vae_weights.bin"
RM_CKPT="/path/to/reward_model.nemo"
NUM_DEVICES=#number of gpus


torchrun --nproc_per_node=${NUM_DEVICES} ${GPFS}/examples/mm/stable_diffusion/train_sd_draftp.py \
   trainer.num_nodes=1 \
   trainer.devices=${NUM_DEVICES} \
   model.micro_batch_size= \
   model.global_batch_size= \
   model.kl_coeff= \
   model.optim.lr= \
   model.unet_config.from_pretrained=${UNET_CKPT} \
   model.first_stage_config.from_pretrained=${VAE_CKPT} \
   rm.model.restore_from_path=${RM_CKPT} \
   model.data.train.webdataset.local_root_path=${TRAIN_DATA_PATH} \
   exp_manager.explicit_log_dir=/results

For more information on running scripts and setups, see the DRaFT+ User Guide.

Results of DRaFT+ training

This section presents the results of training the Stable Diffusion model with the DRaFT+ objective function. Regularization improves the diversity of the generated fine-tuned images. For this matter, we vary the coefficient of the regularization term in the objective function and plot a diversity measure versus reward.

The diversity measure we use here is the LPIPS score from The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. This essentially calculates the perceptual similarity of two given images based on the activations of two image patches from a predefined network (Alexnet), and a higher LPIPS score translates to more diverse images.

We compare the LPIPS score measure for the Stable Diffusion v1.5, vanilla DRaFT, DRaFT+ with different regularization coefficients, and DDPO. For the reward model, we use the PickScore reward model introduced in Pick-a-Pic: An Open Dataset of User Preferences for Text-to-Image Generation. Note that for the same reward, our model achieves a better diversity score.

Figure 3 shows the trade-off between diversity and reward. The graph on the left shows that lower KL results in a lower LPIPS score (less diversity and more prone to mode collapse). The graph in the middle shows that lower KL results in higher rewards. The graph on the right shows that, for the same reward, DRaFT+ achieves a better diversity score compared to vanilla DRaFT (equivalent to DRaFT+ with KL 0). In other words, in the case of a reward threshold, introducing the regularization term will lead to a model with a better diversity score while achieving that reward.

All models are trained for 200 epochs on an animals dataset. The diversity score is measured during training on a fixed dataset of 100 generated images from the same prompt, and the overall score is the average pairwise LPIPS score between the 100 images.

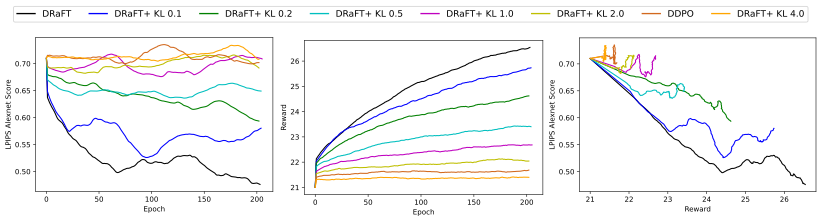
The image shows a graph comparing the performance of different detection models. The models are trained on the same dataset, and their performance is evaluated on the same set of images. The x-axis shows the number of epochs, and the y-axis shows the LPIPS Alexnet score and Reward. — *Figure 3. Examples of the trade-off between diversity and reward (higher is better for both measures)*

Figure 4 shows the generated images for the same prompt for different models after training for 200 epochs on an animal dataset. Every row in the figure contains the generated images with the same initial random seed from different variations of the model. The figure shows that for lower KL, the mode collapse is more severe while the models with higher KL stay closer to the Stable Diffusion model. Note that the addition of the regularization term is critical to prevent the mode collapse that happens in the rightmost column.

A grid of 45 images of a lion comparing different models. — *Figure 4. A comparison of the generated images for the same prompt for different models after training for 200 epochs on an animal dataset*

Finally, Figure 5 shows a few examples of a fine-tuned Stable Diffusion model with our DRaFT+ algorithm compared to the base Stable Diffusion model. Both models use the same prompts and the initial seeds for image generation. The fine-tuning is done on the Pic-a-Pic dataset prompts using the PickScore reward.

The image shows two sets of images, each set containing the same five images. The first set is labeled "Fine-tuned SD with DRaFT +" and the second set is labeled "Vanilla SD". From left to right: a cat with wings, a boat made of watermelon, a giant caterpillar riding a bike, a robot elephant, and a boy at the beach. — *Figure 5. Image examples fine-tuned with the Stable Diffusion v1.5 model with DRaFT+ and =0.25, compared to vanilla Stable Diffusion v1.5*

Summary

This post introduces the DRaFT+ algorithm for fine-tuning generative text-to-image diffusion models. This algorithm fine-tunes the diffusion process by maximizing the reward generated from a given differentiable reward model. Through a regularization term, our algorithm improves on previous methods by preventing mode collapse and enhancing diversity for image generation.

To try the DRaFT+ algorithm, visit the NeMo-Aligner library on GitHub.