Object detection and classification in imagery using deep neural networks (DNNs) and convolutional neural networks (CNNs) is a well-studied area. For some applications, these AI approaches are considered to be reliable enough to use in production with minimal intervention. Popular methods include YOLO, SSD, Faster-RCNN, MobileNet, RetinaNet, and others.

In most application contexts, imagery is collected from an egocentric viewpoint (like a mobile phone camera), with most objects being aligned vertically (a person) or horizontally (a car). This means that most of the objects in the image can be considered to be axis-aligned and can be described by four bounding box parameters: xmin, ymin, width and height.
However, there are many cases where objects or features are not aligned to the image axis. In those cases, the four parameters do not describe the object outline with high precision.

(a) Axis-aligned box 
(b) Rotated box
For example, try to describe a square that has been rotated by 45° using the four bounding box parameters. The area of the bounding box is twice that of the square that you are attempting to describe. Try the calculation yourself!
For rectangular objects, or any objects with a high aspect ratio (tall and thin, short and fat), the difference is even greater. An additional parameter is needed to reduce the difference between the area of the object and the bounding box that describes it; the object angle relative to the vertical axis, θ (theta). Now you can describe the bounding box of an object using xmin, ymin, width, height and θ.
In the real world, some objects cannot be described as a simple rectangle and require even more parameters. The addition of an angle parameter helps describe its location and outline with greater precision than an axis-aligned box.

(a) Axis-aligned bounding-box ground truth for COCO validation image 
(b) Rotated bounding-boxes detected by ODTK for the same image
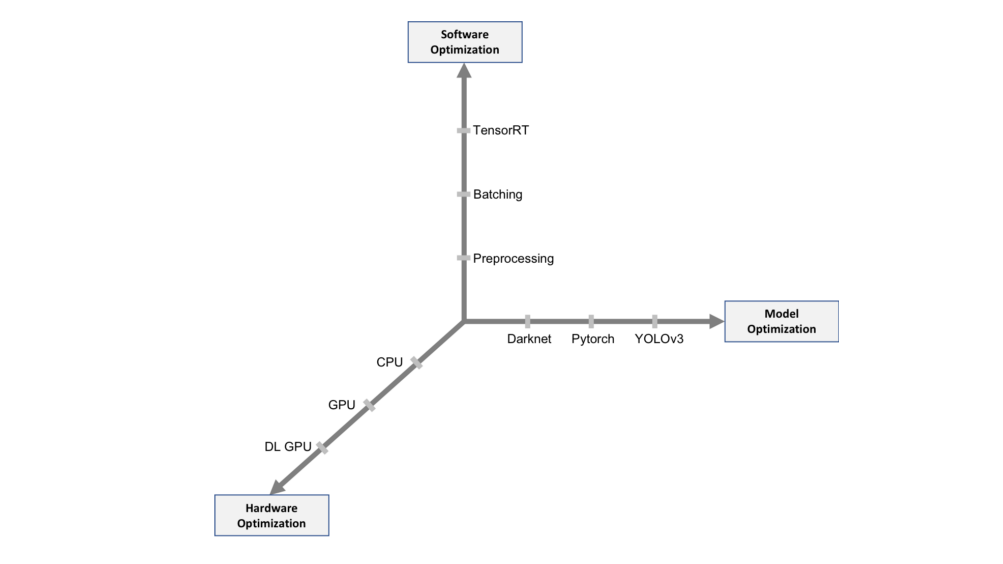
Applications that may depend on detection of rotated objects and features include remote sensing (Figure 1), text detection “in the wild,” medical physics, and industrial inspection. When you are using axis-aligned bounding boxes for training a model background, features are included with each rotated object, reducing the model’s ability to differentiate the objects of interest from the background imagery. In addition, if objects are in close proximity, cars in a parking lot for example, background and nearby objects are also included in the object instance.
The result is a detector which may over– or undercount objects where there are clusters of the same or similar classes. This is obviously suboptimal for applications that rely on accurate values. Rotated bounding boxes can mitigate these problems and provide a higher precision and recall. For example, the axis-aligned box around the person in Figure 3 contains a lot of sky and some of the motorbike. The rotated box contains less sky and almost no motorbike.
Rotated object detection models and methods
Common DNN methods to detect rotated objects can be grouped into two areas:
- Calculating rotated bounding boxes from segmentation masks
- Directly inferring the rotated bounding box
For the first method, segmentation masks are usually calculated using Mask-RCNN, a network based on Faster-RCNN, with an additional segmentation head alongside the classification and axis-aligned bounding box detection heads. Mask-RCNN, like Faster-RCNN, is a two-stage detector that infers region proposals then refined into detections.
Although this method can produce high-precision inferences for axis-aligned objects, the performance (images processed per second) of such two-stage methods is relatively low. In addition, calculating a rotated bounding box using an inferred segmentation mask, usually with post processing and standard packages such as OpenCV, can produce inaccurate and spurious results.
The second method, directly inferring rotated boxes, is much more attractive. Unlike the segmentation mask method, post processing, which adds inefficiencies and commonly reduces precision, is not required. Plus, the majority of the methods that directly infer rotated boxes are single-shot detectors, not slower multi-stage detectors like Faster-RCNN.
There are few academic papers on this topic, and even fewer publicly available repositories. To infer boxes in a single pass, many techniques rely on comparing ground truth annotations to anchor boxes, sometimes known as prior boxes. For axis-aligned detectors, anchor box sizes, aspect ratios, and scales are defined by the user before training occurs.
During training, if the calculated intersection over union (IoU) value between an anchor box and a ground truth box is above 0.5, then the anchor box parameters are regressed to minimize the difference when compared to the ground truth bounding box (Δxmin, Δymin, Δwidth, Δheight). For axis-aligned bounding boxes, the IoU calculation is very simple to perform and can be accelerated using NVIDIA GPUs in an end-to-end manner. The following PyTorch example shows the IoU calculation between axis-aligned boxes and anchors:
inter = torch.prod((xy2 - xy1 + 1).clamp(0), 2) boxes_area = torch.prod(boxes[:, 2:] - boxes[:, :2] + 1, 1) anchors_area = torch.prod(anchors[:, 2:] - anchors[:, :2] + 1, 1) overlap = inter / (anchors_area[:, None] + boxes_area - inter)
In this code example:
boxesare the ground truth annotations.anchorsare the anchor boxesxy2andxy1are the furthest and nearest box corners from the origin respectively between boxes and anchorsinteris the intersection betweenboxesandanchorsboxes_areaandanchors_areaare the areas of the ground truth and anchor boxes, respectivelyoverlapis the IoU
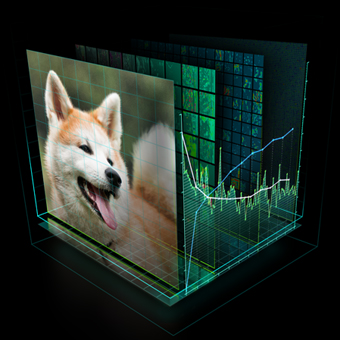
For rotated boxes, the situation is different. Firstly, you specify one or more values for an extra parameter, angle, which increases the total number of anchor boxes by a factor equal to the number of angles defined. Figure 4 shows example axis-aligned bounding anchor boxes (blue), for a single location in image feature space, with three scales and three aspect ratios. Rotated anchor boxes (red and blue) are shown using the same scales and aspect ratios for three rotation angles: -π/6, 0 and π/6 radians. Secondly, and most importantly, the IoU calculation cannot be performed in a simple manner similar to the axis-aligned boxes as shown earlier.
Calculating IoU between rotated boxes
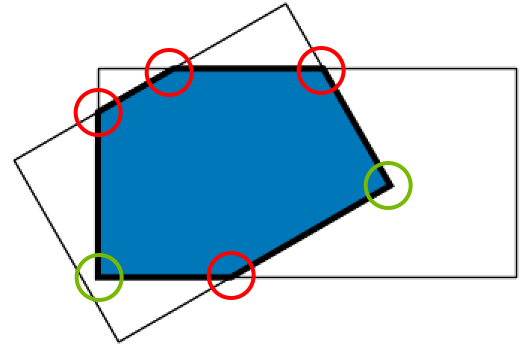
Figure 5 shows an example of how rotated box intersections can be much more complex than axis-aligned box intersections. When overlapping two boxes, you construct a new polygon (not necessarily four-sided), which is described by red and green vertices. Red vertices denote where edges of the two boxes intersect, while the green vertices are contained within the two boxes being compared. You must be able to calculate these points for all box comparisons, and then perform the IoU calculation.
Most papers and repositories rely on rasterizing the boxes (for example, creating an image or mask) to calculate this new polygon and then compute the IoU. This is an inefficient and inaccurate method as the space that the boxes occupy must be discretized for all comparisons. Use precise analytical solutions to maximize efficiency and accuracy.
To solve this problem, turn to geometry, particularly the method of sequential cutting expertly described in the book Computational Geometry: Algorithms and Applications. Sequential cutting is a recursive method that defines an initial polygon using one box under comparison. For each edge, it then calculates whether there are any intersections with edges from the second box under comparison. If so, these vertices are kept and new edges are formed, which are then compared again to the box under comparison until there are no edges remaining. The pseudocode is as follows:
Intersection of two rotated boxes / polygons (p1, p2): 1. Initialize the box_intersection, setting it as the vertices of p1. 2. For each edge (specified by the line equation ax + by + c = 0) of p2, find line intersection with box intersection using homogeneous coordinates where; intersectionx = (p1.b*p2.c - p1.c*p2.b) / w intersectiony = (p1.c*p2.a - p1.a*p2.c) / w where; w = p1.a*p2.b - p1.b*p2.a 2a. If intersection occurs on the edge, add it to temp_intersection. 2b. If intersection occurs within the boundary of two edge calculations, add it to temp_intersection. 3. Set box_intersection = temp_intersection. 4. Repeat from 2. until no more edges.
If a polygon with more than two edges exists when comparing the two boxes, you can now calculate the IoU; otherwise, the IoU is zero. Again, turn to geometry for exact calculations where the area of an irregular polygon is given by the following formula:
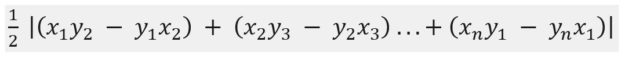
IoU is then calculated by dividing the polygonal area as calculated earlier by the union of the areas of the boxes and anchors.
This recursive method is more complex when compared to its axis-aligned counterpart. However, it is less computationally demanding and less cumbersome than rasterizing boxes and anchors.
The IoU calculation must occur for every image as it is fed forward through the DNN. During training the IoU is used to measure loss; during inference IoU is needed for non-maximum suppression (NMS). Therefore, the function must be as fast as possible.
This is achieved by parallelizing each comparison over multiple GPU threads inside a CUDA kernel using grid-striding. For more information about examples of CUDA and grid-striding, see An Even Easier Introduction to CUDA.
Instead of sequentially calculating all ground truth box to anchor box comparisons (many 100ks to millions of calculations per image batch) grid-striding allows you to perform these calculations in parallel in a flexible manner on the GPU device.
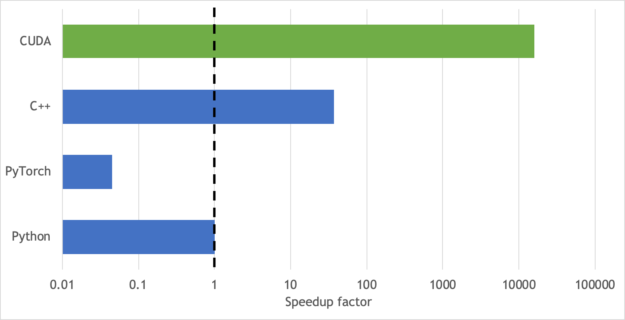
Figure 6 presents a plot of the speedup provided when implementing a CUDA kernel (green bar) compared to performing sequential calculations on CPUs (blue bars). The CUDA kernel provides >10k speedup over Python, >100k speedup over PyTorch, and a >500 speedup over C++. This chart does not consider the data transfer times between the GPU to CPU and back if rotated IoU calculations were to be performed off the GPU device during model training. Keeping all the data and calculations on the GPU throughout training and inference further increases the difference between GPU and CPU performance than shown in Figure 6.
Now that IoU is calculated, you can minimize (Δxmin, Δymin, Δwidth, Δheight, Δθ) if absolute angle is not required. If absolute angle is required and the orientation needs to be known (text box orientation, vehicle direction / bearing, and so on) and this information is consistent within the ground truth, you can minimize (Δxmin, Δymin, Δwidth, Δheight, Δsin(θ), Δcos(θ)), which captures absolute angle differences by projecting θ onto a unit circle.
All the features (axis-aligned and rotated bounding box detection) are available in the NVIDIA Object Detection Toolkit (ODTK).
Using the ODTK
NVIDIA has a rich suite of tools for accelerating the training and inference of object detection models. The open-source ODTK is an example of how to use all of these tools together. The demonstration detection pipeline uses RetinaNet as a good example of a modern object detector.
The ODTK demonstrates how to integrate five NVIDIA tools:
- Mixed precision training. We keep a master copy of the network weights at FP32, but we calculate the update each batch at FP16. This gives a 3x speedup while training. We implement automatic mixed precision (AMP) using the NVIDIA APEX library.
- NVIDIA Data Loading Library (DALI) moves pre-processing (image resize and normalization) to the GPU. This can increase both training and inference speeds between 1.2 and 1.5x, depending which backbone you choose.
- NVIDIA TensorRT creates highly optimized inference engines, at FP32, FP16, and INT8 precision. These engines can give significant speedups (such as 5x) during inference. ODTK can also generate ONNX files, providing greater framework flexibility.
- NVIDIA DeepStream SDK is the NVIDIA solution for intelligent video analytics (IVA). It is highly effective because DeepStream keeps the video data on the GPU for the entire pipeline. NVIDIA provides a parser, so that the ODTK inference engine (produced using TensorRT) can be used in the DeepStream pipeline.
- NVIDIA Triton Inference Server is another way of serving TensorRT models. ODTK PyTorch, ONNX, and TensorRT models can be registered by Triton Inference Server, which can be requested by the Triton client. This method may be more suitable if you are using still images instead of video streams.
Preparing your data
ODTK uses the COCO object detection format, but we modify the bounding boxes to also include a theta parameter. Bounding boxes are first constructed using the [xmin, ymin, width, height] parameters (Figure 7, left). Then, the box is rotated anticlockwise by theta radians, in this case -0.209. It doesn’t matter if the rotated box includes the area outside of the picture frame.
Many datasets (for example, COCO and ISPRS) come with segmentation masks. These masks can be converted into rotated bounding boxes by using a geometry package.
Use the shapely minimum_rotated_rectangle function to create the rotated rectangles, and feed the four corners into function 1 to produce the bounding box values. calc_bearing is a simple function that finds theta by using arctan. You must wrap function 1 to ensure that w and h are positive, and that theta is either in the range -pi/2 to pi/2 or -pi to pi.
def _corners2rotatedbbox(corners): centre = np.mean(np.array(corners), 0) theta = calc_bearing(corners[0], corners[1]) rotation = np.array([[np.cos(theta), -np.sin(theta)], [np.sin(theta), np.cos(theta)]]) out_points = np.matmul(corners - centre, rotation) + centre x, y = list(out_points[0,:]) w, h = list(out_points[2, :] - out_points[0, :]) return [x, y, w, h, theta]
Train, infer, and export an ODTK model
ODTK is located in the latest NVIDIA NGC PyTorch container. This ensures that the correct version of PyTorch and other prerequisites are installed. For more information, see NVIDIA Object Detection Toolkit (ODTK) on GitHub.
git clone https://github.com/nvidia/retinanet-examples docker build -t odtk:latest retinanet-examples/ docker run --gpus all --rm --ipc=host -it -v/your/data/dir:/data odtk:latest
Now, train ODTK for rotated detections. For this post, we used the ResNet50PFN backbone. The following command produces a validation score every 7000 iterations.
odtk train model.pth --backbone ResNet50FPN \ --images /data/train/ --annotations /data/train.json \ --val-images /data/val --val-annotations /data/val.json --rotated-bbox
You can infer your model using PyTorch:
odtk infer model.pth --images /data/test --output detections.json
However, you get faster inference performance if you first export to TensorRT, here at FP16, but INT8 precision is also available.
odtk export model.pth engine.plan
You can infer using the odtk infer command, Triton Server, or by writing a C++ inference app.
| Backbone | Inference latency INT8 on T4 | Inference latency FP16 on V100 |
| ResNet18FPN | 18 ms; 56 FPS | 14 ms; 71 FPS |
| MobileNetV2FPN | 18 ms; 56 FPS | 14 ms; 74 FPS |
| ResNet34FPN | 20 ms; 50 FPS | 16 ms; 64 FPS |
| ResNet50FPN | 22 ms; 45 FPS | 18 ms; 56 FPS |
| ResNet101FPN | 27 ms; 37 FPS | 22 ms; 46 FPS |
| ResNet152FPN | 33 ms; 31 FPS | 26 ms; 38 FPS |
Comparison examples

Figure 8 shows examples of axis-aligned and rotated-box models trained on the ISPRS Potsdam dataset, fine-tuned from an axis-aligned model pretrained on the COCO dataset with a ResNet18 backbone. Both models are trained until convergence (90k iterations) on the same training and validation dataset split.
It is evident from the example inference image that the rotated model matches the ground truth better than the axis-aligned model. Cases appear where there are multiple detections per vehicle when using an axis-aligned model, but this is not the case for the rotated-box model.
The rotated model achieves a higher average IoU when compared to the axis-aligned model: 0.60 versus 0.29. Due to the lower IoU obtained by the axis-aligned model, the standard COCO average precision calculation values at an IoU ≥ 0.5 are different between the models: 0.86 and 0.01. You must use a fairer metric for this comparison, one that captures how well inferred detections match the ground truth boxes.
For this post, we used the instance-level semantic labeling metric as defined in the Cityscapes dataset challenge. Precision and recall are calculated at a per-class and per-pixel level. When using these metrics, the rotated model achieves a precision and recall of 0.77 and 0.76, respectively, while the axis-aligned model achieves a precision and recall of 0.37 and 0.55, respectively. Rotated detections clearly match the ground truth better than the axis-aligned model.
| Precision | Recall | F1 Score | |
| Axis-aligned model | 0.37 | 0.55 | 0.44 |
| Rotated model | 0.77 | 0.76 | 0.76 |
Summary
Try using ODTK to detect rotated objects in your own dataset. You will find it straightforward to train, validate, operationalize, and serve your model with maximum efficiency on your GPU resources. Stay tuned for high performance, end-to-end mask training and inference, polygon detection, and efficient multi-object tracking integration.
The authors wish to thank their colleagues Matt Nicely for his CUDA support and Yash Vardhan for his help in maintaining and extending the ODTK repo.