Leyuan Wang, a Ph.D. student in the UC Davis Department of Computer Science, presented one of only two “Distinguished Papers” of the 51 accepted at Euro-Par 2015. Euro-Par is a European conference devoted to all aspects of parallel and distributed processing held August 24-28 at Austria’s Vienna University of Technology.
Leyuan Wang, a Ph.D. student in the UC Davis Department of Computer Science, presented one of only two “Distinguished Papers” of the 51 accepted at Euro-Par 2015. Euro-Par is a European conference devoted to all aspects of parallel and distributed processing held August 24-28 at Austria’s Vienna University of Technology.
Leyuan’s paper Fast Parallel Suffix Array on the GPU, co-authored by her advisor John Owens and Sean Baxter, a research scientist at New York’s DE Shaw Research, details their efforts to implement a linear-time suffix array construction algorithm on NVIDIA GPUs, resulting in algorithmic improvements and significant speedups over the existing state of the art.
Wang completed her master’s degree in electrical and computer engineering at UC Davis in October 2014, after having earned her undergraduate degree in electronics science and technology at China’s Zhejiang University.
Brad: Can you talk a bit about your current research?
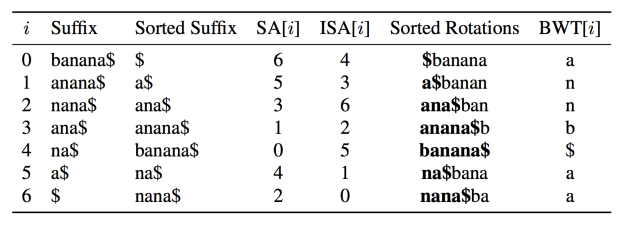
Leyuan Wang: I work on high-performance string processing and graph processing algorithms, mostly in string and graph queries. My current research focus is on GPGPU (general-purpose computing on graphics processing units) and the benchmark I care about most is speed. I’ve been working on designing and improving parallel suffix array construction algorithms (SACAs) and incorporating the implementations in a Burrows-Wheeler transform-based lossless data compression (bzip2) and a parallel FM index for pattern searching. The suffix array (SA) of a string is the sorted set of all suffixes of the string. The inverse suffix array (ISA) is also the lexicographic ranks of suffixes.
The Burrows-Wheeler transform (BWT) of a string is generated by lexicographically sorting the cyclic shift of the string to form a string matrix and taking the last column of the matrix. The BWT groups repeated characters together by permuting the string; it is also reversible, which means the original string can be recovered. These two characteristics make BWT a popular choice for a compression pipeline stage (for instance, bzip2). It is directly related to the suffix array: the sorted rows in the matrix are essentially the sorted suffixes of the string and the first column of the matrix reflects a suffix array. Table 1 shows an example of the SA, ISA and BWT of the input string “banana$”
The suffix array data structure is a building block in a spectrum of applications, including data compression, bioinformatics, text indexing, etc. I’ve studied the taxonomy of all classes of SACAs and compared them in order to find the best candidate for the GPU. I revisited the previous conclusion that skew SACAs are best suited on the GPU by demonstrating that prefix-doubling SACAs are actually better both in theoretical analysis and experimental benchmarks. Our hybrid skew/prefix-doubling suffix array implementation (with our amazing research collaborator Sean Baxter, formerly of NVIDIA Research) using a Tesla K20 achieves a 7.9x speedup against the previous state-of-the-art skew implementation. Our optimized skew SACA implementation has been added as a primitive to CUDPP 2.2 (CUDA Data Parallel Primitives Library) and incorporated into the BWT and bzip2 data compression application, resulting in great speedups compared with bzip2 in CUDPP 2.1. Figure 1 shows pseudocode for our two approaches.

For graph queries, I’ve been working on subgraph matching, which is an NP-complete problem that is used to find a small query graph in a large data graph. It has wide use in deep-workload graph applications such as fraud detection. Triangle counting is a simple version of subgraph matching since a triangle is a simple subgraph of an entire data graph. Since triangles are the basic unit of work in graph analytics, the ability to count them quickly is pretty important. I use the Gunrock programming model, which is a high-performance GPU-accelerated graph processing library created in our research group. The functionality of subgraph matching is similar to what commercial companies like Neo4j perform with their Cypher query language, but hopefully with much better performance. What we focus on is large-scale graph analytics which can hit the sweet spot of today’s ambitious graph users and deep graph workloads (high-diameter graphs where the paths in the queries are as long as hundreds to thousands of traversals) beyond interpersonal connections towards deeper things that can be touched in the network.
B: Why did you start using NVIDIA GPUs?
LW: I started learning parallel programming on the GPU when I took the Udacity course “Introduction to Parallel Programming using CUDA” and a graduate course called “Computer Graphics” at UC Davis two years ago. After that, I started to use NVIDIA GPUs and found myself very interested and passionate in programming with CUDA. And since then, GPUs have been playing a key role in my research life.
B: What is your GPU Computing experience and how have GPUs impacted your research?
LW: My first GPU computing project implemented the connected components algorithm on the GPU using CUDA, which was my course project for “Computer Graphics”, where I got a speedup of 5x compared with the original method on the CPU. I used an NVIDIA Geforce 540M card and CUDA 5.0 when I ran the experiments. My masters thesis was on optimizing suffix array construction algorithms (SACAs) on the GPU, where we achieve a speedup of 1.45x over the previous state-of-the-art skew implementation by Deo and Keely. The optimized skew implementation has been added as a parallel primitive to the latest version of CUDA Data Parallel Primitives Library (CUDPP). We also revisited Deo and Keely’s conclusion that skew is best suited for GPUs among all SACAs and implement a high-performance skew/prefix-doubling hybrid with a speedup of up to 7.9x over their work and along with an analytic comparison, we conclude that prefix-doubling is actually better suited for the GPU. Both of the implementations used NVIDIA Tesla K20c GPUs running CUDA 6.0.
GPU computing has revolutionized my research. With the continued increase of GPU memory capacity and bandwidth, I can try to implement more and more complicated algorithms.
B: Can you share some performance results?
LW: The following is a detailed experimental evaluation of our implementations of suffix array algorithms. Our experimental setup has an Intel Core i7-3770K 3.5 GHz 4-core CPU and an NVIDIA Tesla K20c GPU.
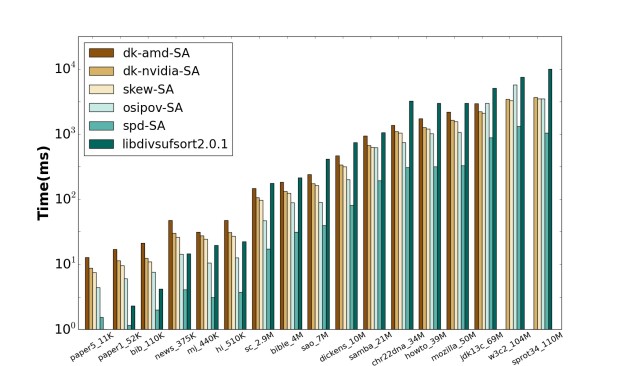
For a more thorough comparison, we re-implementedDeo and Keely’s method using a current state-of-the-art radix sort primitive from Duane Merrill’s CUB library and a merge primitive from Sean Baxter’s Modern GPU library. For convenience, we call Deo and Keely’s OpenCL parallel skew implementation on an AMD GPU dk-amd-SA, our CUDA implementation of Deo and Keely’s approach dk-nvidia-SA, Osipov’s parallel prefix-doubling implementation osipov-SA, our parallel skew implementation skew-SA, and our parallel hybrid skew/prefix-doubling implementation spd-SA.
For evaluation, we use the same input datasets as Deo and Keely along with two larger datasets. The input strings range in size from 10KB to 110MB and are collected from a wide range of Corpus datasets. We compare the four GPU implementation results against Mori’s highly tuned, OpenMP-assisted current fastest CPU implementation libdivsufsort 2.0.1 based on induced copying on a 4-core CPU, using its own internal runtime measurement, which excludes disk access time.
Figures 2 and 3 summarize our performance results and we make the following observations:
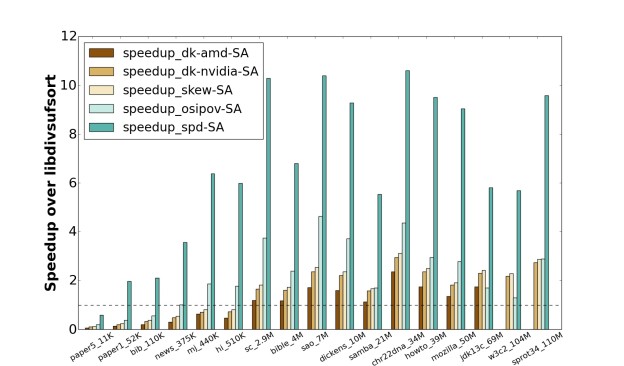
- On datasets of sufficient size (on the order of 1MB for the skew implementations, smaller for spd-SA), all four GPU implementations are faster than the CPU baseline. Roughly speaking, the skew implementations are twice as fast as the CPU version, osipov-SA has a 4x speedup, and spd-SA‘s speedup ranges from 6x to 11x.
- Macroscopically, the fluctuations in the speedups of spd-SA and osipov-SA for the same datasets suggest that the behavior of spd-SA is similar to that of osipov-SA, and our skew-SA is similar to dk-amd-SA and dk-nvidia-SA.
- Our hybrid skew/prefix-doubling spd-SA is 2.3x to 4.4x (for w3c2_104M dataset) faster than Osipov’s plain prefix-doubling implementation osipov-SA.
- Our skew-SA is consistently 1.45x faster than dk-amd-SA and 1.1x faster than dk-nvidia-SA.
- Both prefix-doubling based GPU implementations outperform the three skew based methods on most datasets.
B: How are you using GPUs?
LW: My research is all about GPU computing, especially using CUDA. I like tackling parallel algorithmic problems. With the help of GPUs, our performance optimizations of some complex problems achieve amazing speedups. I’m interested in researching the structure of parallelism and locality in irregular algorithms, and GPUs help me understand them quickly. I also like to use GPUs in course projects in computer graphics and machine learning areas.
B: What NVIDIA technologies are you using (GPUs, math libraries, etc)?
LW: In our group, we have servers with NVIDIA Tesla K40 cards which we use for development and simulation. I really like the fact that GPUs are getting larger memories so that I can run my tests on larger datasets without having to use multiple GPUs.
For both the robustness and parallelism of my implementations of different algorithms, I’ve been trying to use as many parallel primitives from CUDA libraries as possible. The open-source CUDA libraries I’ve been using include CUDPP (CUDA Data Parallel Primitives), Modern GPU, and Gunrock (a high-performance graph processing library). And I myself have also been contributing parallel primitives to CUDPP and Gunrock.
B: Can you share some visual results?
LW: Sure. When we run experiments on our two different classes of suffix array implementations, we find that the datasets with the highest speedups on GPUs are those with a non-uniform prefix distribution (e.g., chr22dna in Fig. 3, which contains DNA sequences of only 4 different characters), whereas more uniformly distributed prefixes yield smaller speedups. The peaks of the speedup happen because the GPU implementations (especially our hybrid skew/prefix-doubling) are faster on non-uniform prefixes. For skew, a more uniform dataset results in more iterations in the recursive step, and thus takes longer time. For prefix-doubling, uniform datasets give us fewer segments for separation and thus result in lower parallelism.
We take a closer look at two datasets for our skew-SA and hybrid skew/prefix-doubling spd-SA implementations. The first is a scalability test on increasing amounts of text data from the English Wikipedia dump “enwik8“, shown in Figure 4. In general, the larger the dataset, the higher the throughput; it takes an input size of many millions of characters for both approaches to reach the throughput asymptote. At 10 MB, skew-SA has a 2x speedup and spd-SA a 9x speedup over the fastest CPU implementation libdivsufsort.
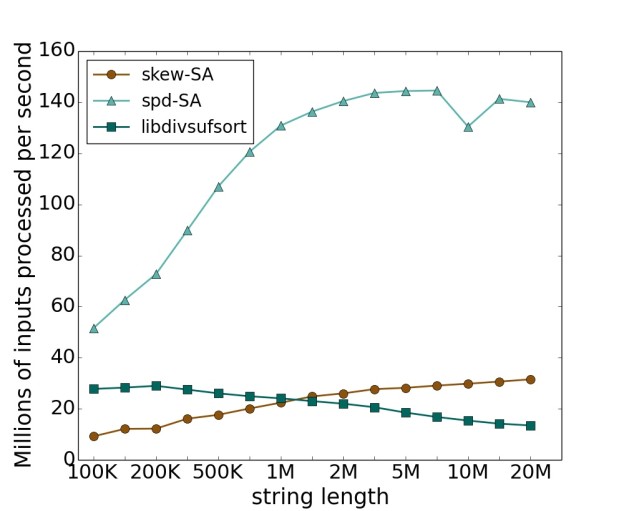
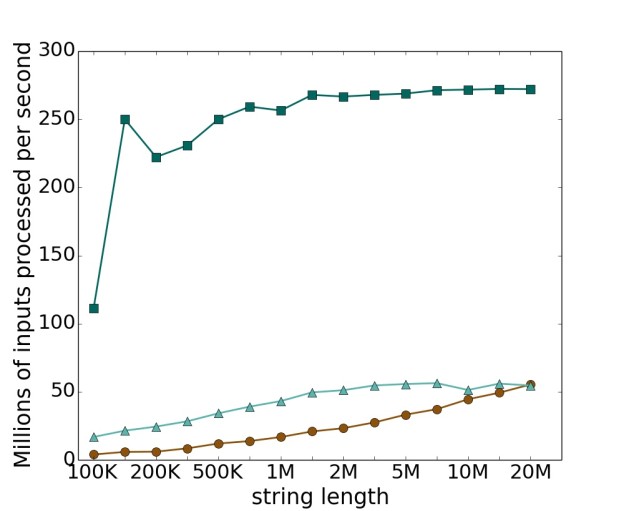
The second is an artificial dataset composed of only the repeated single character ‘A’. This is a pathologically bad case for prefix-doubling because (except for suffixes near the end of the string) every input position has an identical prefix on every iteration until the last one, so spd-SA cannot divide the prefixes into multiple segments—they all land in the same segment. Moreover, because those prefixes in that segment are lexicographically identical, they have worst-case sorting behavior. Skew’s performance is much more predictable; although skew must recurse all the way to the base case and cannot finish early, it is not pathologically bad as with prefix-doubling. Nonetheless, except for very large inputs, spd-SA’s performance still exceeds skew-SA’s. Induced copying would be much better suited for this dataset. For a 10 MB all-‘A’ input, libdivsufsort completes in 40 ms, compared with 224 ms for skew-SA and 196 ms for spd-SA. The result is shown in Fig. 5.
B: What challenges have you overcome in your work?
LW: Efficient GPU programs should have enough work per kernel to keep all hardware cores busy (load-balancing); aim to access memory in large contiguous chunks to maximize achieved memory bandwidth (coalescing); and minimize communication between CPU and GPU. Designing a parallel algorithm that achieves all of these goals is a significant challenge. To address this challenge, we prioritize using high-performance parallel algorithmic GPU building blocks when applicable.
Another challenge for us is performance optimization for solving many small problems in parallel especially when we tried to implement the prefix-doubling SACA. Since we already have suffixes with the same h-prefix in the same buckets, we need to sort within each bucket while keeping the order of the buckets. It’s hard to parallelize because there are a large number of buckets each of which has a different size unknown beforehand. There’s no efficient sorting method that can sort both small and large problems simultaneously. Fortunately Sean Baxter’s segmented sort primitive provides a solution to this kind of problem (Figure 6 shows a running example of the segmented sort method). Efforts to develop building blocks to solve similar GPU computing difficulties are greatly helpful.

B: What’s next? What’s your vision?
LW: GPUs will be more compatible, with much faster communication with CPUs and within GPUs, and have larger memory. And with the speed requirements of embedded systems in people’s everyday lives, embedded GPU computing will also become more and more common. In general, GPUs will play a more and more important role in a system shoulder-to-shoulder with CPUs.
B: What impact do you think your research will have on this scientific domain? Why?
LW: Suffix array data structures have been widely used in bioinformatic applications such as genetic pattern searching, and speed, with the explosion in data sizes, becomes a more and more important factor. My SA approach, as a building block for many string processing applications, has great potential for next-generation suffix array construction and bioinformatics applications.
B: Where do you obtain technical information related to NVIDIA GPUs and CUDA?
LW: Both from my research group (“Owens Group” at UC Davis) especially from my advisor John Owens and from GTC conferences.