Accelerating Real-Time Financial Decisions with Quantitative Portfolio Optimization

Financial portfolio optimization is a difficult yet essential task that has been consistently challenged by a trade-off between computational speed and model complexity. Since the introduction of Markowitz Portfolio Theory 70 years ago, robust analysis beyond basic mean-variance—such as large-scale simulations, multistep optimizations, or richer risk measures—was too slow for dynamic decision-making, blocking rapid iteration.

The Quantitative Portfolio Optimization developer example, introduced in this post, is designed to eliminate this trade-off. With high-performance hardware and parallel algorithms, it transforms optimization from a slow, batch process into a fast, iterative workflow.

The pipeline enables scalable strategy backtesting and interactive analysis. NVIDIA cuOpt open source solvers enable efficient solutions to scenario-based Mean-CVaR portfolio optimization problems. These consistently outperform state-of-the-art open source CPU-based solvers, with up to 160x speedups in large-scale problems.

Quantitative Portfolio Optimization also takes advantage of the broader CUDA ecosystem. The CUDA-X Data Science library accelerates pre-optimization data preprocessing and scenario generation, delivering speedups of up to 100x when learning and sampling from return distributions.

Mathematical foundations of portfolio optimization

An optimal portfolio should maximize expected return while minimizing risk. The classical risk-return trade-off formulation introduced by Markowitz can be written as:

$\textit{maximize}_{w}$	$\mu^\top w - \frac{\lambda}{2}\,\text{risk}$
$\textit{subject\; to}$	$\sum_i w_i = 1$

where $\mu$ is the expected returns of the assets and $w$ is the wealth allocation vector.

Traditionally, variance of portfolio returns is used as the measure of risk. Here, Conditional Value-at-Risk (CVaR) was chosen as an alternative risk measure because it provides a more robust assessment of potential tail losses. It also allows for a data-driven approach to portfolio optimization without making assumptions on the underlying returns distribution. CVaR measures the average worst-case loss of a return distribution.

Formally, for a loss random variable $L$ :

$CVaR = {E}[L| L \geq VaR_\alpha (L)]$

where $VaR_\alpha(L) = \inf\{l: P(L \leq l) \geq \alpha \}$ is the $\alpha$ -quantile of the loss distribution.

Figure 1 shows the probability distribution of daily log returns. The 95% VaR, marked by the red dashed line at -4.35%, indicates that the portfolio loss is not expected to exceed 4.35% with 95% confidence. The 95% CVaR, marked by the blue dashed line at -5.58%, represents the average loss on the worst 5% of scenarios (the shaded tail region).

A chart illustrating VaR and CVaR. The chart displays a histogram of log returns with an overlaid normal distribution curve. The x-axis represents Log Return and the y-axis represents Probability Density. A vertical red dashed line indicates the 95% VaR at a log return of -4.35%. A vertical blue dashed line indicates the 95% CVaR at -5.58%. The tail of the distribution to the left of the VaR line is shaded, representing the worst 5% of returns. — *Figure 1. Probability distribution of daily log returns for 95% VaR and CVaR*

CVaR is a more appropriate risk measure for portfolios that may contain assets with asymmetric return distribution and has replaced VaR in Basel III market-risk rules. Mathematically, CVaR is a coherent risk measure—satisfying subadditivity, translation invariance, positive homogeneity, and monotonicity—which aligns with the diversification principles.

Moreover, it has a computationally tractable transformation as a scenario-based optimization: for confidence level $\alpha$ , the CVaR of portfolio $w$ can be written in abstract form as:

$CVaR({w}) = \min_t\left\{t + \frac{1}{1-\alpha}\sum_{\omega \in \Omega}p(\omega)\max \{\text{loss}({w},\omega) - t, 0\}\right\}$

where $\Omega$ is the probability space of returns scenarios and $p(\omega)$ is the probability of a particular scenario $w$ .

Intuitively, this expression represents the portfolio’s average loss below the $\alpha$ -quantile of all return scenarios. This scenario-based formulation makes CVaR more robust, regardless of whether the asset returns distribution is Gaussian or not. When linear loss is used, $\text{loss}(w,\omega) = -R(\omega){w}$ with $R$ as the return scenarios matrix of size (num_scenarios, num_assets), the minimization of the CVaR can be transformed into a linear program by replacing the $\max\{\cdot, 0\}$ non-negative operator with an auxiliary variable $u$ :

$\textit{minimize}$	$t \;+\; \frac{1}{1-\alpha}\, p^\top u$
$\textit{subject\; to}$	$u + t \ge -R^\top w,$
	$u \ge 0.$

Integrating this into a risk-return tradeoff formulation results in the following the mathematical optimization problem of maximizing the CVaR-risk-adjusted return:

$\textit{maximize}$	$\mu^\top w - \lambda_{\text{risk}}\!\left(t + \frac{1}{1-\alpha} p^\top u\right)$
$\textit{subject\; to}$	$u + t \ge -R^\top w,\; u \ge 0 \; (CVaR)$
	$\sum_i w_i + c = 1 \; (self\text{-}financing)$
	$w_i^{min} \le w_i \le w_i^{max},\; \forall i \; (concentration)$
	$c^{min} \le c \le c^{max} \; (cash)$
	$L = \lVert w \rVert_1 \le L^{limit} \; (leverage)$
	$T = \lVert w - w_{pre} \rVert_1 \le T^{limit} \; (turnover)$

Additional constraints were added to model real-world trading limitations including the concentration limits on investment budgets ( $1^\top w + c = 1$ ), single assets ( $w_i^{min}, w_i^{max}$ ), amount invested in risk-free assets ( $c^{min}, c^{max}$ ), leverage constraints ( $L^{\text{limit}}$ ), and turnover from an existing portfolio/benchmark ( $T^{\text{limit}}$ ).

Shifting portfolio optimization from CPU to GPU

This mean-CVaR problem is characterized by a linear objective and linear constraints, with complexity scaling linearly with the number of return scenarios and tradable assets. Tradable assets are often thousands in practical investment settings, and a sophisticated scenario generation engine can easily produce hundreds of thousands of different return scenarios.

As the problem size grows, high-performance solvers become increasingly important for efficient optimization. This is addressed by leveraging the cuOpt Linear Program (LP) solver, which implements the Primal-Dual Hybrid Gradient for Linear Programming (PDLP) algorithm on GPUs. For large-scale problems (often with over 10K variables and 10K constraints), the full power of cuOpt is unlocked, drastically reducing the solve time.

Accelerated workflow example

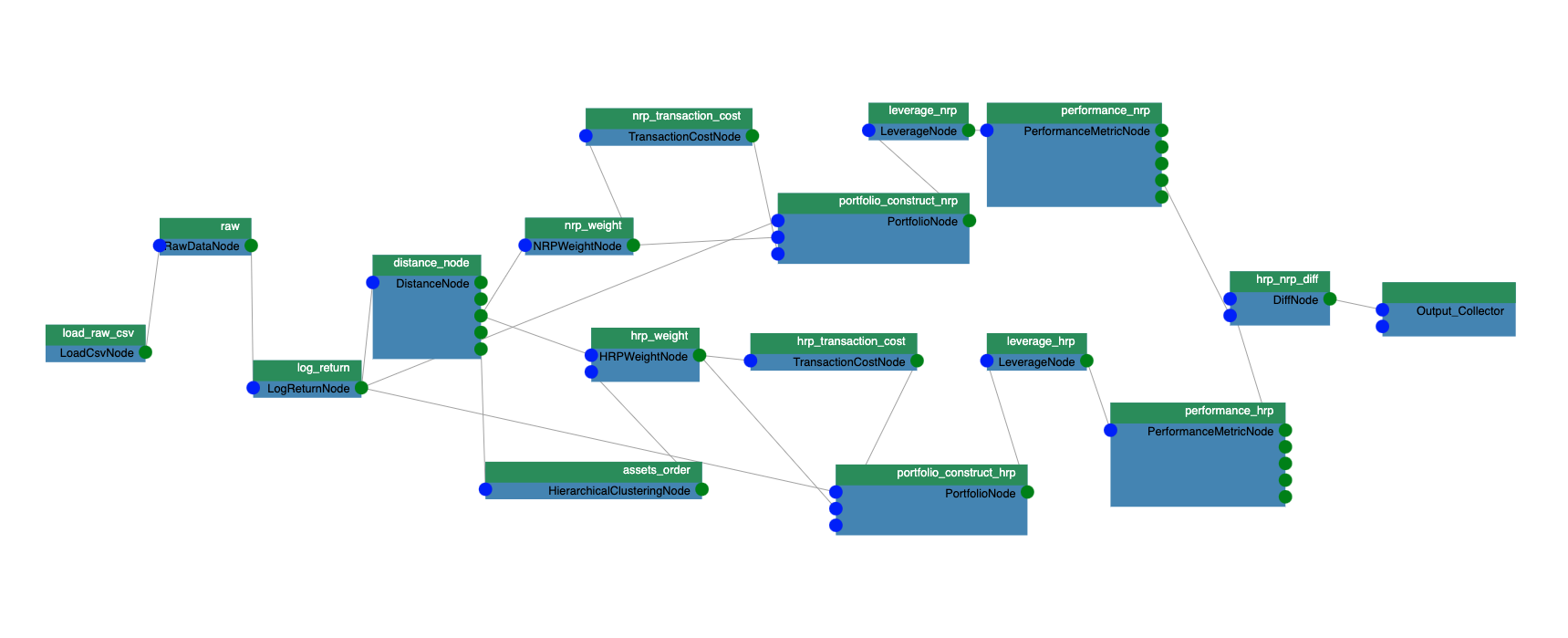
This section showcases the Quantitative Portfolio Optimization developer example on a 397-stock subset of the S&P 500. The aim is to build a long-short portfolio that maximizes risk-adjusted returns while meeting custom trading constraints. As shown in Figure 2, the workflow unfolds in four steps:

Data preparation: Estimate returns and generate CVaR scenarios from historical prices
Optimization setup: Construct the Mean–CVaR problem using the preprocessed data
Solve: Run the cuOpt solver to obtain portfolio weights
Backtest: Visualize the optimized portfolio and compute performance metrics

The architecture diagram of the Quantitative Portfolio Optimization developer example. Input data is processed into scenarios using CUDA-X DS. The cuOpt GPU optimizer then solves for an optimal allocation using methods like Mean-CVaR. Finally, the strategy is simulated, and results from backtesting and portfolio managers drive a continuous re-optimization cycle. — *Figure 2. Architecture of the Quantitative Portfolio Optimization developer example*

Step 1: Data preparation

Assume the return distribution is stationary over the optimization period and use historical returns to approximate future ones. If this assumption does not hold, you could instead optimize over a forecasted return distribution that accounts for potential shifts in market conditions.

As an example of the former approach, load closing prices from 2022-01-01 to 2024-07-01 and compute daily log‐returns. Next, fit a Kernel Density Estimator (KDE) to those returns and simulate 20K return scenarios.

...
# Define the settings for returns computation
returns_compute_settings = {'return_type': 'LOG', 'freq': 1}

# Compute returns from price data
returns_dict = utils.calculate_returns(
    data_path,
    regime_dict,
    returns_compute_settings
)

...
# Define the settings for scenario generation
scenario_generation_settings = {
'num_scen': 20000, # Number of return scenarios to simulate 
 	'fit_type': 'kde', 
      'kde_settings': {'bandwidth': 0.01, 
                       'kernel': 'gaussian', 
                       'device': 'GPU'
                      },
                      'verbose': False
}

# Generate return scenarios from KDE
sp500_returns_dict = cvar_utils.generate_cvar_data(
    returns_dict,
    scenario_generation_settings
)

Notably, using GPU acceleration through cuML for KDE fitting and sampling yields significant acceleration compared to CPU, especially as dataset sizes and the number of scenarios to sample increase. Figure 3 shows a direct comparison of cuML GPU speedups, represented by CPU time divided by GPU time, as compute demands rise.

A bar chart comparing the performance of CPU and GPU with cuML for Kernel Density Estimation (KDE) fitting and sampling. The x-axis represents asset datasets of different sizes, ‘dow30’, ‘Global Titans’, and ‘SP500.’ For each dataset, there are three colored bars representing a different number of scenarios to sample “20K”, “50K”, and “100K”. The y-axis represents the GPU speed up factor, and the CPU baseline is represented by a horizontal dashed line at y=1. The GPU shows significant speed-ups over the CPU, and the performance improves as the dataset size and number of scenarios to sample increase. — *Figure 3. CPU versus GPU with cuML performance on KDE fitting and sampling*

GPU: NVIDIA H200; CPU: Intel Xeon Platinum 8480+ processor

Step 2: Optimization setup

The following parameters are used to set up a Mean-CVaR portfolio optimization problem:

# Define CVaR optimization parameters for the S&P 500 example
sp500_cvar_params = CvarParameters(
    #Asset weight allocation bounds
    w_min={'NVDA':0.1, 'others': -0.3}, w_max={'NVDA':0.6, 'others':0.4},                
    c_min=0.0, c_max=0.2,         # Cash holdings bounds
    L_tar=1.6,                    # Leverage 
    T_tar=None,                   # Turnover (None for this example)
    cvar_limit=None,              # Hard limit on CVaR (None = unconstrained)
    cardinality = None,           # Max number of assets allowed in the portfolio
    risk_aversion=1.0,            # Risk aversion level
    confidence=0.95,              # CVaR confidence level 
)

All the optimization parameters can be customized. For example, you can adjust per-asset concentration limits by specifying the ticker and the desired weights constraints in a dictionary. You can also adjust the risk aversion level (higher risk averseness generally leads to more diversification). Finally, you can restrict the number of assets in the optimal portfolio by adding a cardinality constraint.

Then, use the returns data from Step 1 and the problem parameters to formulate the problem:

# Instantiate CVaR optimization problem for the S&P 500 example
sp500_cvar_problem = cvar_optimizer.CVaR(
    returns_dict=sp500_returns_dict,
    cvar_params=sp500_cvar_params
)

Step 3: Solve

Next, call the cuOpt LP solver and obtain the optimized portfolio. You can also provide customized configurations to the cuOpt LP solver, including solver mode, accuracy, and so on. For more details, see the cuOpt documentation.

For this example, use the cuOpt PDLP default tolerance of 1e-4, and by default, cuOpt runs PDLP, barrier, and dual simplex methods in parallel. It returns the solution from whichever method completes first.

# GPU solver settings
gpu_solver_settings = {"solver": cp.CUOPT, 
                       "verbose": False, 
                       "solver_method": "Concurrent", 
                       "time_limit":15, 
                       "optimality": 1e-4
                       }

# Solve on GPU
gpu_results, gpu_portfolio = cvar_problem.solve_optimization_problem(solver_settings=gpu_solver_settings)

The optimized portfolio—under the specified constraints and risk‐aversion level—chooses long positions in 12 stocks and short positions in 2 stocks out of the 397 stocks. Also verify from the results that the optimized portfolio satisfies all the constraints.

============================================================
CVaR OPTIMIZATION RESULTS
============================================================
PROBLEM CONFIGURATION
------------------------------
Solver:              CUOPT
Regime:              recent
Time Period:         2021-01-01 to 2024-01-01
Scenarios:           20,000
Assets:              397
Confidence Level:    95.0%

PERFORMANCE METRICS
------------------------------
Expected Return:     0.002537 (0.2537%)
CVaR (95%):          0.025700 (2.5700%)
Objective Value:     -0.001396

SOLVING PERFORMANCE
------------------------------
Setup Time:          0.4921 seconds
Solve Time:          0.3685 seconds

OPTIMAL PORTFOLIO ALLOCATION
------------------------------

PORTFOLIO: CUOPT_OPTIMAL
----------------------------------------
Period: 2021-01-01 to 2024-01-01

LONG POSITIONS (12 assets)
-------------------------
LLY         0.326 ( 32.64%)
NVDA        0.151 ( 15.11%)
MCK         0.136 ( 13.60%)
IT          0.101 ( 10.13%)
IRM         0.098 (  9.84%)
JBL         0.097 (  9.71%)
PWR         0.083 (  8.25%)
STLD        0.070 (  6.96%)
COP         0.056 (  5.64%)
FICO        0.043 (  4.28%)
MRO         0.021 (  2.07%)
NUE         0.018 (  1.78%)
Total Long    1.200 (120.01%)

SHORT POSITIONS (2 assets)
--------------------------
MTCH       -0.248 (-24.85%)
ILMN       -0.148 (-14.82%)
Total Short   -0.397 (-39.67%)

CASH & SUMMARY
--------------------
Cash        0.200 ( 20.00%)
Residual    0.000 (  0.01%)

Net Equity         0.803 ( 80.33%)
Total Portfolio    1.003 (100.35%)
Gross Exposure     1.597 (159.68%)
----------------------------------------
============================================================

The developer example streamlines the solver calls, making it very easy to use any solver. With zero code changes, you can call a different solver by changing the solver settings. For example, to compare performance against a CPU solver, simply declare a new solver:

solver_settings = {'solver': "CUSTOM_SOLVER", 'verbose': False} 

#solve the optimization problem using an open-source CPU solver
cpu_results, cpu_portfolio = cvar_problem.solve_optimization_problem(solver_settings)

Table 1 compares the performance of the cuOpt solver against a state-of-the-art open source CPU solver, solving problems with 20,796 variables and 20,796 constraints with approximately 8 million nonzero entries in the constraint matrix. Set both solvers with an optimality tolerance of 1e-4, and for cuOpt, select the PDLP solve method.

The cuOpt solver was run on the NVIDIA H200 GPU, and the CPU solver was using the Intel Xeon Platinum 8480+ processor. The cuOpt LP solver consistently outperforms the CPU solver, reducing solve time from minutes to the subsecond range.

	CPU Solver	cuOpt GPU Solver	Speedup versus CPU
Regime	Solver time (s)	Solver time (s)	X
Pre-crisis (‘2005-01-01’, ‘2007-10-01’)	70.36	0.53	131.7
Crisis (‘2007-10-01’, ‘2009-04-01’)	42.19	0.92	45.8
Post-crisis (‘2009-06-30’, ‘2014-06-30’)	75.50	0.45	167.4
Oil price crash (‘2014-06-01’, ‘2016-03-01’)	53.43	0.51	105.6
FAANG surge (‘2015-01-01’, ‘2021-01-01’)	49.89	0.73	68.0
Covid (‘2020-01-01’, ‘2023-01-01’)	57.43	0.66	86.5
Recent (‘2022-01-01’, ‘2024-07-01’)	56.32	0.56	99.5

Table 1. Solve time comparison between a state-of-the-art open source CPU solver and cuOpt GPU solver over problems with data from different regimes, with GPU speedups (rightmost column)

20K scenario; 397 assets; GPU: NVIDIA H200; CPU: Intel Xeon Platinum 8480+

The efficient frontier is a set of optimal investment portfolios that offer the highest expected return for a given level of risk or the lowest risk for a specified expected return. To compute the efficient frontier, it’s necessary to solve a sequence of optimization problems for different risk aversion levels.

For example, in Figure 4, an efficient frontier of 50 optimal portfolios with different risk-aversion levels is generated. The video in 4x speed shows that the cuOpt GPU solver enables generating the efficient frontier much faster than using a CPU solver in real time.

A video in 4x speed comparing the speed of the cuOpt GPU solver and a state-of-the-art open source CPU solver in generating an efficient frontier with 50 portfolios. The video demonstrates that the cuOpt GPU solver is significantly faster, completing the task in significantly less time. — *Figure 4.* Using the cuOpt GPU solver (left), you can generate the efficient frontier much faster than using a CPU solver (right) in real time (4x video speed)

Step 4: Backtest

Finally, you can backtest the optimized portfolio and evaluate some key metrics such as cumulative returns, Sharpe Ratio, and max drawdown. In the following example, the backtester is initiated and compared to the performance of the optimized portfolio against an equal-weight portfolio (allocate equal weights in every available asset):

from src import backtest

# Create backtester and run backtest
backtester = backtest.portfolio_backtester(gpu_portfolio, test_returns_dict, risk_free, test_method, benchmark_portfolios = None)

backtest_result,_ = backtester.backtest_against_benchmarks(plot_returns=True, cut_off_date=cut_off_date)

During the backtest period, with the dashed line indicating the start of out-of-sample testing, the optimized portfolio consistently outperformed the equal-weight benchmark and generated substantially greater value.

On the left, a horizontal bar plot showing the optimized portfolio allocation, with x-axis representing asset weights, and y-axis representing tickers of selected assets. On the left, a chart showing the cumulative returns of a GPU-optimized portfolio compared to an equal-weight benchmark portfolio over time. The x-axis represents the date, from 2022-07-01 to 2024-05-01. The y-axis represents the cumulative returns. A dashed vertical line indicates the start of out-of-sample testing on 2024-01-01. The optimized portfolio's cumulative returns are consistently higher than the equal-weight portfolio's returns. — *Figure 5. The optimized portfolio allocation (left) and backtest results (right)*

Dynamic rebalancing

Dynamic rebalancing is critical because a once‑optimal portfolio drifts as market conditions evolve—the estimated returns distribution is nonstationary. Rather than holding a static allocation, trigger‑based rebalancing (for example, portfolio value moves or weight deviations) adjusts exposures to protect against downside risk and keep the portfolio aligned with the risk budget in real time.

This requires repeated re‑optimization. Exploring different rebalancing strategies often means hundreds of iterations, so optimization time scales with the number of repetitions. A fast, accurate solver is essential: the Quantitative Portfolio Optimization developer example can complete these tasks in minutes instead of hours or days on a traditional CPU solver.

For example, compare two strategies—value‑percentage change and allocation drift—against buy‑and‑hold from 2022‑07‑01 to 2024‑05‑01. The portfolio is backtested every three months (63 trading days), and if the monitored metric exceeds a user‑defined threshold, re‑optimization is triggered.

In Figure 6, rebalancing occurs when the portfolio value experiences a cumulative 0.5% drop since the last positive change. Over the period, the rule triggered four times, producing a 15.6% total return and outperforming buy‑and‑hold.

A line chart showing the cumulative returns of a percentage change rebalancing strategy versus a buy-and-hold strategy over time. The x-axis represents the date, and the y-axis represents the cumulative returns. The percentage-change rebalancing strategy consistently outperforms the buy-and-hold strategy, showing higher cumulative returns. Vertical dashed lines indicate the points in time when rebalancing events were triggered. — *Figure 6. Portfolio performance of percentage change rebalancing strategy*

A video in 4x speed comparing the speed of the cuOpt open source GPU-accelerated solver and a state-of-the-art open source CPU solver in testing percentage-change rebalancing strategy. The video demonstrates that the cuOpt GPU solver is significantly faster, completing the task in significantly less time. — *Figure 7.* Using the cuOpt GPU solver (left), you can test a percentage-change rebalancing strategy much faster than using a CPU solver (right) in real time (4x video speed)

Figure 8 shows testing a different strategy, where rebalancing is triggered when the current portfolio composition shifts away from the original allocation. As prices move, weights drift and the portfolio may no longer meet required constraints, justifying a re‑optimization with new market data. Again, the rebalancing strategy stays on top of the market and yields a positive return.

A line chart showing the cumulative returns of a portfolio with a drift-from-optimal rebalancing strategy versus a buy-and-hold strategy over time. The x-axis represents the date, and the y-axis represents the cumulative returns. The drift-from-optimal rebalancing strategy consistently outperforms the buy-and-hold strategy, showing higher cumulative returns. Vertical dashed lines indicate the points in time when rebalancing events were triggered. — *Figure 8. Portfolio performance of drift-from-optimal rebalancing strategy*

A video in 4x speed comparing the speed of the cuOpt GPU solver and a state-of-the-art open source CPU solver in testing the drift-from-optimal rebalancing strategy. The video demonstrates that the cuOpt GPU solver is significantly faster, completing the task in significantly less time. — *Figure 9.* Using the cuOpt GPU solver (left), you can test a drift-from-optimal rebalancing strategy much faster than using a CPU solver (right) in real time (4x video speed)

Portfolio optimization is a repeated core task rather than a one‑time effort—the acceleration cuOpt delivers for a single optimization problem will be magnified in active trading environments. There are more sophisticated strategies with more hyperparameters, and searching for the optimal strategy will require repeating the above process countless times. In other words, these example strategies highlight GPU acceleration and are not optimized for deployment. To find the optimal strategies, many more iterations of optimization are needed.

Get started with portfolio optimization

Optimization workflows are only as fast as their slowest step. By moving data preparation, scenario generation, and solving to GPUs, the Quantitative Portfolio Optimization developer example eliminates common bottlenecks and reduces solve times from minutes and hours to seconds. The payoff grows in repeated workflows—reallocation, sweeping parameter spaces, stress tests, and backtests—where hundreds of re-optimizations are routine.

With cuOpt for LP solving and CUDA-X DS for preprocessing and simulation, you can iterate more frequently, test richer constraints, and respond to market changes in near real-time. The result is faster time‑to‑insight, better use of CVaR‑based models at scale, and a practical path to dynamic rebalancing. The Quantitative Portfolio Optimization developer example makes large‑scale, risk‑aware portfolio optimization an interactive capability rather than a batch chore.

Transform portfolio optimization with GPU acceleration and run complex risk models and allocations in real time. Achieve faster insights, scalable performance, and smarter, data-driven investment strategies.

Visit build.nvidia.com to deploy the notebook in a GPU-accelerated environment with either NVIDIA Brev or your own cloud infrastructure using the Quantitative Portfolio Optimization notebook on GitHub.

Accelerating Real-Time Financial Decisions with Quantitative Portfolio Optimization

Mathematical foundations of portfolio optimization

Shifting portfolio optimization from CPU to GPU

Accelerated workflow example

Step 1: Data preparation

Step 2: Optimization setup

Step 3: Solve

Step 4: Backtest

Dynamic rebalancing

Get started with portfolio optimization

Tags

About the Authors

Accelerating Real-Time Financial Decisions with Quantitative Portfolio Optimization

Mathematical foundations of portfolio optimization

Shifting portfolio optimization from CPU to GPU

Accelerated workflow example

Step 1: Data preparation

Step 2: Optimization setup

Step 3: Solve

Step 4: Backtest

Dynamic rebalancing

Get started with portfolio optimization

Tags

About the Authors

Comments

Related posts

GPU-Accelerate Algorithmic Trading Simulations by over 100x with Numba

Writer Releases Domain-Specific LLMs for Healthcare and Finance

Profit and Loss Modeling on GPUs with ISO C++ Language Parallelism

Free Digital Webinar Series: How to Get Started with AI Inference

NVIDIA H100 System for HPC and Generative AI Sets Record for Financial Risk Calculations