DirectX 光线跟踪中自相交伪影的求解

光线和路径跟踪算法通过从摄影机或光源开始并将光线与场景几何体相交来构建光路。当对象被击中时，会在这些曲面上生成新的二次光线以继续路径。

理论上，这些二次光线不会再次与同一三角形相交，因为相交算法排除了距离为零的相交。然而，在实践中，实际实现中使用的有限浮点精度往往会导致假阳性结果，称为自交叉（图 2）。这会产生伪影，例如阴影痤疮，其中三角形有时会不正确地阴影自己（图 1）。

通过使用同一基元的标识符显式地将其从交集中排除，可以避免自交集。在 DirectX 光线跟踪（DXR）中，这种自相交检查将在任何命中着色器中实现。然而，强制任何命中 所有三角形命中的调用都会带来显著的性能损失。此外，该方法不处理针对相邻（近）共面三角形的误报。

解决该问题的最广泛的方案是使用各种启发式方法来沿着光线方向或法线偏移光线。然而，这些方法不足以处理各种常见的制作内容，甚至可能需要在每个场景的基础上手动调整参数，特别是在具有大量平移、缩放或剪切实例化几何体的场景中。有关详细信息，请参阅 Ray Tracing Gems: High-Quality and Real-Time Rendering with DXR and Other APIs.

或者，可以在运行时对数值不精确性的来源进行数值限制，从而在交叉测试中给出稳健的误差区间。然而，这会带来相当大的性能开销，并且需要对射线/三角形相交例程的底层实现进行源访问，这在 DXR 等硬件加速的 API 中是不可能的。

这篇文章描述了一种强大的偏移方法，用于从 DXR 中的三角形派生的二次光线。该方法基于对数值不精确性来源的彻底数值分析。它涉及计算二次光线的生成点，避免自相交。该方法不需要修改遍历和光线/三角形相交例程，因此可以与 DXR 等闭源和硬件加速的光线跟踪 API 一起使用。最后，该方法不依赖于使用任意命中着色器的自相交拒绝，并且每个着色点有固定的开销。

方法概述

二次光线的生成点与入射光线三角形上的命中点重合。目标是计算一个尽可能靠近三角形平面中的命中点的生成点，同时仍然避免自相交。离三角形太近可能会导致自相交伪影，但离得太远可能会将生成点推过附近的几何体，从而导致漏光伪影。

图 2 显示了二次射线的数值误差来源。在用户着色器中，对象空间的命中点被重建并变换到世界空间中。在 DXR 光线遍历过程中，世界空间光线将变换回对象空间并与三角形相交。

这些运算中的每一个都会累积数值误差，可能导致自相交。该方法在每次操作时计算三角形上以预期光线原点（图 2 中的红点）为中心的最小不确定性区间。近似射线原点（图 2 中的黑点）位于该不确定性区间内。光线原点沿三角形法线偏移超过最终不确定性区间，以防止自相交。

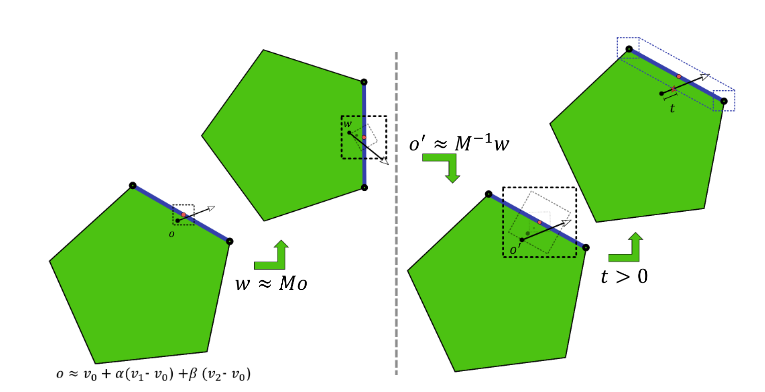
命中点

首先在对象空间中重建命中点和几何三角形法线（清单 1）。

precise float3 edge1 = v1 - v0;
precise float3 edge2 = v2 - v0;

// interpolate triangle using barycentrics
// add in base vertex last to reduce object-space error 
precise float3 objPosition = v0 + mad(barys.x, edge1, mul(barys.y, edge2));
float3 objNormal = cross(edge1, edge2);

通过对三角形顶点进行插值来计算命中点v0，v1,和v2使用 2D 重心命中坐标重锤。虽然可以使用两个融合的乘加运算来计算插值的命中点，但是添加基顶点v0最后减小了基顶点上的最大舍入误差，该误差在实际计算中占主导地位。

使用准确的关键字，强制编译器完全按照指定执行计算。不需要强制精确计算法线和误差边界。舍入误差对这些量的影响微乎其微，可以安全地忽略自交。

接下来，将对象空间的位置转换为世界空间（清单 2）。

const float3x4 o2w = ObjectToWorld3x4(); 

// transform object-space position
// add in translation last to reduce world-space error
precise float3 wldPosition; 
wldPosition.x = o2w._m03 + 
	mad(o2w._m00, objPosition.x, 
mad(o2w._m01, objPosition.y, 
mul(o2w._m02, objPosition.z ))); 
wldPosition.y = o2w._m13 + 
mad(o2w._m10, objPosition.x, 
mad(o2w._m11, objPosition.y, 
mul(o2w._m12, objPosition.z )));
wldPosition.z = o2w._m23 + 
mad(o2w._m20, objPosition.x , 
mad(o2w._m21, objPosition.y , 
mul(o2w._m22, objPosition.z )));

不使用 HLSL 矩阵 mul 本质，而是写出变换。这样可以确保平移部分最后添加了转换的。这再次减少了平移上的舍入误差，而在实践中，舍入误差往往主导该计算中的误差。

最后，将对象空间法线转换为世界空间，并对其进行规范化（清单 3）。

const float3x4 w2o = WorldToObject3x4();

// transform normal to world-space using 
// inverse transpose matrix
float3 wldNormal = mul(transpose((float3x3)w2o), objNormal); 

// normalize world-space normal
const float wldScale = rsqrt(dot(wldNormal, wldNormal)); 
wldNormal = mul(wldScale, wldNormal);

// flip towards incoming ray 
if(dot(WorldRayDirection(), wldNormal) > 0) 
wldNormal = -wldNormal;

若要支持具有不均匀缩放或剪切的变换，法线将使用反向转置变换进行变换。在变换之前不需要规范化对象空间法线。无论如何，有必要在世界空间中再次正常化。由于稍后需要再次使用世界法线的反向长度来适当缩放误差边界，因此手动进行归一化，而不是使用 HLSL规范化固有的

错误界限

使用近似的世界空间位置和三角形法线，继续计算计算位置的误差边界，边界为最大有限精度舍入误差。有必要考虑清单 1 和 2 中计算中的舍入误差。

还需要考虑遍历过程中可能出现的舍入错误（图 2）。在遍历过程中，DXR 将应用世界到对象的变换并执行射线三角形相交测试。这两者都是以有限精度执行的，因此会引入舍入误差。

首先计算一个组合的对象空间误差边界，同时考虑清单 1 中的舍入误差和 DXR 射线三角形相交测试引起的舍入误差（清单 4）。

const float c0 = 5.9604644775390625E-8f;
const float c1 = 1.788139769587360206060111522674560546875E-7f; 
 
// compute twice the maximum extent of the triangle 
const float3 extent3 = abs(edge1) + abs(edge2) + 
   abs(abs(edge1) - abs(edge2)); 
const float extent = max(max(extent3.x, extent3.y), extent3.z); 
 
// bound object-space error due to reconstruction and intersection 
float3 objErr = mad(c0, abs(v0), mul(c1, extent));

请注意，三角形交点上的误差受沿三维的最大三角形范围的限制。这一界限的严格证明超出了本文的范围。为了提供直观的对正，在执行相交测试之前，常见的光线三角形相交算法将三角形重定向到“光线空间”（通过减去光线原点）。在自相交的上下文中，光线原点位于三角形上。因此，该光线空间中剩余三角形顶点的大小由三角形沿每个维度的范围限定。

此外，这些相交算法将三角形投影到 2D 平面中。此投影会导致沿一个维度的误差扩散到其他维度。因此，取沿所有维度的最大范围，而不是单独处理沿维度的误差。射线三角形相交测试的精确边界将是硬件特定的。常数c1针对 NVIDIA RTX 硬件进行了调整，但可能需要在不同平台上进行一些调整。

自定义相交基本体的错误边界取决于其相交着色器的实现细节。想要深入了解有限精度舍入误差的分析，请参阅 Advanced Linear Algebra: Foundations to Frontiers。

接下来，计算由于命中点从对象空间到世界空间的转换而导致的世界空间误差界限（清单 5）。

// bound world-space error due to object-to-world transform 
const float c2 = 1.19209317972490680404007434844970703125E-7f; 
float3 wldErr = mad(c1, mul(abs((float3x3)o2w), abs(objPosition)), 		
     mul(c2, abs(transpose(o2w[3]))));

这就留下了 DXR 在光线遍历过程中执行的从世界到对象变换的舍入错误（清单 6）。

// bound object-space error due to world-to-object transform 
objErr = mad(c2, mul(abs(w2o), float4(abs(wldPosition), 1)), objErr);

与射线三角形相交测试一样，世界到对象变换中的舍入误差取决于硬件。常数c2是保守的，并且应该足以用于实现向量矩阵乘法的各种方式。

世界到对象变换矩阵及其逆的有限精度表示不能保证精确匹配。在分析中，表示中的错误可以归因于其中之一。由于对象到世界的转换是在用户代码中执行的，因此错误最好归因于对象到世界转换矩阵，从而实现更严格的边界。

抵消

上一节解释了如何计算二次光线构造和遍历的舍入误差的边界。这些边界在近似的、有限精度的射线原点周围产生一个区间。预期的、全精度的“真实”射线原点保证位于该区间的某个位置。

真正的三角形通过真正的光线原点，所以三角形也通过这个区间。图 3 显示了如何沿三角形法线偏移近似原点，以确保其位于真实三角形之上，从而防止自相交。

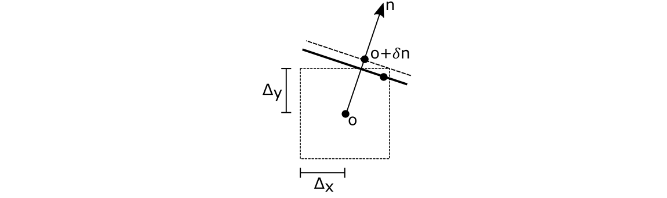
将误差界∆投影到法线 n 上，以获得沿法线的偏移δ

法线上的舍入误差与误差边界和偏移本身计算上的舍入错误具有相似的大小。这些都是微不足道的，在实践中可以忽略不计。将对象和世界空间偏移合并为沿世界空间法线的单个世界空间偏移（清单 7）。

// compute world-space self-intersection avoidance offset 
float objOffset = dot(objErr, abs(objNormal)); 
float wldOffset = dot(wldErr, abs(wldNormal)); 

wldOffset = mad(wldScale, objOffset, wldOffset);

使用已规范化的世界空间法线来自清单 3。世界空间偏移简化为.对象空间偏移沿着对象空间法线需要转化为世界空间。

但是，请注意，变换后的对象空间偏移不一定平行于世界空间法线。若要获得沿世界空间法线的单个组合偏移，请将变换后的对象空间偏移投影到世界空间法线上，如.使用这简化为：

最后，使用计算出的偏移量沿着三角形法线扰动命中点（清单 8）。

// offset along the normal on either side. 
precise float3 wldFront = mad( wldOffset, wldNormal, wldPosition);
precise float3 wldBack  = mad(-wldOffset, wldNormal, wldPosition);

这就产生了前面和后面的产卵点，它们不会发生自交叉。导出的误差边界（以及偏移）既不取决于入射光线方向，也不取决于出射二次光线方向。因此，可以对源自该命中点的所有次级光线重复使用相同的生成点。所有反射光线都应该使用前生成点，而透射光线应该使用后生成点。

方向的对象到世界和世界到对象变换也会导致光线方向上的舍入误差。在极端的掠角下，这些舍入误差可能会导致它翻转，将其定向回三角形。这篇文章中的抵消方法并不能防止这种舍入误差。通常建议滤掉极端角度的二次光线。

或者，可以在光线方向变换上导出类似的误差边界。然后，沿三角形法线偏移光线方向（对于光线原点）可以保证其侧性。然而，由于常见 BRDF 模型的反射率分布在掠入射角处趋于零，因此在许多应用中可以安全地忽略这个问题。

对象空间

如清单 4 所示，偏移量在对象空间中的三角形范围和三角形底顶点的大小中线性增长。对于小三角形，底顶点的舍入误差将主导对象空间误差（图 2）。因此，可以通过在对象空间中重新定位几何体，使其围绕对象空间原点居中，以最小化到原点的距离，来减少对象空间误差。对于具有超大三角形的几何体（如地平面），可能值得对几何体进行镶嵌，并进一步减少三角形范围中的舍入误差。

摄像头空间

如清单 5 和 6 所示，偏移量的大小将随着世界空间位置的大小线性增长。比例常数c2约为 1 ulps。远处的实例化几何体来自世界空间中场景原点的最大舍入误差为，或每 4 公里偏移 1 毫米。偏移量也与三角形范围和对象空间位置成线性比例。

对于图 4 中的一个例子，在距离世界空间原点 1 公里的 20 米（物体空间原点在根部）的树上，在 10 厘米的叶子上产生的二次射线，由于三角形范围、物体空间位置和世界空间位置，偏移幅度将分别为 45 纳米、4µm 和 0.25 毫米。在实践中，‌ 世界空间位置中的舍入误差往往主导所有舍入误差。对于相对较小对象的大型场景尤其如此。

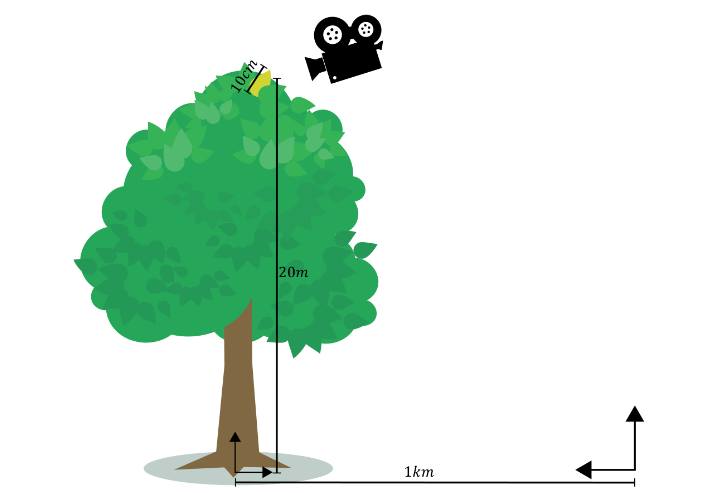
请注意，误差与到场景原点的世界空间距离成比例，而不是与场景摄影机成比例。因此，如果摄影机远离场景原点，则从附近几何体产生的光线的偏移可能会变得过大，导致视觉伪影。

可以通过将整个场景转换到摄影机空间来减少此问题。所有实例都将重新定位，以便摄影机原点与世界空间原点重合。因此变为该相机空间中到相机的距离，并且偏移幅度将与到相机的间距成比例。从摄影机附近的几何体产生的光线将享受相对较小的偏移，从而降低由于偏移而产生视觉伪影的可能性。

连接射线

到目前为止，讨论的重点是偏移光线原点，以防止原点处的自相交。光线和路径跟踪算法还跟踪光线，以评估不同三角形上两点之间的可见性，例如连接着色点和光源的阴影光线。

这些光线可能在光线的任一端发生自相交。有必要偏移两端以避免自相交。端点的偏移以与光线原点类似的方式计算，但使用对象到世界和世界到对象的变换矩阵、端点的重心和三角形顶点，并使用连接光线方向作为入射光线方向。

与散射光线相反，有必要考虑世界中的舍入误差，以在遍历过程中进行对象光线方向变换。从理论上讲，在射线三角形相交测试中也有必要考虑额外的舍入误差，因为射线原点不在端点三角形上。然而，这个额外的误差与世界到对象的误差成亚线性，因此为了简单起见，这些误差被隐式地组合在一起。

对于端点，清单 6 中的世界到对象转换错误计算被替换为（清单 9）。

// connection ray direction 
precise float3 wldDir = wldEndPosition - wldOrigin; 
 
// bound endpoint object-space error due to object-to-world transform 
float4 absOriginDir = (float4)(abs(wldOrigin) + abs(wldDir), 1); 
objEndErr = mad(c2, mul(abs(w2oEnd), absOriginDir), objEndErr); 

在这里wld 原点是世界空间中的连接射线原点。在 DXR 中，射线是使用原点和方向定义的。将偏移直接应用于世界空间方向，而不是偏移端点并重新计算光线方向。对于端点偏移，清单 8 就变成了清单 10。

// offset ray direction along the endpoint normal towards the ray origin 
wldDir = mad(wldEndOffset, wldEndNormal, wldDir) ; 
 
// shorten the ray tmax by 1 ulp 
const float tmax = 0.99999994039f;

将光线长度缩短 1 ulp，以考虑方向计算中的舍入误差。

在实践中，使用廉价的近似偏移启发式方法与基于标识符的自相交拒绝相结合的更简单方法通常足以避免端点自相交。近似偏移将避免大多数端点自相交，而基于标识符的命中拒绝将照顾剩余的自相交。

对于二次散射光线，请避免基于标识符的自相交拒绝，因为这需要为光线上的每个相交调用任意命中着色器，从而增加显著的性能开销。然而，对于可见性光线，基于端点标识符的命中拒绝的额外性能开销是最小的。

对于使用RAY_FLAG_ACCEPT_FIRST_HIT_AND_END_SEARCH标志时，最多会有两个额外的报告命中：被拒绝的端点自交叉和任何阻塞终止遍历。

对于不使用RAY_FLAG_ACCEPT_FIRST_HIT_AND_END_SEARCH标志，自相交可以在最近命中着色器中拒绝，而不是在任何命中着色器中。如果可见性光线调用端点三角形的最近命中着色器，则未找到更近的命中，因此该命中应简单地视为最近命中着色器中的未命中。

结论

本文提出的方法为二次光线的自相交提供了一个稳健且易于使用的解决方案。该方法应用最小的保守偏移，解决了自相交伪影，同时减少了漏光伪影。此外，该方法具有最小的运行时开销，并且易于在常见的着色管道中集成。虽然这篇文章描述了 DXR 的 HLSL 实现，但该方法很容易转换为 Vulkan 的 GLSL 和 OptiX 的 CUDA 。

想要获取更多信息，请访问 NVIDIA/self-intersection-avoidance 在 GitHub 上查看 HLSL 和 GLSL 示例实现。同时，您也可以查看 OptiX Toolkit ShaderUtil Library，这是一个用于自交叉避免的现成 OptiX 头库。