数据科学家经常把金融界当作测试新技术的游乐场。金融数据已经被记录了几十年,而且都是数字形式的,因此很容易处理。另外,你总是有机会创造一个赚钱的模型!
在金融领域,投资的总体目标是最大限度地提高回报(投资的收益或损失),同时最小化风险(实际结果与预测结果不同的可能性)。简而言之,投资就是数学。
这篇文章介绍了一种投资组合优化策略,可以帮助最小化风险敞口。有了 GPU ,算法的速度可以提高 66 倍。
对于散户投资者来说,这种加速对于频繁的再平衡尤其有用。同时,机构投资者可以通过机器人顾问使用这种算法来管理资金。为每个独特客户的投资组合重新计算算法的计算成本可能会很高,通过引入 GPU 可以大大降低计算成本。
在这篇文章中,我将一步一步地介绍使用分层风险平价( HRP )进行有效投资组合分配的 ML 技术。本例将 Python 用于 RAPIDS 。
选择有效财务预测的算法
1952 年,哈里·马科维茨( Harry Markowitz )引入了一种被称为现代投资组合理论的投资组合优化模型。该模型可以生成一个投资组合,在给定的风险水平下实现收益最大化。
不幸的是,故事并没有就此结束。马科维茨的现代投资组合理论只有在你知道每种股票的风险和回报的情况下才能产生最有效的投资组合。然而,这种情况并不总是发生,因为过去的表现并不代表未来的结果。
什么是分层风险平价?
2016 年,马科斯·洛佩斯·德普拉多在他的论文 建立多样化的投资组合,在样本之外表现良好 中介绍了 HRP 。该算法背后的想法是使用 machine learning 技术,这样股票只需与类似股票竞争投资组合中的现货。
例如, Verizon 股票与 AT & T 高度相关。因此, Verizon 只与 AT & T 等股票竞争代表权,而不是与每个行业的所有股票竞争。
HRP 投资组合分配分步指南
在本文的其余部分中,我重点介绍了在 RAPIDS 上实现 HRP ,然后将其性能与其他常用技术进行比较。
获取数据
在这篇文章中,我使用了从 2018 年 11 月到 2021 年 11 月的纳斯达克和纽约证券交易所的每一个证券的每日调整后的收盘数据。该数据集是通过 NVIDIA/fsi-samples GitHub repo 的脚本获得的
在硬件方面,我使用了带有 NVIDIA Quadro 8000 GPU 的 i7 CPU 。对于软件,我使用了 Python 3.9 和 RAPIDS 22.02 。
争论数据
首先读取数据集,并将其聚合到名为 m 的数据帧中。抛售任何空值股票。
import cudf
m1 = cudf.read_csv("MVO3.2021.11/NASDAQ/prices.csv")
m2 = cudf.read_csv("MVO3.2021.11/NYSE/prices.csv")
m = cudf.concat([m1, m2], axis = 1)
m = m.dropna(axis = 1)
一些证券表现不佳:一些证券多年保持不变,另一些证券包含非正值。移除这些不良证券。
data = m.values # data.shape = (days, nAssets) days = data.shape[0] logRetAll = cp.log(data[1:, :]/data[:-1, :]) moveMask = cp.count_nonzero(logRetAll, axis = 0) > (days * 0.9) # Require that each security moves day to day at least 90% of the time positiveMask = data.min(axis = 0) > 0 # Require that all the data is positive mask = moveMask & positiveMask data = data[:, mask] logRetAll = logRetAll[:, mask]
接下来,将 m 分为两部分:培训和测试阶段。培训期为 2018 年 11 月至 2020 年 11 月,测试时间为 2020 年 11 月至 2021 年 11 月。
split = int(days*2/3) train = data[:split, :] test = data[split:, :]
因此,在为训练数据(而不是时间序列数据)创建日志返回矩阵后,可以使用内置的cuDF方法获得相关和协方差矩阵。
# Obtain training cov/corr logRetTrain = logRetAll[:split - 1, :] corrTrain = cp.corrcoef(logRetTrain, rowvar = False) covTrain = cp.cov(logRetTrain, rowvar = False) * 252 # Annualized covariance
执行群集
要将股票聚集在一起,请定义一个度量,给出两个股票之间的距离:
由于相关性的范围是[-1 , 1],你可以看到的范围是
[0, 1],其中意味着
和
是完全相关的,如果
,那么
和
是完全不相关的。
有关是距离度量的完整证明,请参见 洛佩斯德普拉多纸 。
D = cp.sqrt(0.5 * (1 - corr))
现在,您可以计算两个股票之间的距离,对它们进行聚类,以便将相似的股票聚集在一起。
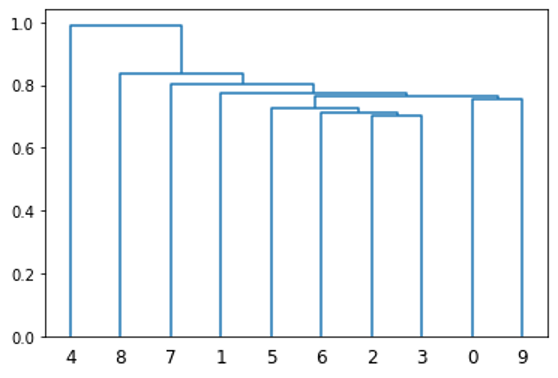
每个项目都放置在自己的簇中,最近的两个簇连接在一起。然后,重新计算这个新簇和所有其他簇之间的距离。同样,将两个最近的簇组合在一起。重复这个过程,直到只有一个集群。可视化这种聚类的一种方法是使用树状图。
from scipy.cluster.hierarchy import linkage, dendrogram dendrogram(linkage(D[:10, :10].get()));
cuML有一个内置的方法来执行此功能,在下面的代码示例中使用。这比 scipy 的链接功能快得多,后者执行类似的功能。
from cuml import AgglomerativeClustering as AC # Create single linkage cluster using the Euclidean metric def cluster(D): model=AC(affinity='l2', connectivity='pairwise', linkage='single') model.fit(D); return model.children_
cluster()输出一个 2 x N 矩阵,其中 N 是中的股票数量。索引
[0, i]和[1, i]表示为 i-th 迭代而加入的集群的索引。
使用矩阵序列化
接下来,从这个集群中生成一个排序,像证券这样的地方彼此靠近。例如,图 2 的 x 轴根据前 10 只股票的聚类情况提供了它们的排序。这是通过矩阵序列化的迭代实现实现的,这是考古学中常用的一种技术。
def seriation(Z): N = Z.shape[1] stack = [2*N-2] res_order = [] while(len(stack) != 0): cur_idx = stack.pop() if cur_idx < N: res_order.append(cur_idx) else: stack.append(int(Z[1, cur_idx-N])) stack.append(int(Z[0, cur_idx-N])) return res_order
图 3 显示了得到的相关矩阵。
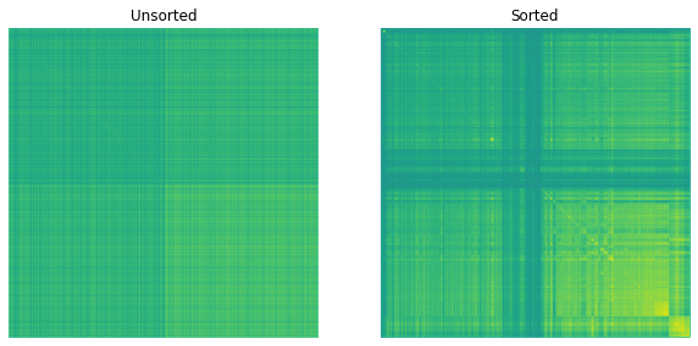
在图 3 中,当您将排序应用于相关矩阵时,可以观察到矩阵中出现的模式。这表明类似的股票彼此接近。
分配权重
最后,给股票分配权重。这是通过递归算法实现的。
将排序后的协方差矩阵一分为二,计算每一半的风险调整量,然后根据逆方差组合( IVP )方法为每一半分配权重。然后每一半重复这些步骤。
IVP 产生的权重与股票的风险量或方差成反比。也就是说,高风险股票的代表性较低,而低风险股票的代表性较高。
HRP 和 IVP 都是风险平价算法:它们只考虑基于过去表现的风险。
def recursiveBisection(V, l, r, W): #Performs recursive bisection weighting for a new portfolio #V is the sorted correlation matrix #l is the left index of the recursion #r is the right index of the recursion #W is the list of weights if r-l == 1: #One item return W else: #Split up V matrix mid = l+(r-l)//2 V1 = V[l:mid, l:mid] V2 = V[mid:r, mid:r] #Find new adjusted V V1_diag_inv = 1/cp.diag(V1) V2_diag_inv = 1/cp.diag(V2) w1 = V1_diag_inv/V1_diag_inv.sum() w2 = V2_diag_inv/V2_diag_inv.sum() V1_adj = w1.T@V1@w1 V2_adj = w2.T@V2@w2 #Adjust weights a2 = V1_adj/(V1_adj+V2_adj) a1 = 1-a2 W[l:mid] = W[l:mid]*a1 W[mid:r] = W[mid:r]*a2 W = recursiveBisection(V, l, mid, W) W = recursiveBisection(V, mid, r, W) return W
分析权重
您现在拥有执行 HRP 所需的所有工具。看看它的表现吧!
#Obtain the final weights and plot them
N = len(res_order)
V = covTrain[res_order, :][:, res_order]
W_tmp = recursiveBisection(V, 0, N, cp.ones(N))
W = cp.empty(len(W_tmp))
W[res_order] = W_tmp
plt.plot(W.get())
plt.xlabel("Security Index")
plt.ylabel("% allocation")
plt.title("HRP Allocation")
plt.plot();
应用列出的方法后,您将得到一个变量 W ,该变量表示每个安全性的权重。
图 4 显示了结果。
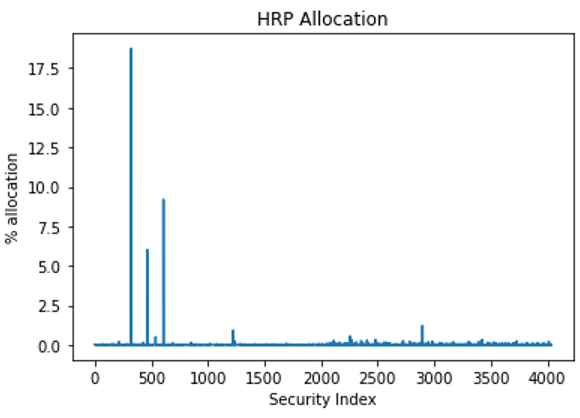
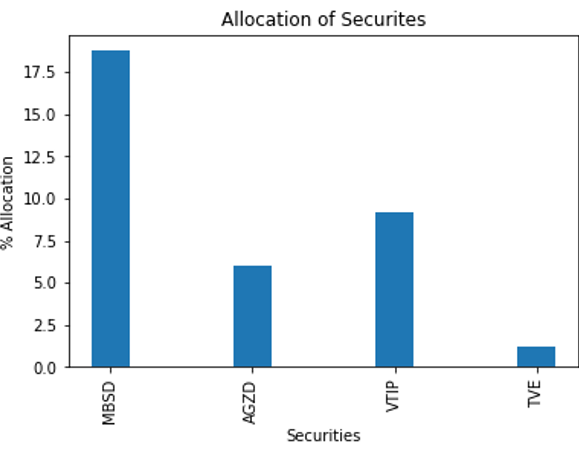
这张图表很难读懂。您可以截断它,以便只显示权重大于 1% 的证券(图 5 )。
作为一个健全性检查,图 6 显示了在培训期间排名靠前的选手的表现。您希望确保证券的波动性相对较低。
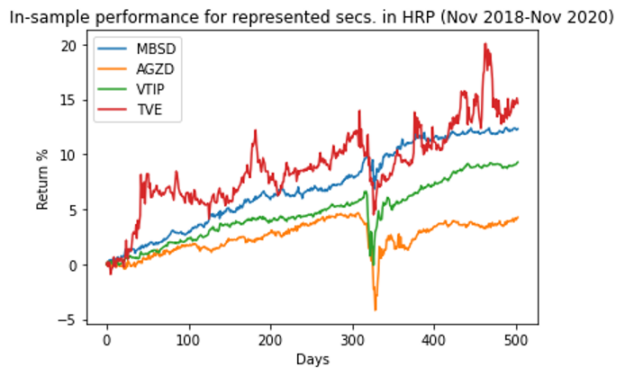
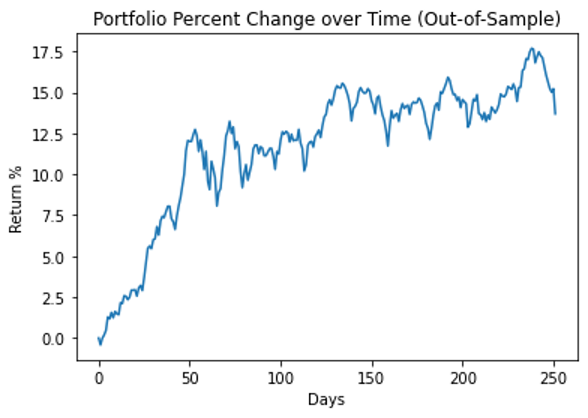
图 7 显示了整个投资组合在测试期间的性能。
与其他投资组合相比
你可以将这种表现与现代投资组合理论进行比较。在这个迭代中,我选择了最大化夏普比率:一个跟踪投资组合绩效的指标。
在这个公式中, 是无风险回报率。在金融界,风险被定义为
,其中
是协方差矩阵。这样一来,投资组合的风险和回报都被纳入衡量标准。
使用 scipy 执行数值优化。
from scipy.optimize import *
from scipy.optimize import *
def MPT(cov, R): cons = [{'type': 'eq', 'fun': lambda x: sum(x) - 1}, #sum(w)==1", {'type': 'ineq', 'fun': lambda x: x}] #each weight >=0 (no short selling)" res = minimize(lambda x: -(x@R-1.025)/sqrt(x.T@cov@x), x0=np.ones(len(R))/len(R), constraints=cons) #Minimize risk" return res.x
这是一个复杂的数值优化问题,尤其是考虑到你有 4000 多个资产。通过要求每种证券的夏普比率必须大于 1 ,将其缩减为 278 种证券。这种切断是任意的,但建议屏蔽以减少运行时间。
W_MPT = cp.zeros(nAssets) sharpeTrain = (trainRetAll - 1.025) / (cp.std(logRetTrain, axis = 0) * math.sqrt(252)) # Annualized sharpe covnp = covTrain[sharpeTrain > 1, :][:, sharpeTrain > 1].get() # Numpy version of covariance matrix over training period, masked Rnp = trainRetAll[sharpeTrain > 1].get() # Return of all stocks over the training period, masked, in numpy W_MPT[sharpeTrain > 1] = MPT(covnp, Rnp, 1+i/100)
您还可以为反向方差投资组合生成权重。
invVarTrain = 1 / cp.var(logRetTrain, axis = 0) W_IVP = invVarTrain / invVarTrain.sum()
最后,生成一些随机投资组合,选择 15 种不同的证券,并随机分配给每种证券。这模拟了不知情的散户投资者可能选择的投资组合。
图 8 显示了所有投资组合的结果。
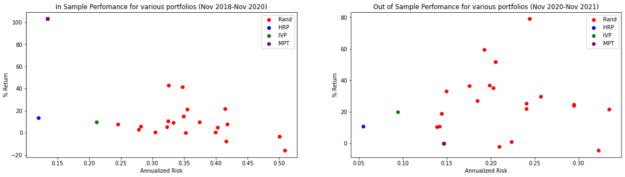
对于前面的投资组合,您可以在下表中生成夏普比率。
| Train (Nov 2018 – Nov 2020) | Test (Nov 2020 – Nov 2021) | |
| Median of Random Portfolios | 0.01 | 0.97 |
| HRP | 0.91 | 1.51 |
| IVP | 0.35 | 1.83 |
| MPT | 7.51 | -0.18 |
虽然 MPT 在培训样本期间的夏普比率较高,但在培训期间,它会变为负值,这意味着投资组合的表现低于 2.5% 的无风险利率。这就证明了所谓的马科维茨诅咒:虽然它在样本中表现最佳,但它往往与样本完全不同。
此外,虽然 IVP 在测试期间的夏普比率高于 MPT ,但请记住,这两种方法都是 risk-parity 组合。他们的目标是将风险降至最低,不考虑回报。值得注意的是,在测试期间, HRP 的风险为 5.5% ,而 IVP 的风险为 9.4% 。
分析速度
另一个需要分析的是运行时与 CPU 的比较。您可以使用 SciPy 、 pandas 或 NumPy 等库而不是 RAPIDS 来重新创建算法。
随着分析的证券数量的增加,所需的计算能力也会增加。这也增加了并行化的能力, GPU 可以捕获并行化。
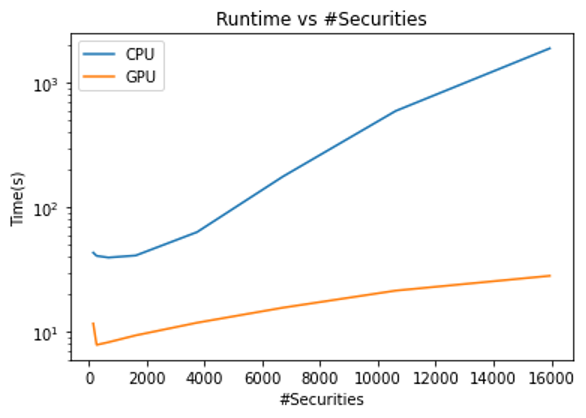
对于最大数量的证券,通过在 CPU 上运行 GPU 可以实现 66 倍的加速!即使在最坏的情况下,您仍然可以获得 4 倍的加速比。
人力资源规划的关键经验
尽管 HRP 最初是为了演示机器学习如何应用于投资组合优化,但与反向方差相比,它可能会降低风险,并比现代投资组合理论具有更高的夏普比率。洛佩斯·德·普拉多在他的 建立多样化的投资组合,其表现优于样本之外的投资组合 论文中进一步证实了这一点,证明合成数据的提取率和方差较低。
投资者在寻找管理风险的方法或与其他金融技术相结合以降低所需回报率的风险时,可能会求助于 HRP 。
借助于 RAPIDS 提供的 GPU 加速, HRP 可以以相对较低的计算成本成为可行的投资组合优化工具。