Related Resources
数据中心/云端

使用 nvmath-python 实现 Epilog 运算与矩阵乘法的融合计算

2024年 11月 18日
By
0

nvmath-python (Beta) 是一个开源 Python 库，为 Python 程序员提供对 NVIDIA CUDA-X 数学库的高性能数学运算访问。nvmath-python 既提供底层库的低级绑定，也提供更高级别的 Python 抽象。它可与 PyTorch 和 CuPy 等现有 Python 软件包进行互操作。

在本文中，我将展示如何在 nvmath-python 中将 结语 与矩阵乘法结合使用。结语是可以与正在执行的数学运算（如 FFT 或矩阵乘法）融合的运算。可用的结语涵盖了大多数常见的深度学习计算。我通过实施简单神经网络的常见正向和反向传递运算来演示其用法。

要安装 nvmath-python，请 按照安装说明 操作。

使用 RELU_BIAS 后记优化正向传递

在本节中，我将演示如何使用 epilogs 实现简单线性层的前向传递。此层首先将输入向量乘以权重矩阵，然后向生成矩阵的每个元素添加偏差，最后应用 ReLU 激活函数。

ReLU 是修正线性单元的简称，是一种常用的激活函数，可以在保持正值不变的同时将负值替换为 0。

在矩阵运算方面，该层可以表示为：

relu(Wx + B)

在方程中，以下定义成立：

  • x 是一批形状为的输入向量 n \times b:
    • n 是层的输入数量。
    • b 是批量大小。
  • W 是形状的权重矩阵 m \times n:
    • m 是层的输出数量。
    • n 是其输入的数量。
  • B 是长度为 m 的偏置向量，将其添加到生成矩阵的每一列中。

假设您的输入、权重和偏差为 CuPy 数组：

num_inputs, num_outputs = 784, 100
batch_size = 256
 
weights = cupy.random.rand(num_outputs, num_inputs)
bias = cupy.random.rand(num_outputs)
x = cupy.zeros((num_inputs, batch_size))

在最基本的版本中，您可以通过使用 nvmath-python 计算 Wx，然后手动处理偏差和 ReLU 来实现此线性层，如下代码示例所示。

在本示例中，我使用 nvmath.linalg.advanced.Matmul -class.html” rel=”follow noopener” target=”_blank”>有状态 API ，其中您可以将初始化和规划与乘法的实际执行分开。当您必须执行多个类似的乘法运算时，我推荐这种方法，因为它可以让您分期偿还规划的初始成本。有关 Matmul 的更多信息，请参阅 nvmath.linalg.advanced.Matmul。

mm = Matmul(weights, x)
mm.plan()
 
def forward():
    y = mm.execute()
    y += bias[:,cupy.newaxis]
    y[y < 0] = 0
    return y

要提高代码的性能，请利用 RELU_BIAS epilog 在单个融合的 cuBLAS 操作中执行所有三个操作。这个结语首先将偏差添加到乘法结果中，然后应用 ReLU 函数。

您可以使用 Matmul.plan 方法的 epilog 参数指定结语。一些结语（包括 RELU_BIAS）会接收额外的输入，可在 epilog_inputs 字典中指定。有关结语的更多信息，请参阅 nvmath.linalg.advanced.Matmul 。

from nvmath.linalg.advanced import MatmulEpilog
 
mm = Matmul(weights, x)
mm.plan(epilog=MatmulEpilog.RELU_BIAS, epilog_inputs={"bias": bias})
 
def forward():
    y = mm.execute()
    return y

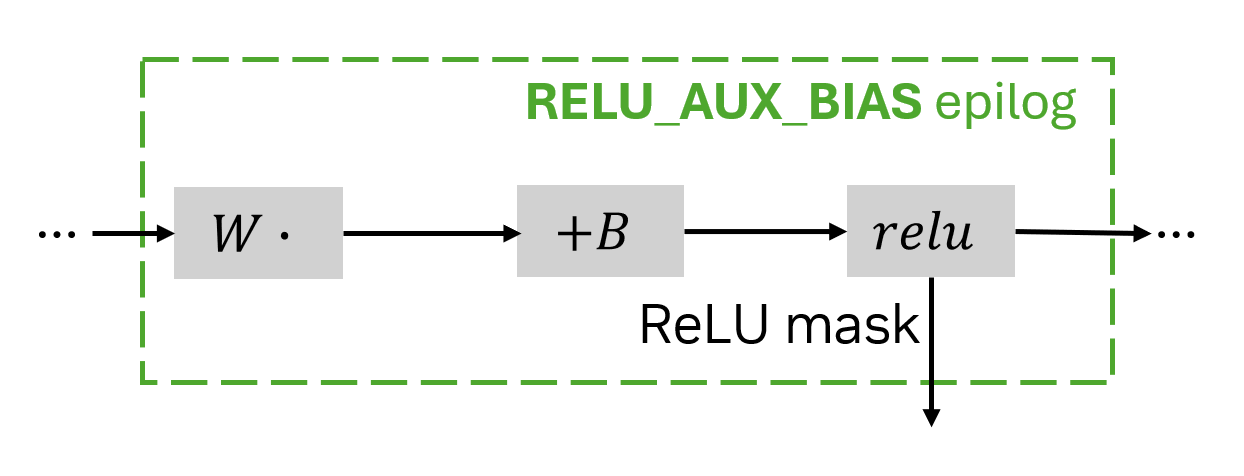
正如我稍后解释的那样，要通过 ReLU 函数进行反向传播，您必须知道向 ReLU 的哪些输入为正、哪些为负。此辅助信息称为 ReLU 掩码 ，可通过 RELU_AUX_BIAS 后记获得。

当使用带有辅助输出的结语时，Matmul.execute 将返回一个包含实际结果和辅助输出字典的元组。在 RELU_AUX_BIAS 的情况下，辅助输出字典只有一个键 relu_aux，其中包含 ReLu 掩码。该掩码是位编码的，可能难以读取，但在向后传递期间，有专门的结语可以为您执行此操作。

from nvmath.linalg.advanced import MatmulEpilog
 
mm = Matmul(weights, x)
mm.plan(epilog=MatmulEpilog.RELU_AUX_BIAS, epilog_inputs={"bias": bias})
 
relu_mask = None
 
def forward():
    global relu_mask
    y, aux_outputs = mm.execute()
     relu_aux = aux_outputs["relu_aux"]
    return y
A block diagram shows the operations of a forward pass: multiplication by the weights, addition of bias and application of ReLU. Matmul with RELU_AUX_BIAS epilog is handling all three operations, and producing the ReLU mask as an auxiliary output.
图 1、Matmul 在 RELU_AUX_BIAS 后记中介绍的前向传递操作

使用 RELU_AUX_BIAS epilog 的实现速度比其朴素的实现要快，从而显著提升性能。

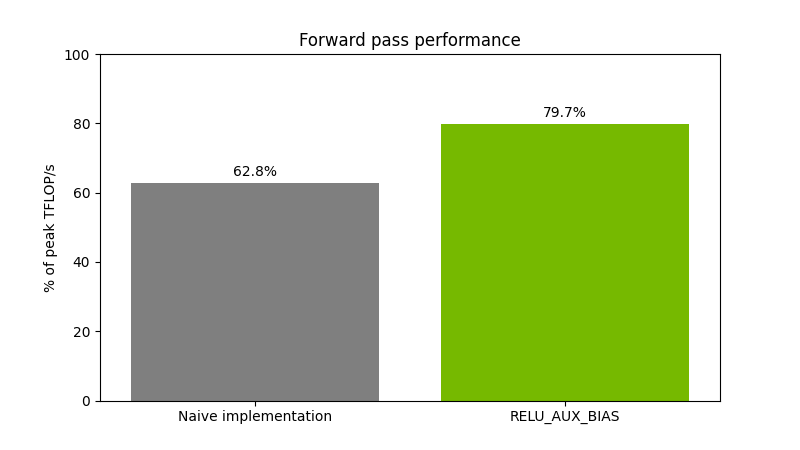
A bar plot showing the performance of the naive implementation and RELU_AUX_BIAS. Naive implementation reaches 62.8% of peak TFLOP/s, and RELU_AUX_BIAS reaches 79.7%.
图 2. 前向传播实现的性能比较

图 2 显示了对大小为（65536，16384）（16384，8192）的 float16 矩阵执行矩阵乘法运算，然后执行偏加和 ReLU 运算。性能在 NVIDIA H200 GPU 上进行测量。

使用 DRELU_BGRAD 后记优化反向传播

在神经网络的反向传播过程中，损失函数相对于输出的梯度会反向传播到网络层，以计算每个参数的梯度。

直观地说，对于每个操作，当其输出对损失的影响已知时，就有可能确定其输入和参数（例如权重矩阵中的值）如何影响损失。有关更多信息，请参阅 反向传播 。

在这一部分，我假设有多个线性层堆叠在一起。我对通常被认为属于不同层的操作序列实施反向传播：添加偏差、应用 ReLU 以及乘以权重。

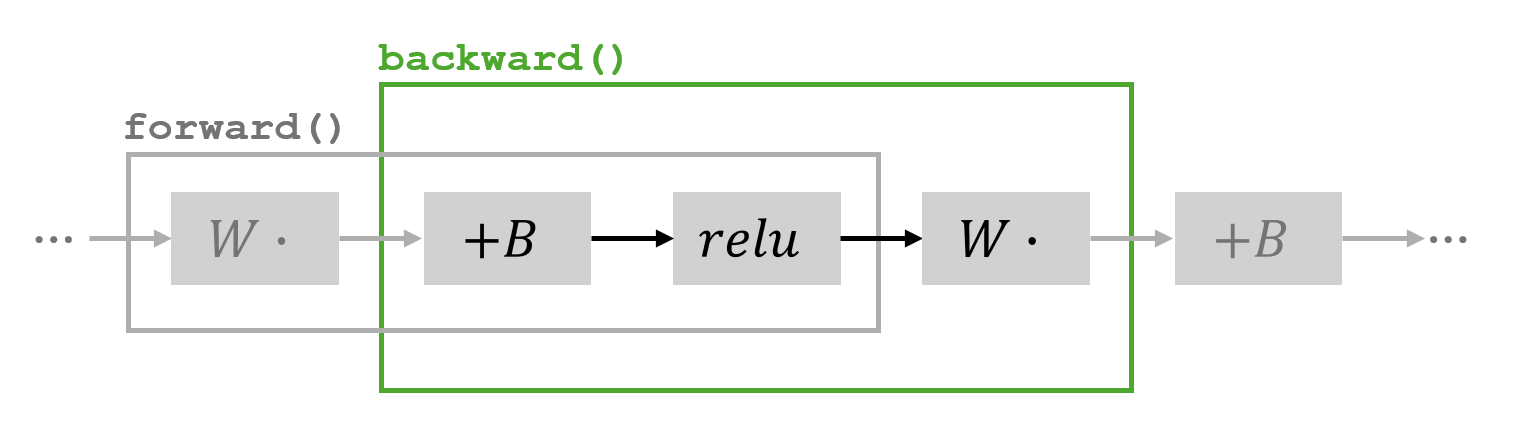
A block diagram shows the operations of a forward pass with multiple linear layers: multiplication by weights, adding bias, applying ReLU, multiplying by weights, adding bias, and so on. The backward pass box covers adding bias, applying ReLu, and multiplying by weights.
图 3. 在 forward 中实施的操作以及 backward 中涵盖的部分

让 t_0 作为前面显示的网络部分的输入，并分别通过 t_1、t_2 和 t_3 显示中间结果：

  • t_1 = x + B
  • t_2 = relu(t_1)
  • t_3 = Wt_3

在反向传播中，当您知道 loss function L 是如何受 t_3（即 \frac{\partial L}{\partial t_3}）影响时，即可计算相对于其他参数的梯度。如需详细了解用于计算梯度的公式的推导，请参阅 Automatic Differentiation 和 Neural Networks 。

  • \frac{\partial L}{\partial W} = t_2^T \frac{\partial L}{\partial t_3}
  • \frac{\partial L}{\partial t_2} = W^T \frac{\partial L}{\partial t_3}
  • \frac{\partial L}{\partial t_1} = 0，其中 t_1 为负值，\frac{\partial L}{\partial t_1} = \frac{\partial L}{\partial t_2}，其中 t_2 为非负值（ReLU 掩码包含此信息）
  • \frac{\partial L}{\partial B} 是 \frac{\partial L}{\partial t_1}，按批量维度求和
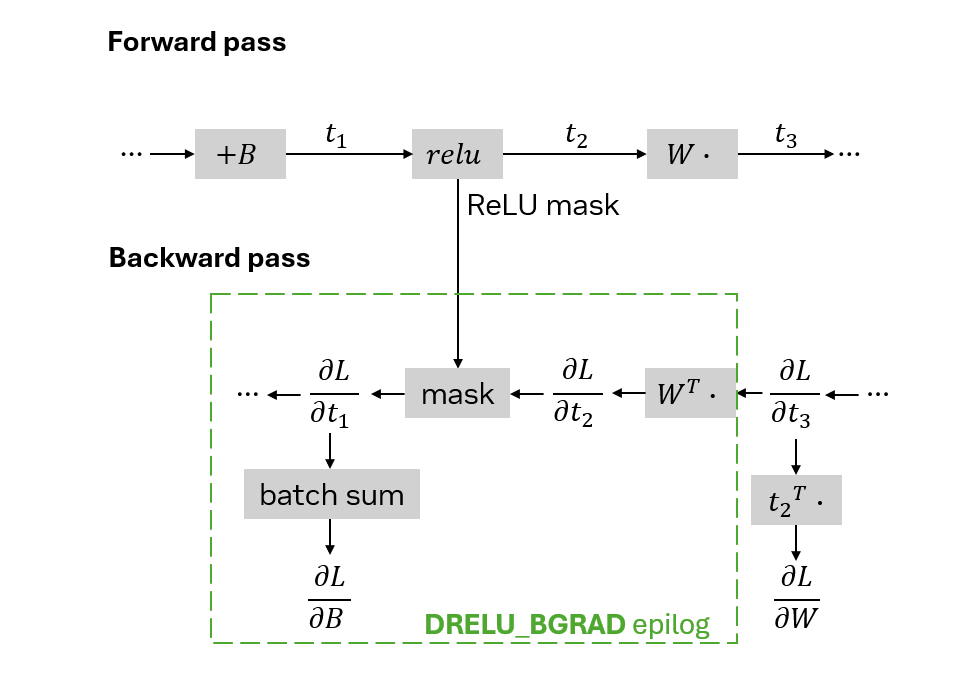
A block diagram shows the operations of a forward pass and backward pass, with the formulas for gradients. Matmul with DRELU_BGRAD epilog covers computing the gradients for t2 (multiplying by weights), t1 (applying ReLU mask) and B (batch sum). Computing the gradients for W is not covered by the DRELU_BGRAD epilog.
图 4. 向后传递的操作，DRELU_BGRAD 结束语包含的操作

计算 \frac{\partial L}{\partial B} 和 \frac{\partial L}{\partial t_1} 所需的运算可以通过使用仅用于矩阵乘法的 Matmul，然后手动处理掩码和批量和来简单实现。

mm = Matmul(weights.T, grad)
mm.plan()
 
def backward():
    grad_t1 = mm.execute()
    grad_t1[mask] = 0  # assuming that `mask = (t1 < 0)`
    grad_bias = cupy.sum(grad_t1, axis=1)
    return grad_t1, grad_bias

要优化您的向后传递，请使用 DRELU_BGRAD 后记。假设梯度 \frac{\partial L}{\partial t_3} 在 CuPy 数组 grad 中可用。DRELU_BGRAD 的 epilog 需要一个输入 relu_aux，其中包含从 RELU_AUX_BIAS 的 epilog 返回的掩码。它将此遮罩应用于乘法结果。它还会返回一个辅助输出，其中包含结果的逐列总和，恰好是 \frac{\partial L}{\partial B}。

mm = Matmul(weights.T, grad)
mm.plan(epilog=MatmulEpilog.DRELU_BGRAD, epilog_inputs={"relu_aux":relu_mask})
 
def backward():
    grad_t1, aux_outputs = mm.execute()
    grad_bias = aux_outputs["drelu_bgrad"]
    return grad_t1, grad_bias
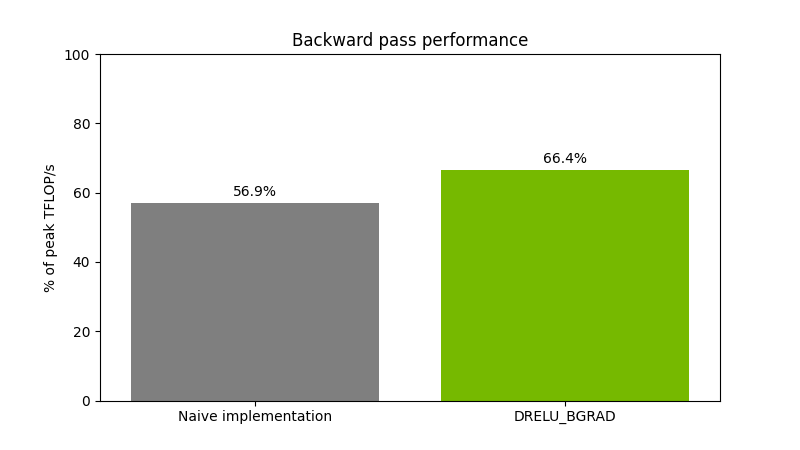
A bar plot shows the performance of the naive implementation and DRELU_BGRAD. Naive implementation reaches 56.9% of peak TFLOP/s, and DRELU_BGRAD reaches 66.4%.
图 5. Performance comparison of backward pass implementations

图 5 显示了对大小为（65536，16384）（16384，8192）的 float16 矩阵执行矩阵乘法运算，然后应用 ReLU 掩码和偏差梯度计算。该性能在 NVIDIA H200 GPU 上进行了测量。

结束语 

借助 nvmath-python 的后记，您可以在 Python 代码中融合常见的深度学习计算，从而大幅提高性能。有关更多信息，请参阅 nvmath-python：在 Python 文档中充分发挥 NVIDIA Math Libraries 的功能 。

我们是一个开源库，请随时访问 /NVIDIA/nvmath-python GitHub 仓库并与我们联系。

 

 

相关资源

0

标签

数据中心/云端 | 生成式人工智能/大语言模型 | CUBLAS | CUDA | General | Intermediate Technical | Python | 教程 | 数据中心/云 | 深度学习 | 生成型人工智能

关于作者

Szymon Karpiński 是 NVIDIA 数学库团队的软件工程师。他对性能优化和实现高性能 Python 编程感兴趣。
Search