Related Resources
Data Science

ProRL v2를 활용한 장기 학습 기반 LLM 강화학습 확장

2025년 8월 20일
By , , , and
Discuss (0)
Reading Time: 6 minutes

현재 AI 분야에서 가장 흥미로운 질문 중 하나는, 거대 언어 모델(LLM)이 지속적인 강화학습(RL)을 통해 계속 발전할 수 있을지, 아니면 어느 시점에서 성능이 정체될지를 확인하는 일입니다.

NVIDIA Research에서 개발한 ProRL v2는 장기 강화학습(Prolonged Reinforcement Learning, ProRL)의 최신 버전으로, LLM에 대한 장기 RL 학습의 효과를 검증하기 위해 설계되었는데요. 고도화된 알고리즘, 정교한 정규화 기법, 넓은 도메인 커버리지를 바탕으로 ProRL v2는 기존 RL 학습 계획을 훌쩍 넘는 수준까지 모델 성능의 경계를 확장합니다. 수천 단계의 추가 RL 학습을 진행하며, 모델이 실제로 의미 있는 성능 향상을 이룰 수 있는지 체계적으로 실험했습니다.

이번 포스트에서는 최근 공개된 ProRL v2의 핵심 기술과 주요 기법을 소개하고, 최신 실험을 통해 확인된 성능 결과를 공유합니다. 이를 통해 LLM이 어떻게 지속적으로 학습하고 성장할 수 있는지 그 가능성을 함께 살펴볼 것입니다.

ProRL v2는 어떻게 RL 확장을 가능하게 할까요?

생각의 사슬(Chain-of-thought) 프롬프트나 트리 탐색 같은 기법은 모델이 이미 가진 지식을 더 효과적으로 활용하도록 도와줍니다. 반면, 강화학습(RL)은 특히 코드로 검증 가능한 엄격한 보상 체계를 갖출 경우, 모델을 완전히 새로운 영역으로 확장시킬 잠재력을 가지고 있습니다. 하지만 기존의 단기 지향적 RL 방식은 학습 불안정성과 빠른 성과 한계에 부딪히곤 했으며, 종종 ‘출력 온도 조절에 불과한 파인튜닝(fine-tuning)’으로 여겨지곤 했습니다.

ProRL은 이 기존 구조에 근본적인 변화를 제안합니다. 주요 특징은 다음과 같습니다:

  • 장기 학습: 5개 도메인에서 3,000단계 이상의 RL 학습을 통해 1.5B 파라미터 모델 중 최고 수준의 성능 달성
  • 안정성과 견고함: KL 정규화 기반 신뢰 영역, 주기적인 기준 정책 초기화, 출력 길이에 대한 정규화 계획 적용
  • 검증 가능한 보상: 모든 보상 신호는 코드로 정의되며, 항상 검증 가능
  • 간결함 유지: 스케줄 기반 코사인 길이 패널티로 출력의 효율성과 간결함 확보

ProRL v2의 목표는 익숙한 해답을 단순히 다시 뽑아내는 데 그치지 않고, 모델이 스스로 발견할 수 있는 영역을 진정으로 넓혀 가는 데 있습니다.

기존 RL 파인튜닝(fine-tuning)ProRL v2
수백 단계, 단일 도메인 (Few-hundred steps, one domain)3,000+ 단계, 다섯 도메인 (3,000+ steps, five domains)

엔트로피 붕괴, KL 급등 (Entropy collapse, KL spikes)		PPO-Clip, REINFORCE++ baseline, Clip-Higher, Dynamic Sampling, 기준 정책 리셋

불안정한 보상 모델 드리프트 (Risky reward model drift)		완전히 검증 가능한 보상 (Fully verifiable rewards)
장황하고 긴 출력 (Verbose, lengthy outputs)스케줄 기반 코사인 길이 패널티 (Scheduled cosine length penalty)
표 1. ProRL 레시피와 기존 RL 파인튜닝 비교

핵심 기술: ProRL 알고리즘과 정규화 기법

ProRL v2는 REINFORCE++ 베이스라인을 기반으로 구축되었습니다. 이 베이스라인은 로컬 평균과 글로벌 배치 단위의 어드밴티지 정규화를 적용해 RLVR 학습의 안정성을 높이며, Clip-Higher 기법으로 탐색을 장려하고 Dynamic Sampling으로 노이즈를 줄여 학습 효율을 개선합니다. 여기에 더해 ProRL v2는 다음과 같은 혁신적인 기법을 도입했습니다.

  • 출력의 간결함을 유지하기 위한 스케줄 기반 코사인 길이 패널티
  • 과적합 방지 및 안정성 유지를 위한 KL 정규화된 trust region과 주기적인 reference 정책 초기화 (현재 최고 성능 체크포인트 기준)

REINFORCE++ 기반의 근접 정책 최적화 (Proximal Policy Optimization, PPO)

ProRL의 핵심에는 클리핑된 근접 정책 최적화(PPO-Clip) 손실 함수가 있습니다. 이 방식은 새로운 정책이 기존 정책에서 지나치게 멀어지지 않도록 제한해, 학습 과정에서 정책 업데이트의 안정성을 확보합니다.

Where:

  • r_\theta(\tau) = \frac{\pi_\theta(\tau)}{\pi_{\text{old}}(\tau)}
  • \tilde{R}_\tau = R_\tau - \mu_{\text{group}}  
  • \mu_{\text{group}} = \text{mean}_{\text{group}}(R_\tau)
  • A(\tau) = \frac{\tilde{R}\tau - \mu_{\text{batch}}}{\sigma_{\text{batch}}} 
  • \mu_{\text{batch}} = \text{mean}_{\text{batch}}(\tilde{R}_\tau)
  • \sigma_{\text{batch}} = \text{std}_{\text{batch}}(\tilde{R}_\tau)

여기서 ‘group‘은 동일한 프롬프트에 대해 생성된 응답 전체를 의미하며, group normalization에 사용됩니다.

REINFORCE++ 베이스라인에서의 Global Batch Normalization은 작은 그룹 크기 때문에 발생할 수 있는 가치 불안정을 완화합니다. 먼저 소규모 그룹의 평균 보상을 빼내어 보상 분포를 재구성하고, 이를 통해 알고리즘이 단순한 보상 패턴(예: 0=오답, 1=정답, -0.5=형식 보상)에 둔감해지지 않도록 합니다. 그 후, 전체 배치 단위에서 정규화를 적용합니다.

클리핑 범위:

Clip-Higher와 Dynamic Sampling

Clip-Higher는 PPO 클리핑 범위의 상한을 더 높여, 정책 엔트로피가 붕괴하는 현상을 완화하고 샘플링 다양성을 유지하도록 합니다 ( ).

Dynamic Sampling은 모든 응답이 전부 정답(1) 또는 전부 오답(0)인 그룹 프롬프트를 학습에서 제외해, 그래디언트 추정 과정의 노이즈를 줄이고 학습 효율을 높입니다.

스케줄 기반 코사인 길이 패널티

출력을 간결하게 유지하고 토큰 사용 효율을 높이기 위해, 스케줄 기반의 코사인 형태 길이 패널티가 적용됩니다.

Where:

  • t = 현재 출력 길이 (토큰 수)
  • T = 컨텍스트 토큰 제한
  • \eta_\text{min}, \eta_\text{max} = 보상/패널티 경계값

보상 업데이트

길이 패널티는 일정 주기로 on/off를 반복하여(예: 100단계 on, 500단계 off) 이를 통해 정보성(informativeness)과 간결성(conciseness) 사이의 균형을 유지합니다.

KL 정규화 및 레퍼런스 정책 초기화

KL 패널티는 정책이 기준(reference) 정책에서 지나치게 멀어지지 않도록 제약을 걸어 학습의 안정성을 유지합니다. 또한 주기적인 리셋을 통해 과적합을 방지하고 학습의 일관성을 확보합니다:

REINFORCE++ 베이스라인에서는 KL divergence를 k₂ 추정기로 정규화합니다:

여기서:

clamp(z,−10,10) 함수는 zzz 값을 [−10,10][-10, 10][−10,10] 범위로 제한해 수치적 안정성을 확보합니다.

레퍼런스 리셋

매 200~500 RL 스텝마다(또는 KL 급등이나 검증 정체 시), 기준 정책 ​는 현재 정책으로 리셋되며, 옵티마이저 상태는 초기화되지 않습니다.

기준 정책을 정기적으로 리셋함으로써, 모델은 오래된 기준 정책에 제약받지 않고 효과적으로 학습을 계속할 수 있습니다.

주기적으로 적용되는 스케줄 기반 코사인 길이 패널티도 중요한 역할을 합니다. 패널티를 주기적으로 켜고 끔으로써, 모델이 짧거나 고정된 컨텍스트 길이에 갇히는 것을 방지하고, 출력의 정확도와 토큰 효율성을 모두 개선할 수 있습니다. 이 두 가지 전략은 모델이 기준 정책이나 컨텍스트 길이에 의해 제한되는 것을 막아주며, 시간이 지남에 따라 정확도와 전반적인 성능의 지속적인 개선을 지원합니다.

LLM에 RL을 확장하면서 발견한 점

새로운 최신 성능, 지속적인 개선, 새로운 해법, 그리고 한계 돌파를 확인했습니다.

  • 최신 최고 성능: RL 학습 단계를 늘릴수록 성능이 꾸준히 개선되며, ProRL v2 3K는 1.5B 추론 모델 중 최고 성능을 기록했습니다.
  • 지속적이고 의미 있는 개선: Pass@1과 Pass@k 모두 수천 스텝에 걸쳐 꾸준히 상승해, 베이스 모델의 추론 한계를 넓혔습니다.
  • 창의적이고 새로운 해법: ProRL 출력은 사전학습 데이터와의 n-그램 중복도가 낮아, 단순 암기보다 진짜 ‘창의성’이 반영된 결과를 보여줍니다.
  • 성능 한계 돌파: 기존 모델이 항상 실패했던 문제에서도 ProRL은 높은 정답률을 달성했으며, 분포 바깥(out-of-distribution) 상황에서도 강한 일반화 능력을 보였습니다.

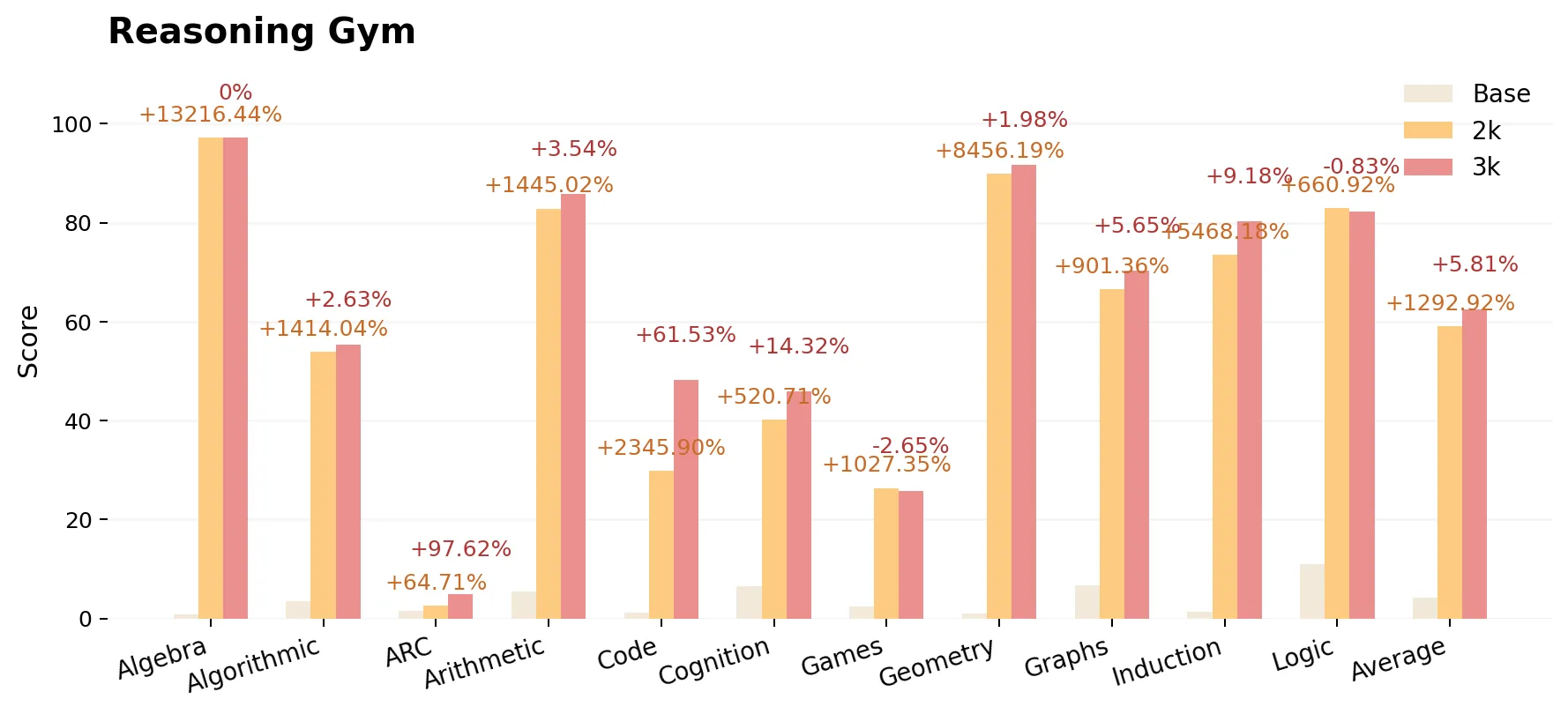
ProRL 종합 성능

ProRL은 수학, 코드 생성, 다양한 reasoning benchmark에서 평가되었습니다. 평가 대상은 다음과 같습니다:

  • Base: DeepSeek-R1-Distill-Qwen-1.5B
  • ProRL v1 2K: 2,000단계 RL 학습 (16K context)
  • ProRL v2 3K: 3,000단계 RL 학습 (8K context)

글 작성 시점 기준으로도 모델은 계속 학습 중이며 정확도 역시 지속적으로 개선되고 있습니다. 아래 수치는 2K 모델이 베이스 모델 대비 얼마나 향상되었는지, 또 3K 모델이 2K 대비 얼마나 향상되었는지를 보여줍니다. 특히 context 길이를 절반으로 줄였음에도(16K → 8K), 전반적인 정확도는 모든 작업에서 개선되었습니다.

그림 1. 수학 및 IFEVAL 벤치마크의 모든 작업에서 2K-step 모델은 베이스 모델보다 월등히 우수하며, 3K-step 모델은 2K-step 모델보다 더욱 우수합니다.
그림 2. 코드 생성 벤치마크의 모든 작업에서 2K-step 모델은 베이스 모델보다 현저히 우수한 성능을 보이며, 3K-step 모델은 2K-step 모델보다 더욱 우수한 성능을 보입니다.
그림 3. Reasoning Gym 벤치마크에서 2K 단계 모델은 베이스 모델보다 우수한 성능을 보이며, 3K 단계 모델은 2K 단계 모델보다 더욱 우수한 성능을 보입니다.
그림 4. 성능 개선 외에도 2K 단계 모델은 출력 길이를 17.54% 줄여 더 효율적인 추론을 가능하게 합니다.

맺음말

실험 결과는 수학, 코드, 추론과 같은 과제에서 LLM이 장기 강화학습(RL)을 통해 지속적인 성능 향상을 달성할 수 있음을 확인할 수 있었습니다. 기존의 일반적인 학습 방식보다 훨씬 뛰어난 성과를 내며, 도전적인 과제와 분포 바깥 문제에 대해서도 강인한 성능을 보였는데요. 이는 장기 RL 학습이 모델의 추론 능력을 실제로 확장할 수 있음을 보여줍니다.

  • 최신 최고 성능을 기록한 1.5B 추론 모델 ProRL v2 3K는, 베이스 모델 DeepSeek-R1-1.5B를 크게 앞섰을 뿐 아니라, 이전 버전 ProRL v1 2K가 달성했던 성과까지 뛰어넘었습니다.
  • ProRL은 수학, 코드, 추론 전반에서 꾸준하고 신뢰할 수 있는 성능 향상을 보여주며, 특히 베이스 모델이 (공격적인 샘플링에도 불구하고) 실패했던 영역에서도 확실한 개선을 입증했습니다.
  • 단순히 모델 규모를 키우는 것보다 RL 학습 단계를 늘리는 것이 경계 확장(boundary expansion)에 훨씬 더 효과적이라는 점도 확인했습니다.
  • 이 성과는 일시적인 우연이 아니라 일관된 경향으로, 거의 모든 하위 과제에서 장기 RL의 이점이 확인되었습니다.

모델 성능의 한계를 넓히거나 LLM의 추론 가능성을 탐구하고자 하는 실무자들에게 ProRL은 재현 가능한 기반과 실질적인 학습 레시피를 제공합니다. 오픈소스 모델과 벤치마크가 공개되어 있으니, 커뮤니티에서도 이를 직접 실험하고 검증하며 LLM을 위한 RL의 한계와 가능성을 함께 탐구해볼 수 있습니다.

지금 바로 시작해보세요. Hugging Face에서 ProRL 모델을 확인하실 수 있습니다.

Discuss (0)

Tags

Data Science | Generative AI | featured | LLM Techniques | NVIDIA Research | Reinforcement Learning | Training AI Models

작성자 소개

Jian Hu 프로필
Jian Hu는 NVIDIA의 시니어 딥러닝 엔지니어로, 대규모 언어 모델(LLM)과 인간 피드백 기반 강화 학습(RLHF)에 집중하고 있습니다. 국립대만대학교에서 컴퓨터공학 석사 학위를 받았고, 이후 홍콩과기대(GZ)에서 박사 과정을 시작했지만 중도에 그만뒀습니다. 컴퓨터 엔지니어링과 머신러닝 분야에서 5년간 경력을 쌓았으며, RLHF 분야에서 주목받는 프로젝트인 OpenRLHF와 REINFORCE++의 제1저자입니다. 관심 분야는 강화 학습, 범용 인공지능(AGI), 그리고 모델과 시스템의 공동 최적화입니다.
Mingjie Liu 프로필
Mingjie Liu는 NVIDIA의 Learning and Perception Research 팀에서 활동하는 시니어 리서치 사이언티스트입니다. 텍사스대학교 오스틴 캠퍼스에서 박사 학위를 받았고, 현재는 강화 학습을 활용해 LLM의 추론 능력과 에이전트 성능을 높이는 연구를 진행 중입니다. 이전에는 ChipNeMo, RTL 코드 생성 등 칩 설계를 위한 도메인 특화 LLM 개발에도 참여했습니다.
Shizhe Diao 프로필
Shizhe Diao는 NVIDIA Research의 연구 과학자이며 파운데이션 모델의 효율적인 훈련 및 조정 연구에 열정을 쏟고 있습니다. Shizhe는 홍콩과학기술대학교에서 박사 학위를 취득했으며, Tong Zhang 교수의 지도를 받았습니다.
Ximing Lu 프로필
Ximing Lu는 NVIDIA의 Language and Cognition Research 팀 소속 리서치 사이언티스트입니다. 워싱턴대학교에서 컴퓨터공학 학사 학위를 받았고, 현재는 데이터 합성, 강화 학습, 에이전트 시스템, 모델 아키텍처, 멀티모달리티 연구에 주력하고 있습니다. NAACL 2022 최우수 논문상, EMNLP 2023 우수 논문상을 공동 수상한 이력이 있습니다.
Yi Dong 프로필
Yi Dong은 NVIDIA에서 자연어 처리/딥 러닝 실제 애플리케이션을 연구하는 선임 응용 과학자입니다. 그는 존스홉킨스 대학교 의과대학에서 컴퓨터 신경과학을 전공하여 박사 학위를 취득했습니다. 컴퓨터 소프트웨어 엔지니어링, 머신 러닝, 금융 분야에서 10년의 경력을 쌓았습니다. 딥 러닝의 최신 발전에 대해 읽고 이를 기업 문제 해결에 적용하는 것을 좋아합니다.

댓글