
GPU Gems 3
GPU Gems 3 is now available for free online!
The CD content, including demos and content, is available on the web and for download.
You can also subscribe to our Developer News Feed to get notifications of new material on the site.
Chapter 39. Parallel Prefix Sum (Scan) with CUDA
Mark Harris
NVIDIA Corporation
Shubhabrata Sengupta
University of California, Davis
John D. Owens
University of California, Davis
39.1 Introduction
A simple and common parallel algorithm building block is the all-prefix-sums operation. In this chapter, we define and illustrate the operation, and we discuss in detail its efficient implementation using NVIDIA CUDA. Blelloch (1990) describes all-prefix-sums as a good example of a computation that seems inherently sequential, but for which there is an efficient parallel algorithm. He defines the all-prefix-sums operation as follows:
The all-prefix-sums operation takes a binary associative operator
with identity I, and an array of n elements
[a 0, a 1,..., a n–1],
and returns the array
[I, a 0, (a 0
a 1),..., (a 0
a 1
...
a n–2)]
For example, if
is addition, then the all-prefix-sums operation on the array
|
[3 1 7 0 4 1 6 3] |
would return
|
[0 3 4 11 11 15 16 22]. |
The all-prefix-sums operation on an array of data is commonly known as scan. We use this simpler terminology (which comes from the APL programming language [Iverson 1962]) for the remainder of this chapter. The scan just defined is an exclusive scan, because each element j of the result is the sum of all elements up to but not including j in the input array. In an inclusive scan, all elements including j are summed. An exclusive scan can be generated from an inclusive scan by shifting the resulting array right by one element and inserting the identity. Likewise, an inclusive scan can be generated from an exclusive scan by shifting the resulting array left and inserting at the end the sum of the last element of the scan and the last element of the input array (Blelloch 1990). For the remainder of this chapter, we focus on the implementation of exclusive scan and refer to it simply as "scan" unless otherwise specified.
There are many uses for scan, including, but not limited to, sorting, lexical analysis, string comparison, polynomial evaluation, stream compaction, and building histograms and data structures (graphs, trees, and so on) in parallel. For example applications, we refer the reader to the survey by Blelloch (1990). In this chapter, we cover summed-area tables (used for variable-width image filtering), stream compaction, and radix sort.
In general, all-prefix-sums can be used to convert certain sequential computations into equivalent, but parallel, computations, as shown in Figure 39-1.
Table 39-1. A Sequential Computation and Its Parallel Equivalent
|
Sequential |
Parallel |
|
|
39.1.1 Sequential Scan and Work Efficiency
Implementing a sequential version of scan (that could be run in a single thread on a CPU, for example) is trivial. We simply loop over all the elements in the input array and add the value of the previous element of the input array to the sum computed for the previous element of the output array, and write the sum to the current element of the output array.
out[0] := 0 for k := 1 to n do
out[k] := in[k-1] + out[k-1]This code performs exactly n adds for an array of length n; this is the minimum number of adds required to produce the scanned array. When we develop our parallel version of scan, we would like it to be work-efficient. A parallel computation is work-efficient if it does asymptotically no more work (add operations, in this case) than the sequential version. In other words the two implementations should have the same work complexity, O(n).
39.2 Implementation
The sequential scan algorithm is poorly suited to GPUs because it does not take advantage of the GPU's data parallelism. We would like to find a parallel version of scan that can utilize the parallel processors of a GPU to speed up its computation. In this section we work through the CUDA implementation of a parallel scan algorithm. We start by introducing a simple but inefficient implementation and then present improvements to both the algorithm and the implementation in CUDA.
39.2.1 A Naive Parallel Scan
The pseudocode in Algorithm 1 shows a first attempt at a parallel scan. This algorithm is based on the scan algorithm presented by Hillis and Steele (1986) and demonstrated for GPUs by Horn (2005). Figure 39-2 illustrates the operation. The problem with Algorithm 1 is apparent if we examine its work complexity. The algorithm performs O(n log2 n) addition operations. Remember that a sequential scan performs O(n) adds. Therefore, this naive implementation is not work-efficient. The factor of log2 n can have a large effect on performance.
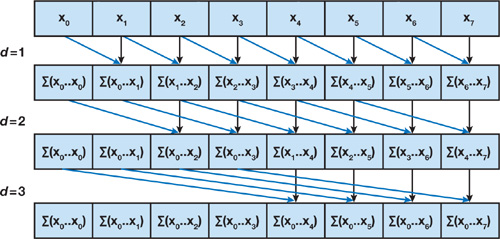
Figure 39-2 The Naive Scan of
Example 1. A Sum Scan Algorithm That Is Not Work-Efficient
1: for d = 1 to log2 n do
2: for all k in parallel do
3: if k
2
d then
4: x[k] = x[k – 2 d-1] + x[k]
Algorithm 1 assumes that there are as many processors as data elements. For large arrays on a GPU running CUDA, this is not usually the case. Instead, the programmer must divide the computation among a number of thread blocks that each scans a portion of the array on a single multiprocessor of the GPU. Even still, the number of processors in a multiprocessor is typically much smaller than the number of threads per block, so the hardware automatically partitions the "for all" statement into small parallel batches (called warps) that are executed sequentially on the multiprocessor. An NVIDIA 8 Series GPU executes warps of 32 threads in parallel. Because not all threads run simultaneously for arrays larger than the warp size, Algorithm 1 will not work, because it performs the scan in place on the array. The results of one warp will be overwritten by threads in another warp.
To solve this problem, we need to double-buffer the array we are scanning using two temporary arrays. Pseudocode for this is given in Algorithm 2, and CUDA C code for the naive scan is given in Listing 39-1. Note that this code will run on only a single thread block of the GPU, and so the size of the arrays it can process is limited (to 512 elements on NVIDIA 8 Series GPUs). Extension of scan to large arrays is discussed in Section 39.2.4.
Example 2. A Double-Buffered Version of the Sum Scan from Algorithm 1
1: for d = 1 to log2 n do
2: for all k in parallel do
3: if k
2
d then
4: x[out][k] = x[in][k – 2 d-1] +
x[in][k]
5: else
6: x[out][k] = x[in][k]
Example 39-1. CUDA C Code for the Naive Scan Algorithm
This version can handle arrays only as large as can be processed by a single thread block running on one multiprocessor of a GPU.
__global__ void scan(float *g_odata, float *g_idata, int n)
{
extern __shared__ float temp[]; // allocated on invocation
int thid = threadIdx.x;
int pout = 0, pin = 1;
// Load input into shared memory.
// This is exclusive scan, so shift right by one
// and set first element to 0
temp[pout * n + thid] = (thid > 0) ? g_idata[thid - 1] : 0;
__syncthreads();
for (int offset = 1; offset < n; offset *= 2)
{
pout = 1 - pout; // swap double buffer indices
pin = 1 - pout;
if (thid > = offset)
temp[pout * n + thid] += temp[pin * n + thid - offset];
else
temp[pout * n + thid] = temp[pin * n + thid];
__syncthreads();
}
g_odata[thid] = temp[pout * n + thid]; // write output
}39.2.2 A Work-Efficient Parallel Scan
Our implementation of scan from Section 39.2.1 would probably perform very badly on large arrays due to its work-inefficiency. We would like to find an algorithm that would approach the efficiency of the sequential algorithm, while still taking advantage of the parallelism in the GPU. Our goal in this section is to develop a work-efficient scan algorithm for CUDA that avoids the extra factor of log2 n work performed by the naive algorithm. This algorithm is based on the one presented by Blelloch (1990). To do this we will use an algorithmic pattern that arises often in parallel computing: balanced trees. The idea is to build a balanced binary tree on the input data and sweep it to and from the root to compute the prefix sum. A binary tree with n leaves has d = log2 n levels, and each level d has 2 d nodes. If we perform one add per node, then we will perform O(n) adds on a single traversal of the tree.
The tree we build is not an actual data structure, but a concept we use to determine what each thread does at each step of the traversal. In this work-efficient scan algorithm, we perform the operations in place on an array in shared memory. The algorithm consists of two phases: the reduce phase (also known as the up-sweep phase) and the down-sweep phase. In the reduce phase, we traverse the tree from leaves to root computing partial sums at internal nodes of the tree, as shown in Figure 39-3. This is also known as a parallel reduction, because after this phase, the root node (the last node in the array) holds the sum of all nodes in the array. Pseudocode for the reduce phase is given in Algorithm 3.

Figure 39-3 An Illustration of the Up-Sweep, or Reduce, Phase of a Work-Efficient Sum Scan Algorithm
Example 3. The Up-Sweep (Reduce) Phase of a Work-Efficient Sum Scan Algorithm (After Blelloch 1990)
1: for d = 0 to log2 n – 1 do
2: for all k = 0 to n – 1 by 2 d+1 in parallel
do
3: x[k + 2 d+1 – 1] = x[k + 2 d – 1]
+ x[k + 2 d +1 – 1]
In the down-sweep phase, we traverse back down the tree from the root, using the partial sums from the reduce phase to build the scan in place on the array. We start by inserting zero at the root of the tree, and on each step, each node at the current level passes its own value to its left child, and the sum of its value and the former value of its left child to its right child. The down-sweep is shown in Figure 39-4, and pseudocode is given in Algorithm 4. CUDA C code for the complete algorithm is given in Listing 39-2. Like the naive scan code in Section 39.2.1, the code in Listing 39-2 will run on only a single thread block. Because it processes two elements per thread, the maximum array size this code can scan is 1,024 elements on an NVIDIA 8 Series GPU. Scans of larger arrays are discussed in Section 39.2.4.
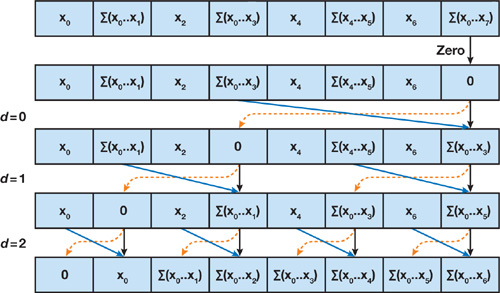
Figure 39-4 An Illustration of the Down-Sweep Phase of the Work-Efficient Parallel Sum Scan Algorithm
Example 4. The Down-Sweep Phase of a Work-Efficient Parallel Sum Scan Algorithm (After Blelloch 1990)
1: x[n – 1]
0
2: for d = log2 n – 1 down to 0 do
3: for all k = 0 to n – 1 by 2 d +1 in parallel
do
4: t = x[k + 2 d – 1]
5: x[k + 2 d – 1] = x[k + 2 d +1 –
1]
6: x[k + 2 d +1 – 1] = t + x[k + 2
d +1 – 1]
The scan algorithm in Algorithm 4 performs O(n) operations (it performs 2 x (n – 1) adds and n – 1 swaps); therefore it is work-efficient and, for large arrays, should perform much better than the naive algorithm from the previous section. Algorithmic efficiency is not enough; we must also use the hardware efficiently. If we examine the operation of this scan on a GPU running CUDA, we will find that it suffers from many shared memory bank conflicts. These hurt the performance of every access to shared memory and significantly affect overall performance. In the next section, we look at some simple modifications we can make to the memory address computations to recover much of that lost performance.
Example 39-2. CUDA C Code for the Work-Efficient Sum Scan of Algorithms 3 and 4.
|
The highlighted blocks are discussed in Section 39.2.3. |
|
|
|
|
A |
|
|
|
|
B |
|
|
|
|
C |
|
|
|
|
D |
|
|
|
|
E |
|
|
39.2.3 Avoiding Bank Conflicts
The scan algorithm of the previous section performs approximately as much work as an optimal sequential algorithm. Despite this work-efficiency, it is not yet efficient on NVIDIA GPU hardware, due to its memory access patterns. As described in the NVIDIA CUDA Programming Guide (NVIDIA 2007), the shared memory exploited by this scan algorithm is made up of multiple banks. When multiple threads in the same warp access the same bank, a bank conflict occurs unless all threads of the warp access the same address within the same 32-bit word. The number of threads that access a single bank is called the degree of the bank conflict. Bank conflicts cause serialization of the multiple accesses to the memory bank, so that a shared memory access with a degree-n bank conflict requires n times as many cycles to process as an access with no conflict. On NVIDIA 8 Series GPUs, which execute 16 threads in parallel in a halfwarp, the worst case is a degree-16 bank conflict.
Binary tree algorithms such as our work-efficient scan double the stride between memory accesses at each level of the tree, simultaneously doubling the number of threads that access the same bank. For deep trees, as we approach the middle levels of the tree, the degree of the bank conflicts increases, and then it decreases again near the root, where the number of active threads decreases (due to the if statement in Listing 39-2). For example, if we are scanning a 512-element array, the shared memory reads and writes in the inner loops of Listing 39-2 experience up to 16-way bank conflicts. This has a significant effect on performance.
Bank conflicts are avoidable in most CUDA computations if care is taken when accessing __shared__ memory arrays. We can avoid most bank conflicts in scan by adding a variable amount of padding to each shared memory array index we compute. Specifically, we add to the index the value of the index divided by the number of shared memory banks. This is demonstrated in Figure 39-5. We start from the work-efficient scan code in Listing 39-2, modifying only the highlighted blocks A through E. To simplify the code changes, we define a macro CONFLICT_FREE_OFFSET, shown in Listing 39-3.
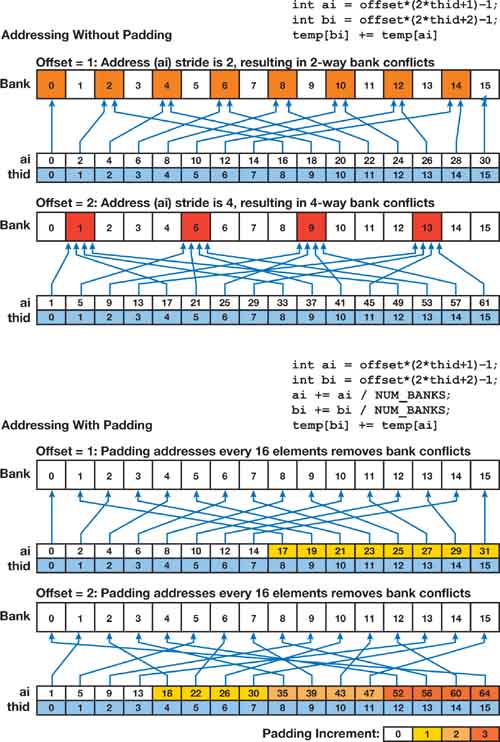
Figure 39-5 Simple Padding Applied to Shared Memory Addresses Can Eliminate High-Degree Bank Conflicts During Tree-Based Algorithms Like Scan
Example 39-3. Macro Used for Computing Bank-Conflict-Free Shared Memory Array Indices
#define NUM_BANKS 16
#define LOG_NUM_BANKS 4
#define CONFLICT_FREE_OFFSET(n)((n) >>
NUM_BANKS + (n) >>
(2 * LOG_NUM_BANKS))The blocks A through E in Listing 39-2 need to be modified using this macro to avoid bank conflicts. Two changes must be made to block A. Each thread loads two array elements from the __global__ array g_idata into the __shared__ array temp. In the original code, each thread loads two adjacent elements, resulting in the interleaved indexing of the shared memory array, incurring two-way bank conflicts. By instead loading two elements from separate halves of the array, we avoid these bank conflicts. Also, to avoid bank conflicts during the tree traversal, we need to add padding to the shared memory array every NUM_BANKS (16) elements. We do this using the macro in Listing 39-3 as shown in Listing 39-4. Note that we store the offsets to the shared memory indices so that we can use them again at the end of the scan, when writing the results back to the output array g_odata in block E.
Example 39-4. Modifications to the Work-Efficient Scan Code to Avoid Shared Memory Bank Conflicts
Block A:
int ai = thid;
int bi = thid + (n / 2);
int bankOffsetA = CONFLICT_FREE_OFFSET(ai) int bankOffsetB =
CONFLICT_FREE_OFFSET(bi) temp[ai + bankOffsetA] =
g_idata[ai] temp[bi + bankOffsetB] = g_idata[bi]Blocks B and D are identical:
int ai = offset * (2 * thid + 1) - 1;
int bi = offset * (2 * thid + 2) - 1;
ai += CONFLICT_FREE_OFFSET(ai) bi += CONFLICT_FREE_OFFSET(bi)Block C:
if (thid == 0)
{
temp[n - 1 + CONFLICT_FREE_OFFSET(n - 1)] = 0;
}Block E:
g_odata[ai] = temp[ai + bankOffsetA];
g_odata[bi] = temp[bi + bankOffsetB];39.2.4 Arrays of Arbitrary Size
The algorithms given in the previous sections scan an array inside a single thread block. This is fine for small arrays, up to twice the maximum number of threads in a block (since each thread loads and processes two elements). On NVIDIA 8 Series GPUs, this limits us to a maximum of 1,024 elements. Also, the array size must be a power of two. In this section, we explain how to extend the algorithm to scan large arrays of arbitrary (non-power-of-two) dimensions. This algorithm is based on the explanation provided by Blelloch (1990).
The basic idea is simple. We divide the large array into blocks that each can be scanned by a single thread block, and then we scan the blocks and write the total sum of each block to another array of block sums. We then scan the block sums, generating an array of block increments that that are added to all elements in their respective blocks. In more detail, let N be the number of elements in the input array, and B be the number of elements processed in a block. We allocate N/B thread blocks of B/2 threads each. (Here we assume that N is a multiple of B, and we extend to arbitrary dimensions in the next paragraph.) A typical choice for B on NVIDIA 8 Series GPUs is 128. We use the scan algorithm of the previous sections to scan each block i independently, storing the resulting scans to sequential locations of the output array. We make one minor modification to the scan algorithm. Before zeroing the last element of block i (the block of code labeled B in Listing 39-2), we store the value (the total sum of block i) to an auxiliary array SUMS. We then scan SUMS in the same manner, writing the result to an array INCR. We then add INCR[i] to all elements of block i using a simple uniform add kernel invoked on N/B thread blocks of B/2 threads each. This is demonstrated in Figure 39-6. For details of the implementation, please see the source code available at http://www.gpgpu.org/scan-gpugems3/.
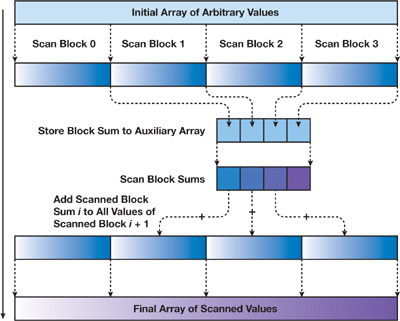
Figure 39-6 Algorithm for Performing a Sum Scan on a Large Array of Values
Handling non-power-of-two dimensions is easy. We simply pad the array out to the next multiple of the block size B. The scan algorithm is not dependent on elements past the end of the array, so we don't have to use a special case for the last block.
39.2.5 Further Optimization and Performance Results
After optimizing shared memory accesses, the main bottlenecks left in the scan code are global memory latency and instruction overhead due to looping and address computation instructions. To better cover the global memory access latency and improve overall efficiency, we need to do more computation per thread. We employ a technique suggested by David Lichterman, which processes eight elements per thread instead of two by loading two float4 elements per thread rather than two float elements (Lichterman 2007). Each thread performs a sequential scan of each float4, stores the first three elements of each scan in registers, and inserts the total sum into the shared memory array. With the partial sums from all threads in shared memory, we perform an identical tree-based scan to the one given in Listing 39-2. Each thread then constructs two float4 values by adding the corresponding scanned element from shared memory to each of the partial sums stored in registers. Finally, the float4 values are written to global memory. This approach, which is more than twice as fast as the code given previously, is a consequence of Brent's Theorem and is a common technique for improving the efficiency of parallel algorithms (Quinn 1994).
To reduce bookkeeping and loop instruction overhead, we unroll the loops in Algorithms 3 and 4. Because our block size is fixed, we can completely unroll these loops, greatly reducing the extra instructions required to traverse the tree in a loop.
Our efforts to create an efficient scan implementation in CUDA have paid off. Performance is up to 20 times faster than a sequential version of scan running on a fast CPU, as shown in the graph in Figure 39-7. Also, thanks to the advantages provided by CUDA, we outperform an optimized OpenGL implementation running on the same GPU by up to a factor of seven. The graph also shows the performance we achieve when we use the naive scan implementation from Section 39.2.1 for each block. Because both the naive scan and the work-efficient scan must be divided across blocks of the same number of threads, the performance of the naive scan is slower by a factor of O(log2 B), where B is the block size, rather than a factor of O(log2 n). Figure 39-8 compares the performance of our best CUDA implementation with versions lacking bankconflict avoidance and loop unrolling.

Figure 39-7 Performance of the Work-Efficient, Bank-Conflict-Free Scan Implemented in CUDA Compared to a Sequential Scan Implemented in C++, and a Work-Efficient Implementation in OpenGL
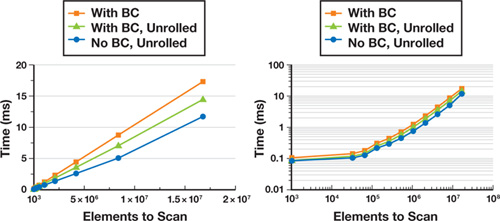
Figure 39-8 Comparison of Performance of the Work-Efficient Scan Implemented in CUDA with Optimizations to Avoid Bank Conflicts and to Unroll Loops
The scan implementation discussed in this chapter, along with example applications, is available online at http://www.gpgpu.org/scan-gpugems3/.
39.2.6 The Advantages of CUDA over the OpenGL Implementation
Prior to the introduction of CUDA, several researchers implemented scan using graphics APIs such as OpenGL and Direct3D (see Section 39.3.4 for more). To demonstrate the advantages CUDA has over these APIs for computations like scan, in this section we briefly describe the work-efficient OpenGL inclusive-scan implementation of Sengupta et al. (2006). Their implementation is a hybrid algorithm that performs a configurable number of reduce steps as shown in Algorithm 5. It then runs the double-buffered version of the sum scan algorithm previously shown in Algorithm 2 on the result of the reduce step. Finally it performs the down-sweep as shown in Algorithm 6.
Example 5. The Reduce Step of the OpenGL Scan Algorithm
1: for d = 1 to log2 n do
2: for all k = 1 to n/2 d – 1 in parallel
do
3: a[d][k] = a[d – 1][2k] + a[d –
1][2k + 1]]
Example 6. The Down-Sweep Step of the OpenGL Scan Algorithm
1: for d = log2 n – 1 down to 0 do
2: for all k = 0 to n/2 d – 1 in parallel
do
3: if i > 0 then
4: if k mod 2
0
then
5: a[d][k] = a[d + 1][k/2]
6: else
7: a[d][i] = a[d + 1][k/2 – 1]
The OpenGL scan computation is implemented using pixel shaders, and each a[d] array is a two-dimensional texture on the GPU. Writing to these arrays is performed using render-to-texture in OpenGL. Thus, each loop iteration in Algorithm 5 and Algorithm 2 requires reading from one texture and writing to another.
The main advantages CUDA has over OpenGL are its on-chip shared memory, thread synchronization functionality, and scatter writes to memory, which are not exposed to OpenGL pixel shaders. CUDA divides the work of a large scan into many blocks, and each block is processed entirely on-chip by a single multiprocessor before any data is written to off-chip memory. In OpenGL, all memory updates are off-chip memory updates. Thus, the bandwidth used by the OpenGL implementation is much higher and therefore performance is lower, as shown previously in Figure 39-7.
39.3 Applications of Scan
As we described in the introduction, scan has a wide variety of applications. In this section, we cover three applications of scan: stream compaction, summed-area tables, and radix sort.
39.3.1 Stream Compaction
Stream compaction is an important primitive in a variety of general-purpose applications, including collision detection and sparse matrix compression. In fact, stream compaction was the focus of most of the previous GPU work on scan (see Section 39.3.4). Stream compaction is the primary method for transforming a heterogeneous vector, with elements of many types, into homogeneous vectors, in which each element has the same type. This is particularly useful with vectors that have some elements that are interesting and many elements that are not interesting. Stream compaction produces a smaller vector with only interesting elements. With this smaller vector, computation is more efficient, because we compute on only interesting elements, and thus transfer costs, particularly between the GPU and CPU, are potentially greatly reduced.
Informally, stream compaction is a filtering operation: from an input vector, it selects a subset of this vector and packs that subset into a dense output vector. Figure 39-9 shows an example. More formally, stream compaction takes an input vector vi and a predicate p, and outputs only those elements in vi for which p(vi ) is true, preserving the ordering of the input elements. Horn (2005) describes this operation in detail.

Figure 39-9 Stream Compaction Example
Stream compaction requires two steps, a scan and a scatter.
- The first step generates a temporary vector where the elements that pass the predicate are set to 1 and the other elements are set to 0. We then scan this temporary vector. For each element that passes the predicate, the result of the scan now contains the destination address for that element in the output vector.
- The second step scatters the input elements to the output vector using the addresses generated by the scan.
Figure 39-10 shows this process in detail.

Figure 39-10 Scan and Scatter
The GPUs on which Horn implemented stream compaction in 2005 did not have scatter capability, so Horn instead substituted a sequence of gather steps to emulate scatter. To compact n elements required log n gather steps, and while these steps could be implemented in one fragment program, this "gather-search" operation was fairly expensive and required more memory operations. The addition of a native scatter in recent GPUs makes stream compaction considerably more efficient. Performance of our stream compaction test is shown in Figure 39-11.
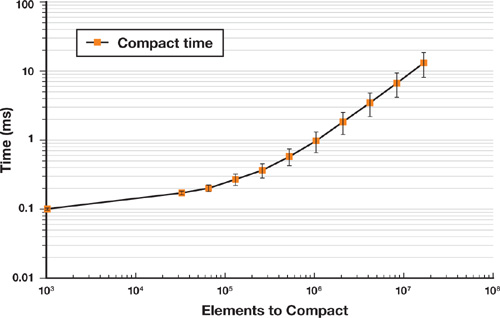
Figure 39-11 Performance of Stream Compaction Implemented in CUDA on an NVIDIA GeForce 8800 GTX GPU
39.3.2 Summed-Area Tables
A summed-area table (SAT) is a two-dimensional table generated from an input image in which each entry in the table stores the sum of all pixels between the entry location and the lower-left corner of the input image. Summed-area tables were introduced by Crow (1984), who showed how they can be used to perform arbitrary-width box filters on the input image. The power of the summed-area table comes from the fact that it can be used to perform filters of different widths at every pixel in the image in constant time per pixel. Hensley et al. (2005) demonstrated the use of fast GPU-generated summed-area tables for interactive rendering of glossy environment reflections and refractions. Their implementation on GPUs used a scan operation equivalent to the naive implementation in Section 39.2.1. A work-efficient implementation in CUDA allows us to achieve higher performance. In this section we describe how summed-area tables can be computed using scans in CUDA, and we demonstrate their use in rendering approximate depth of field.
To compute the summed-area table for a two-dimensional image, we simply apply a sum scan to all rows of the image followed by a sum scan of all columns of the result. To do this efficiently in CUDA, we extend our basic implementation of scan to perform many independent scans in parallel. Thanks to the "grid of thread blocks" semantics provided by CUDA, this is easy; we use a two-dimensional grid of thread blocks, scanning one row of the image with each row of the grid. Modifying scan to support this requires modifying only the computation of the global memory indices from which the data to be scanned in each block are read. Extending scan to also support scanning columns would lead to poor performance, because column scans would require large strides through memory between threads, resulting in noncoalesced memory reads (NVIDIA 2007). Instead, we simply transpose the image after scanning the rows, and then scan the rows of the transposed image.
Generating a box-filtered pixel using a summed-area table requires sampling the summed-area table at the four corners of a rectangular filter region, sur , sul , sll , slr . The filtered result is then
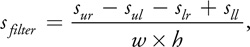
where w and h are the width and height of the filter kernel, and sur is the upper-right corner sample, sll is the lower-left corner sample, and so on (Crow 1977). We can use this technique for variable-width filtering, by varying the locations of the four samples we use to compute each filtered output pixel.
Figure 39-12 shows a simple scene rendered with approximate depth of field, so that objects far from the focal length are blurry, while objects at the focal length are in focus. In the first pass, we render the teapots and generate a summed-area table in CUDA from the rendered image using the technique just described. In the second pass, we render a full-screen quad with a shader that samples the depth buffer from the first pass and uses the depth to compute a blur factor that modulates the width of the filter kernel. This determines the locations of the four samples taken from the summed-area table at each pixel.

Figure 39-12 Approximate Depth of Field Rendered by Using a Summed-Area Table to Apply a Variable-Size Blur to the Image Based on the Depth of Each Pixel
Rather than write a custom scan algorithm to process RGB images, we decided to use our existing code along with a few additional simple kernels. Computing the SAT of an RGB8 input image requires four steps. First we de-interleave the RGB8 image into three separate floating-point arrays (one for each color channel). Next we scan all rows of each array in parallel. Then the arrays must be transposed and all rows scanned again (to scan the columns). This is a total of six scans of width x height elements each. Finally, the three individual summed-area tables are interleaved into the RGB channels of a 32-bit floating-point RGBA image. Note that we don't need to transpose the image again, because we can simply transpose the coordinates we use to look up into it. Table 39-1 shows the time spent on each of these computations for two image sizes.
Table 39-1. Performance of Our Summed-Area Table Implementation on an NVIDIA GeForce 8800 GTX GPU for Two Different Image Sizes
|
Resolution |
(De)interleave (ms) |
Transpose (ms) |
6 Scans (ms) |
Total (ms) |
|
512x512 |
0.44 |
0.23 |
0.97 |
1.64 |
|
1024x1024 |
0.96 |
0.84 |
1.70 |
3.50 |
39.3.3 Radix Sort
Previous GPU-based sorting routines have primarily used variants of bitonic sort (Govindaraju et al. 2006, Greß and Zachmann 2006), an efficient, oblivious sorting algorithm for parallel processors. The scan primitive can be used as a building block for another efficient sorting algorithm on the GPU, radix sort.
Our implementation first uses radix sort to sort individual chunks of the input array. Chunks are sorted in parallel by multiple thread blocks. Chunks are as large as can fit into the shared memory of a single multiprocessor on the GPU. After sorting the chunks, we use a parallel bitonic merge to combine pairs of chunks into one. This merge is repeated until a single sorted array is produced.
Step 1: Radix Sort Chunks
Radix sort is particularly well suited for small sort keys, such as small integers, that can be expressed with a small number of bits. At a high level, radix sort works as follows. We begin by considering one bit from each key, starting with the least-significant bit. Using this bit, we partition the keys so that all keys with a 0 in that bit are placed before all keys with a 1 in that bit, otherwise keeping the keys in their original order. See Figure 39-13. We then move to the next least-significant bit and repeat the process.
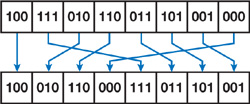
Figure 39-13 Radix Sort
Thus for k-bit keys, radix sort requires k steps. Our implementation requires one scan per step.
The fundamental primitive we use to implement each step of radix sort is the split primitive. The input to split is a list of sort keys and their bit value b of interest on this step, either a true or false. The output is a new list of sort keys, with all false sort keys packed before all true sort keys.
We implement split on the GPU in the following way, as shown in Figure 39-14.
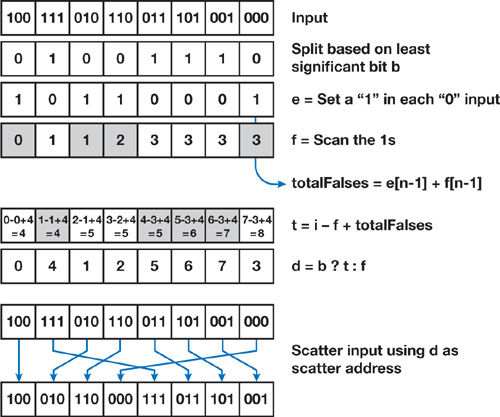
Figure 39-14 The Operation Requires a Single Scan and Runs in Linear Time with the Number of Input Elements
- In a temporary buffer in shared memory, we set a 1 for all false sort keys (b = 0) and a 0 for all true sort keys.
- We then scan this buffer. This is the enumerate operation; each false sort key now contains its destination address in the scan output, which we will call f. These first two steps are equivalent to a stream compaction operation on all false sort keys.
- The last element in the scan's output now contains the total number of false sort keys. [1] We write this value to a shared variable, totalFalses.
- Now we compute the destination address for the true sort keys. For a sort key at index i, this address is t = i - f + totalFalses. We then select between t and f depending on the value of b to get the destination address d of each fragment.
- Finally, we scatter the original sort keys to destination address d. The scatter pattern is a perfect permutation of the input, so we see no write conflicts with this scatter.
With split, we can easily implement radix sort. We begin by loading a block-size chunk of input from global memory into shared memory. We then initialize our current bit to the least-significant bit of the key, split based on the key, check if the output is sorted, and if not shift the current bit left by one and iterate again. When we are done, we copy the sorted data back to global memory. With large inputs, each chunk is mapped to a thread block and runs in parallel with the other chunks.
Step 2: Merge Sorted Chunks
After each block-size chunk is sorted, we use a recursive merge sort to combine two sorted chunks into one sorted chunk. If we have b sorted chunks of size n, we require log2 b steps of merge to get one final sorted output at the end. On the first step, we perform b/2 merges in parallel, each on two n-element sorted streams of input and producing 2n sorted elements of output. On the next step, we do b/4 merges in parallel, each on two 2n-element sorted streams of input and producing 4n sorted elements of output, and so on.
Our merge kernel must therefore operate on two inputs of arbitrary length located in GPU main memory. At a high level, our implementation keeps two buffers in shared memory, one for each input, and uses a parallel bitonic sort to merge the smallest elements from each buffer. It then refills the buffers from main memory if necessary, and repeats until both inputs are exhausted. All reads from global memory into shared memory and all writes to global memory are coherent and blocked; we also guarantee that each input element is read only once from global memory and each output element is written only once.
In our merge kernel, we run p threads in parallel. The most interesting part of our implementation is the computation and sorting of the p smallest elements from two sorted sequences in the input buffers. Figure 39-15 shows this process. For p elements, the output of the pairwise parallel comparison between the two sorted sequences is bitonic and can thus be efficiently sorted with log2 p parallel operations.

Figure 39-15 Merging Two Sorted Subsequences into One Sorted Sequence Is an Efficient Operation
39.3.4 Previous Work
Scan was first proposed in the mid-1950s by Iverson as part of the APL programming language (Iverson 1962). Blelloch was one of the primary researchers to develop efficient algorithms using the scan primitive (Blelloch 1990), including the scan-based radix sort described in this chapter (Blelloch 1989).
On the GPU, the first published scan work was Horn's 2005 implementation (Horn 2005). Horn's scan was used as a building block for a nonuniform stream compaction operation, which was then used in a collision-detection application. Horn's scan implementation had O(n log n) work complexity. Hensley et al. (2005) used scan for summed-area-table generation later that year, improving the overall efficiency of Horn's implementation by pruning unnecessary work. Like Horn's, however, the overall work complexity of Hensley et al.'s technique was also O(n log n).
The first published O(n) implementation of scan on the GPU was that of Sengupta et al. (2006), also used for stream compaction. They showed that a hybrid work-efficient (O(n) operations with 2n steps) and step-efficient (O(n log n) operations with n steps) implementation had the best performance on GPUs such as NVIDIA's GeForce 7 Series. Sengupta et al.'s implementation was used in a hierarchical shadow map algorithm to compact a stream of shadow pages, some of which required refinement and some of which did not, into a stream of only the shadow pages that required refinement. Later that year, Greß et al. (2006) also presented an O(n) scan implementation for stream compaction in the context of a GPU-based collision detection application. Unlike previous GPU-based 1D scan implementations, Greß et al.'s application required a 2D stream reduction, which resulted in fewer steps overall. Greß et al. also used their scan implementation for stream compaction, in this case computing a stream of valid overlapping pairs of colliding elements from a larger stream of potentially overlapping pairs of colliding elements.
39.4 Conclusion
The scan operation is a simple and powerful parallel primitive with a broad range of applications. In this chapter we have explained an efficient implementation of scan using CUDA, which achieves a significant speedup compared to a sequential implementation on a fast CPU, and compared to a parallel implementation in OpenGL on the same GPU. Due to the increasing power of commodity parallel processors such as GPUs, we expect to see data-parallel algorithms such as scan to increase in importance over the coming years.
39.5 References
Blelloch, Guy E. 1989. "Scans as Primitive Parallel Operations." IEEE Transactions on Computers 38(11), pp. 1526–1538.
Blelloch, Guy E. 1990. "Prefix Sums and Their Applications." Technical Report CMU-CS-90-190, School of Computer Science, Carnegie Mellon University.
Crow, Franklin. 1984. "Summed-Area Tables for Texture Mapping." In Computer Graphics (Proceedings of SIGGRAPH 1984) 18(3), pp. 207–212.
Govindaraju, Naga K., Jim Gray, Ritesh Kumar, and Dinesh Manocha. 2006. "GPUTeraSort: High Performance Graphics Coprocessor Sorting for Large Database Management." In Proceedings of the 2006 ACM SIGMOD International Conference on Management of Data, pp. 325–336.
Greß, Alexander, and Gabriel Zachmann. 2006. "GPU-ABiSort: Optimal Parallel Sorting on Stream Architectures." In Proceedings of the 20th IEEE International Parallel and Distributed Processing Symposium.
Greß, Alexander, Michael Guthe, and Reinhard Klein. 2006. "GPU-Based Collision Detection for Deformable Parameterized Surfaces." Computer Graphics Forum 25(3), pp. 497–506.
Hensley, Justin, Thorsten Scheuermann, Greg Coombe, Montek Singh, and Anselmo Lastra. 2005. "Fast Summed-Area Table Generation and Its Applications." Computer Graphics Forum 24(3), pp. 547–555.
Hillis, W. Daniel, and Guy L. Steele, Jr. 1986. "Data Parallel Algorithms." Communications of the ACM 29(12), pp. 1170–1183.
Horn, Daniel. 2005. "Stream Reduction Operations for GPGPU Applications." In GPU Gems 2, edited by Matt Pharr, pp. 573–589. Addison-Wesley.
Iverson, Kenneth E. 1962. A Programming Language. Wiley.
Lichterman, David. 2007. Course project for UIUC ECE 498 AL: Programming Massively Parallel Processors. Wen-Mei Hwu and David Kirk, instructors. http://courses.ece.uiuc.edu/ece498/al/.
NVIDIA Corporation. 2007. NVIDIA CUDA Compute Unified Device Architecture Programming Guide. Version 0.8.1.
Quinn, Michael J. 1994. Parallel Computing: Theory and Practice, 2nd ed. McGraw-Hill.
Sengupta, Shubhabrata, Aaron E. Lefohn, and John D. Owens. 2006. "A Work-Efficient Step-Efficient Prefix Sum Algorithm." In Proceedings of the Workshop on Edge Computing Using New Commodity Architectures, pp. D-26–27.
- Contributors
- Foreword
- Part I: Geometry
-
- Chapter 1. Generating Complex Procedural Terrains Using the GPU
- Chapter 2. Animated Crowd Rendering
- Chapter 3. DirectX 10 Blend Shapes: Breaking the Limits
- Chapter 4. Next-Generation SpeedTree Rendering
- Chapter 5. Generic Adaptive Mesh Refinement
- Chapter 6. GPU-Generated Procedural Wind Animations for Trees
- Chapter 7. Point-Based Visualization of Metaballs on a GPU
- Part II: Light and Shadows
-
- Chapter 8. Summed-Area Variance Shadow Maps
- Chapter 9. Interactive Cinematic Relighting with Global Illumination
- Chapter 10. Parallel-Split Shadow Maps on Programmable GPUs
- Chapter 11. Efficient and Robust Shadow Volumes Using Hierarchical Occlusion Culling and Geometry Shaders
- Chapter 12. High-Quality Ambient Occlusion
- Chapter 13. Volumetric Light Scattering as a Post-Process
- Part III: Rendering
-
- Chapter 14. Advanced Techniques for Realistic Real-Time Skin Rendering
- Chapter 15. Playable Universal Capture
- Chapter 16. Vegetation Procedural Animation and Shading in Crysis
- Chapter 17. Robust Multiple Specular Reflections and Refractions
- Chapter 18. Relaxed Cone Stepping for Relief Mapping
- Chapter 19. Deferred Shading in Tabula Rasa
- Chapter 20. GPU-Based Importance Sampling
- Part IV: Image Effects
-
- Chapter 21. True Impostors
- Chapter 22. Baking Normal Maps on the GPU
- Chapter 23. High-Speed, Off-Screen Particles
- Chapter 24. The Importance of Being Linear
- Chapter 25. Rendering Vector Art on the GPU
- Chapter 26. Object Detection by Color: Using the GPU for Real-Time Video Image Processing
- Chapter 27. Motion Blur as a Post-Processing Effect
- Chapter 28. Practical Post-Process Depth of Field
- Part V: Physics Simulation
-
- Chapter 29. Real-Time Rigid Body Simulation on GPUs
- Chapter 30. Real-Time Simulation and Rendering of 3D Fluids
- Chapter 31. Fast N-Body Simulation with CUDA
- Chapter 32. Broad-Phase Collision Detection with CUDA
- Chapter 33. LCP Algorithms for Collision Detection Using CUDA
- Chapter 34. Signed Distance Fields Using Single-Pass GPU Scan Conversion of Tetrahedra
- Chapter 35. Fast Virus Signature Matching on the GPU
- Part VI: GPU Computing
-
- Chapter 36. AES Encryption and Decryption on the GPU
- Chapter 37. Efficient Random Number Generation and Application Using CUDA
- Chapter 38. Imaging Earth's Subsurface Using CUDA
- Chapter 39. Parallel Prefix Sum (Scan) with CUDA
- Chapter 40. Incremental Computation of the Gaussian
- Chapter 41. Using the Geometry Shader for Compact and Variable-Length GPU Feedback
- Preface