
GPU Gems 3
GPU Gems 3 is now available for free online!
The CD content, including demos and content, is available on the web and for download.
You can also subscribe to our Developer News Feed to get notifications of new material on the site.
Chapter 15. Playable Universal Capture
George Borshukov
Electronic Arts
Jefferson Montgomery
Electronic Arts
John Hable
Electronic Arts
In this chapter, we discuss a real-time implementation of Universal Capture, abbreviated UCap. The technique has progressed from its noninteractive film applications (in The Matrix movies) through real-time playback (E3 2005 Fight Night Round 3 Concept Demo) to fully interactive (E3 2006 Tiger Woods demo), ultimately being used for animating high-fidelity facial performances in the video game titles Tiger Woods PGA Tour 07 and Need for Speed: Carbon. Based on what we learned from those projects, the system described here is what we believe is the best trade-off that we would advocate for future games and interactive applications.
15.1 Introduction
Digital reproduction of realistic, animated faces is a hard problem for two main reasons:
- There are a vast number of factors involved in reproducing realistic facial animation. If one considers the color of a single pixel, there is near-infinite complexity: the bone structure of the face, blood vessels, muscles, and fat (and their dynamic constriction, excitation, and density); the structure and condition of the layers of skin, makeup, sweat, oil, and dirt affecting reflections and refractions, and so on and so on.
- Despite the subtle nature of some of these factors, many if not all are extremely important because human observers are ultimate experts at watching faces. This is perhaps best described using the Uncanny Valley hypothesis originally posited about humans' response to robots by Dr. Moshiro Mori (Mori 1982). In a nutshell, the Uncanny Valley describes the steep descent toward an unintentionally creepy appearance as the level of realism increases.
The implication of these two factors makes it extremely difficult for an animator or a computer simulation to achieve genuinely realistic results. We simply don't have sufficient models for the important characteristics and subtle dynamics of facial expressions. That is why the techniques in this chapter are based on a philosophy of performance capture. Essentially, we let real-world physics handle the complexity and merely try to capture and reproduce the end result (as pixel values on the face).
Most faces in video games use a diffuse map (which is painted or derived from a photograph) on skinned geometry that is captured through motion capture (a.k.a. mocap). We show how to use three high-resolution video cameras to create an animated diffuse map. This diffuse map captures details that are virtually impossible to animate by hand, including subtle eyebrow movements, subtle lighting changes and self-shadowing effects, stretching of the lips, and wrinkles that move around. We then compress the textures using a variant of principal component analysis (PCA) and entropy-encode both the animated PCA weights and geometry. The textures are then decompressed in a pixel shader on the GPU.
The techniques we present are a direct attempt to avoid the Uncanny Valley in the most challenging applications of all for digital humans: those requiring real-time interactivity. Ultimately, we hope that our collection of techniques will help human characters in video games and other real-time applications to approach the believability and emotional impact offered by their film counterparts.
15.2 The Data Acquisition Pipeline
We have developed a more robust production-level version of the Universal Capture system (Borshukov et al. 2003). To guarantee robustness, we deploy a state-of-the-art facial motion capture system consisting of eight infrared cameras plus three synchronized, high-definition, color cameras framed on the actor's face in an ambient lighting setup. Around 70 small retroreflective markers are placed on the actor's face. The reconstructed 3D motion path of the face markers is then used as the direct source of deformation for the static scanned and surfaced head geometry. We achieve the deformation with a facial bone rig. The number of bones is equal to the number of markers on the face. Figure 15-1 illustrates the process. This deformation approach achieves excellent results in accurately reconstructing the facial shape and motion in all areas of the face—except for the interior contour of the lips, because obviously we cannot place markers there. We solve the lip contour problem with a small set of additional bones that control the lip interior and are quickly keyed by an animator using the background images as a reference. See Figure 15-2. Once we have achieved successful reconstruction of the facial deformations, we can re-project and blend in UV space the input image sequences from each camera for every frame to produce animated diffuse texture maps. The presence of facial markers is not a problem, as our motion capture system needs retroreflective markers only 1.5 mm in diameter, which can easily be keyed out and removed in the final textures, as shown in Figure 15-3. Figure 15-4 shows the final results.
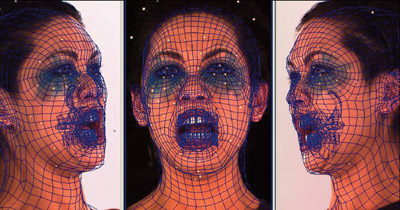
Figure 15-1 Images from All Three of the Camera Views
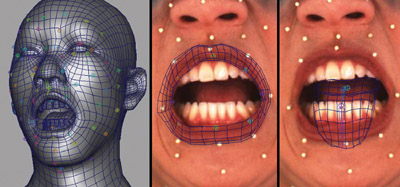
Figure 15-2 Mocap Markers, Lips, and Tongue Are Tracked

Figure 15-3 The Three Camera Views Are Merged and the Markers Are Removed to Create the Final Animated Diffuse Textures
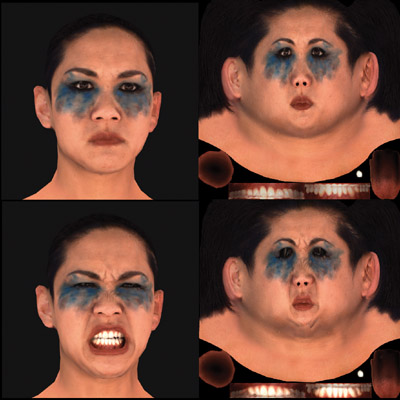
Figure 15-4 The Final Unshaded "Leanne" Character
Our technique enables a straightforward solution to good dynamic lighting of the face: the performances are captured in ambient lighting and a high-detail normal map extracted from a head scan or constructed by an artist can be used for lighting and shading. [1] We treat the diffuse color textures captured by our system as diffuse albedo maps that already contain baked-in ambient occlusion. Subsurface scattering approximation is crucial for close-ups of realistic skin, and we recommend use of the texture space diffusion approach suggested by Borshukov and Lewis 2003 with its most recent real-time implementation by d'Eon 2007. For specular reflectance, we rely on the highly detailed normal map in combination with specular intensity and roughness maps perturbing an analytical model based on findings of Weyrich et al. 2006.
15.3 Compression and Decompression of the Animated Textures
The compression scheme we will use is based on a very simple assumption that can be demonstrated by considering the two-dimensional data set shown in Figure 15-5. We assume in this case that the variance along the x axis is more important than the variance along y. If it is sufficiently more important (enough to disregard the deltas in y as noise), then we can project the data onto this one important dimension and store it in half of the size.
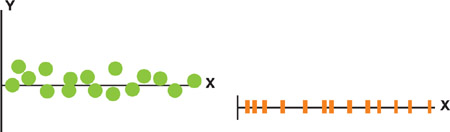
Figure 15-5 A 2D Data Set Demonstrating Our Assumption about Variance
It turns out that for animated facial textures, a large number of dimensions can be deemed unimportant just as y was, and a reasonable compression ratio can be achieved. Further, decompression of this representation involves a simple algorithm that is particularly amenable to parallel implementation on a GPU.
15.3.1 Principal Component Analysis
Animated facial textures are not simple two-dimensional data sets, so we need a technique such as principal component analysis to help us determine which multidimensional axes are the most important. These axes, which are called principal components, are orthogonal and are aligned with the directions of maximal variance, as shown in Figure 15-6. The way that PCA determines these components is by assuming that each data point represents a sample from a multivariate normal distribution. [2] This means that the entire set can be parameterized by a mean vector and a covariance matrix; finding the directions of maximal variance is equivalent to finding a projection that diagonalizes the covariance matrix. For animated facial textures, such an assumption is not entirely dubious, primarily because features are spatially stationary in the UV representation.
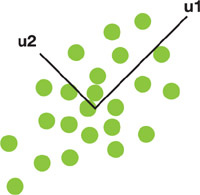
Figure 15-6 A Distribution of Data Points Showing Two Principal Components
The first step in this analysis is to map the texture data into a matrix where rows represent random variables and columns represent samples from a multivariate normal distribution. As shown in Figure 15-7, we treat each texture frame as three samples (corresponding to the red, green, and blue channels) drawn from the same distribution. While this may seem like a strange choice, we have found that this structure allows us to capitalize on correlations between the color channels and ultimately enables better compression.
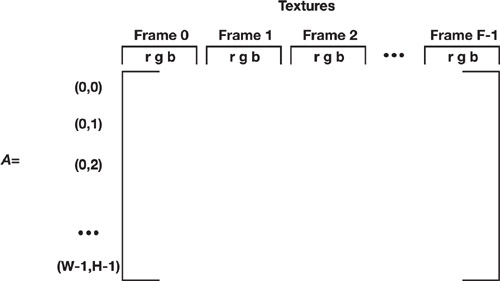
Figure 15-7 The Matrix Structure of an Animated Diffuse Map Used in Principal Component Analysis
The next step is to compute the underlying parameters of the distribution. First, we compute the mean vector and subtract it from each column of the data matrix, thereby "centering" the data:
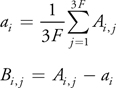
We then want to compute the covariance matrix of B and diagonalize it. Both of these steps can be performed at once by determining the singular value decomposition (SVD) of the matrix B:
|
B =
U |
The result of this operation is the following:
- The columns of U contain the principal components of A. Each component is a vector of length W x H, and there are rank(B) of them.
-
is a diagonal matrix whose values are a direct measure of the corresponding component's importance.
- The rows of V are weights that describe how to linearly combine the principal components to reconstruct B.
15.3.2 Compression
After PCA, the components that make up the animation are ranked in terms of importance. The relative importance
of each component can be viewed by plotting the diagonal terms of
,
as was done in Figure 15-8. Although for this data
very few components are truly redundant (indicated by an importance of zero), a large number of them contribute
relatively little to the final result.
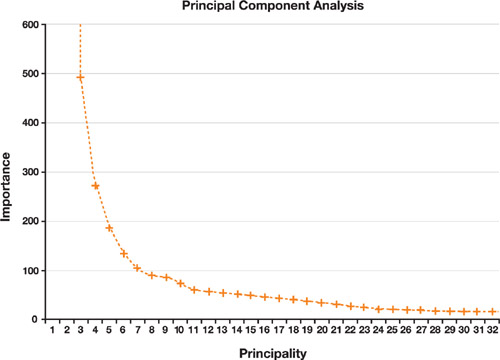
Figure 15-8 The First 32 Diagonal Values of
for a Particular Leanne Performance
The idea behind PCA compression is to simply exclude those components that contribute the least. This effectively projects the data onto a lower-dimensional representation, thereby compressing the data set. For our Leanne example, we may choose to use only 16 out of the 10,644 components to represent the animation. Although this is a significant amount of compression, it is important to note that it introduces errors, because the excluded components (all but the top row in Figure 15-9) contain relevant structure that is lost.
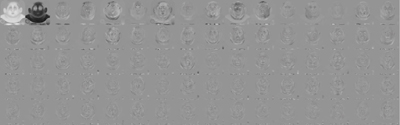
Figure 15-9 The 80 Most Principal Components of a Leanne Performance Ordered from Left to Right, Top to Bottom
15.3.3 Decompression
The decompression algorithm is simply the matrix arithmetic required to recombine U,
,
V, and a into A based on the equations in Section 15.3.1. For
notational simplicity, consider the matrices L and R such that
A = LR. See Figure
15-10.
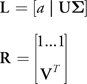
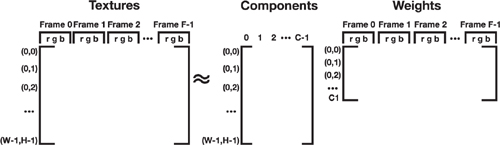
Figure 15-10 Matrix Dimensions for the Decompression Algorithm, =
To reconstruct frame f from this representation using C components, the following equations are used (as shown in Figure 15-11).
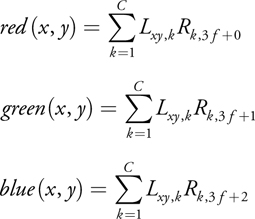

Figure 15-11 Graphical Representation of the Frame Decompression Algorithm
PCA ensures that this is the optimal linear combination of any C components. Further, because the decompression algorithm is simply a matrix-matrix multiplication, it can be easily implemented by a GPU shader. Listing 15-1, where the C columns of L are stored in textures and the frame's corresponding three columns of R are passed in as uniform parameters, shows just such a shader.
Example 15-1. GPU Implementation of PCA Decompression of 16 Components
The first 16 columns of U are packed into four textures by translating the values into the range [0, 255].
// Decompress a pixel color using 16 components.
float4 PcaDecompress16(uniform float2 uv, uniform sampler2D componentTexture[4],
uniform float4 rFrameWeights[4],
uniform float4 gFrameWeights[4],
uniform float4 bFrameWeights[4])
{
// components[0] holds the first four components; the values must be
// mapped from [0, 1] to [-1, 1], which is the original range of the
// columns of U
float4 components[4];
components[0] = 2 * tex2D(componentTexture[0], uv.xy) - 1;
components[1] = 2 * tex2D(componentTexture[1], uv.xy) - 1;
components[2] = 2 * tex2D(componentTexture[2], uv.xy) - 1;
components[3] = 2 * tex2D(componentTexture[3], uv.xy) - 1;
// Matrix multiply LxR
float4 color;
color.r = dot(components[0], rFrameWeights[0]) +
dot(components[1], rFrameWeights[1]) +
dot(components[2], rFrameWeights[2]) +
dot(components[3], rFrameWeights[3]);
color.g = dot(components[0], gFrameWeights[0]) +
dot(components[1], gFrameWeights[1]) +
dot(components[2], gFrameWeights[2]) +
dot(components[3], gFrameWeights[3]);
color.b = dot(components[0], bFrameWeights[0]) +
dot(components[1], bFrameWeights[1]) +
dot(components[2], bFrameWeights[2]) +
dot(components[3], bFrameWeights[3]);
color.a = 1.0;
return color;
}15.3.4 Variable PCA
The optimality of PCA is based on the preceding assumptions as well as one that meansquared error is an appropriate measure of quality. This is unfortunately not the case for animated facial diffuse maps, where certain pixels have a higher qualitative importance and therefore should suffer less error. The prototypical example is to compare the eyes with the back of the head—although PCA treats each pixel with equivalent importance, a human observer would be more offended by an error in the eyes than in the hair.
We have devised a technique designed to retain the benefits of PCA while relaxing the orthonormal constraint on U, allowing us to be selective about how much data is retained per pixel. With variable PCA, the standard compression step of retaining only the most-principal C components is replaced with a step in which each pixel is assigned a distinct number of most-principal components. Pixel i gets C i components and pixel j gets C j components, but C i does not necessarily equal C j . This way, we can affect the quality of the image on a pixel-by-pixel basis. For example, hair pixels can use 4 components while eye pixels can use 88.
The component assignment can also be performed on a region-by-region basis, which greatly simplifies the decompression algorithm because the handling of each region can be hard-coded. For example, Figure 15-12 shows one particular region specification along with the number of components used in each region. This particular specification allows the use of 88 components in the eye regions and greatly increases perceived quality while still fitting all of the component data into the same texture size used by the standard 16-component PCA representation.
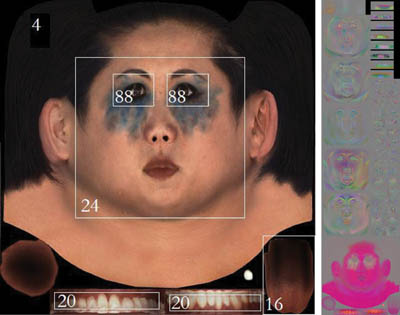
Figure 15-12 A Region Specification
15.3.5 Practical Considerations
As the length of an animation increases, the matrix A can easily become too large to fit into memory on many machines. There are various solutions to this problem, either by using an out-of-core SVD implementation that is able to operate on subsets of A at a time, or by simply analyzing a subset of the frames and then projecting the unanalyzed frames into the basis obtained.
Final quality, memory usage, and required computation are factors that need to be balanced on a per-application basis. Should further compression be required, it can be achieved by compressing the PCA weight streams using a technique such as entropy encoding. The loss in quality is typically worth the memory savings. The weight decompression does require CPU time, but the CPU cost is relatively small because each frame's PCA weights and bone animation involve only a few hundred floats. Ultimately, the majority of the decompression cost is performed on the GPU in the pixel shader, which is beneficial because only visible pixels need be decompressed.
The achieved data size and decompression speed allow us to render multiple, highquality character performances simultaneously in real time. For example, using the variable PCA region layout in Figure 15-12, the components for a 512x512 texture can be stored inside a 512x2048 texture requiring 4MB of RAM. The largest performance set we tested containing 5,672 frames required 803KB of PCA weights and 601KB of bone animation [3] —a total size less than 6MB. Figure 15-13 shows the resulting performance.
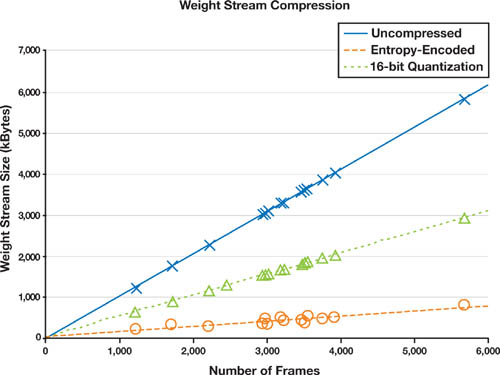
Figure 15-13 Typical Compression Ratios for PCA Weight Streams
15.4 Sequencing Performances
Not only does this compression technique allow us to encode large libraries of performance clips, but it also allows random access as well as any linear operation to be done in compressed space. For example, blending the PCA weights representing two frames prior to decompression is equivalent to pixel-wise blending of the entire frames but requires much less computation. We use these advantages to sequence multiple performances dynamically, blending across transitions.
The fact that this technique preserves the captured subtlety and variety of a performance allows us to apply motion graphs to facial animation. Using motion graphs (a.k.a move trees) is a common practice in video game development, and they have been applied successfully to produce rich and realistic body movement from both captured and hand-animated clips. To apply the motion graph approach to facial animation, a library of facial expression clips, fundamental to a certain context, are captured. A motion graph is designed to connect the expressions, and the graph can be traversed, rendering the clips and interpolating both textures and geometry across the transitions. Performances can be triggered either by an AI subsystem or directly by the user through a game controller.
15.5 Conclusion
We have demonstrated a powerful approach for realistic human character animation and rendering. Figures 15-14 through 15-17 show some examples of the results. Listing 15-2 has the code for the shader. Our approach is based on the application of PCA for compression and GPU decompression of animated diffuse texture maps acquired by a state-of-the-art facial performance capture system. The results have been applied and tested in high-fidelity real-time prototypes as well as in real video game production.

Figure 15-14 The Final Shaded "Leanne" Character

Figure 15-15 A Frame from the E3 2006 Tiger Woods Demo Showing Faithful Reproduction of Tiger's Signature Smile

Figure 15-16 More Frames from the Tiger Woods Demo

Figure 15-17 A Frame from
Example 15-2. The Variable PCA Shader for the Regions from Figure 15-12
struct tPcaTex
{
uniform float faceHeight;
uniform float eyesHeight;
uniform sampler2D Tex0;
uniform float4 TexWeightR[32];
uniform float4 TexWeightG[32];
uniform float4 TexWeightB[32];
};
float PcaDec(float4 weights[], float4 components[], const int num,
const int w_start, const int c_start)
{
int i;
float ret;
ret = 0;
for (int i = 0; i < num; i++)
ret += dot(weights[i + w_start], components[i + c_start]);
return ret;
}
struct UcapWindow
{
float x, y, width, height;
void Set(float f1, float f2, float f3, float f4)
{
x = f1 / 512.0;
y = f2 / 512.0;
width = f3 / 512.0;
height = f4 / 512.0;
}
float2 GetCorner() { return float2(x, y); }
};
bool InWindow(UcapWindow win, float2 uv)
{
if (win.x < uv.x && uv.x < win.x + win.width && win.y < uv.y &&
uv.y < win.y + win.height)
return true;
else
return false;
}
float3 DecompressPcaColor(float2 tex, tPcaTex pcaTex)
{
float4 comp_all[1];
float4 comp_face[5];
float4 comp_eyes[16];
float4 comp_upper_tongue[3];
float4 comp_lower_teeth[4];
float4 comp_upper_teeth[4];
float3 color;
comp_all[0] = tex2D(pcaTex.Tex0, tex.xy * float2(1, .25)) * 2 - 1;
color.r = PcaDec(pcaTex.TexWeightR, comp_all, 1, 0, 0);
color.g = PcaDec(pcaTex.TexWeightG, comp_all, 1, 0, 0);
color.b = PcaDec(pcaTex.TexWeightB, comp_all, 1, 0, 0);
UcapWindow faceWindow, eyesWindow, upperTongueWindow, upperTeethWindow,
lowerTeethWindow;
faceWindow.Set(96, pcaTex.faceHeight, 320, 288);
eyesWindow.Set(160, pcaTex.eyesHeight, 192, 64);
upperTeethWindow.Set(106, 2, 150, 56);
lowerTeethWindow.Set(256, 2, 150, 56);
upperTongueWindow.Set(414, 2, 96, 96);
if (InWindow(faceWindow, tex.xy))
{
for (int i = 0; i < 5; i++)
{
comp_face[i] =
tex2D(pcaTex.Tex0,
((tex.xy - faceWindow.GetCorner()) * float2(1, .25)) +
float2(0, .25 + i * (288.0 / 2048.0))) *
2 -
1;
}
color.r += PcaDec(pcaTex.TexWeightR, comp_face, 5, 1, 0);
color.g += PcaDec(pcaTex.TexWeightG, comp_face, 5, 1, 0);
color.b += PcaDec(pcaTex.TexWeightB, comp_face, 5, 1, 0);
if (InWindow(eyesWindow, tex.xy))
{
for (int i = 0; i < 16; i++)
{
comp_eyes[i] =
tex2D(pcaTex.Tex0,
((tex.xy - eyesWindow.GetCorner()) * float2(1, .25)) +
float2(320.0 / 512.0, .25 + i * (64.0 / 2048.0))) *
2 -
1;
}
color.r += PcaDec(pcaTex.TexWeightR, comp_eyes, 16, 6, 0);
color.g += PcaDec(pcaTex.TexWeightG, comp_eyes, 16, 6, 0);
color.b += PcaDec(pcaTex.TexWeightB, comp_eyes, 16, 6, 0);
}
}
else
{
if (InWindow(upperTeethWindow, tex.xy))
{
for (int i = 0; i < 4; i++)
{
comp_upper_teeth[i] =
tex2D(pcaTex.Tex0,
((tex.xy - upperTeethWindow.GetCorner()) * float2(1, .25)) +
float2(320.0 / 512.0, .75 + i * (128.0 / 2048.0))) *
2 -
1;
}
color.r += PcaDec(pcaTex.TexWeightR, comp_upper_teeth, 4, 1, 0);
color.g += PcaDec(pcaTex.TexWeightG, comp_upper_teeth, 4, 1, 0);
color.b += PcaDec(pcaTex.TexWeightB, comp_upper_teeth, 4, 1, 0);
}
if (InWindow(lowerTeethWindow, tex.xy))
{
for (int i = 0; i < 4; i++)
{
comp_lower_teeth[i] =
tex2D(pcaTex.Tex0,
((tex.xy - lowerTeethWindow.GetCorner()) * float2(1, .25)) +
float2(320.0 / 512.0, .75 + (64 + i * 128.0) / 2048.0)) *
2 -
1;
}
color.r += PcaDec(pcaTex.TexWeightR, comp_lower_teeth, 4, 1, 0);
color.g += PcaDec(pcaTex.TexWeightG, comp_lower_teeth, 4, 1, 0);
color.b += PcaDec(pcaTex.TexWeightB, comp_lower_teeth, 4, 1, 0);
}
if (InWindow(upperTongueWindow, tex.xy))
{
for (int i = 0; i < 3; i++)
{
comp_upper_tongue[i] =
tex2D(pcaTex.Tex0,
((tex.xy - upperTongueWindow.GetCorner()) * float2(1, .25)) +
float2(i * (96 / 512.0), 1952.0 / 2048.0)) *
2 -
1;
}
color.r += PcaDec(pcaTex.TexWeightR, comp_upper_tongue, 3, 1, 0);
color.g += PcaDec(pcaTex.TexWeightG, comp_upper_tongue, 3, 1, 0);
color.b += PcaDec(pcaTex.TexWeightB, comp_upper_tongue, 3, 1, 0);
}
}
color.rgb /= 255;
return color;
}
float4 mainf(PsInput IN, tPcaTex pcaTex) : COLOR
{
float4 out_color;
out_color.rgb = 0;
out_color.rgb = DecompressPcaColor(IN.tex.xy, pcaTex);
out_color.a = 1;
return out_color;
}15.6 References
Borshukov, George, and J. P. Lewis. 2003. "Realistic Human Face Rendering for The Matrix Reloaded." In ACM SIGGRAPH 2003 Sketches and Applications.
Borshukov, George, Dan Piponi, Oystein Larsen, J. P. Lewis, and Christina Tempelaar-Lietz. 2003. "Universal Capture: Image-Based Facial Animation for The Matrix Reloaded." Sketch presented at SIGGRAPH 2003.
d'Eon, Eugene. 2007. "NVIDIA Demo Team Secrets–Advanced Skin Rendering." Presentation at Game Developers Conference 2007. Available online at http://developer.download.nvidia.com/presentations/2007/gdc/Advanced_Skin.pdf.
Mori, M. 1982. The Buddha in the Robot. Tuttle.
Shlens, Jonathon. 2005. "A Tutorial on Principal Component Analysis." Available online at http://www.cs.cmu.edu/~elaw/papers/pca.pdf.
Strang, G. 1998. Introduction to Linear Algebra. Wellesley-Cambridge Press.
Weyrich, Tim, W. Matusik, H. Pfister, B. Bickel, C. Donner, C. Tu, J. McAndless, J. Lee, A. Ngan, H. W. Jensen, and M. Gross. 2006. "Analysis of Human Faces Using a Measurement-Based Skin Reflectance Model." In ACM Transactions on Graphics (Proceedings of SIGGRAPH 2006) 25(3), pp. 1013–1024.
- Contributors
- Foreword
- Part I: Geometry
-
- Chapter 1. Generating Complex Procedural Terrains Using the GPU
- Chapter 2. Animated Crowd Rendering
- Chapter 3. DirectX 10 Blend Shapes: Breaking the Limits
- Chapter 4. Next-Generation SpeedTree Rendering
- Chapter 5. Generic Adaptive Mesh Refinement
- Chapter 6. GPU-Generated Procedural Wind Animations for Trees
- Chapter 7. Point-Based Visualization of Metaballs on a GPU
- Part II: Light and Shadows
-
- Chapter 8. Summed-Area Variance Shadow Maps
- Chapter 9. Interactive Cinematic Relighting with Global Illumination
- Chapter 10. Parallel-Split Shadow Maps on Programmable GPUs
- Chapter 11. Efficient and Robust Shadow Volumes Using Hierarchical Occlusion Culling and Geometry Shaders
- Chapter 12. High-Quality Ambient Occlusion
- Chapter 13. Volumetric Light Scattering as a Post-Process
- Part III: Rendering
-
- Chapter 14. Advanced Techniques for Realistic Real-Time Skin Rendering
- Chapter 15. Playable Universal Capture
- Chapter 16. Vegetation Procedural Animation and Shading in Crysis
- Chapter 17. Robust Multiple Specular Reflections and Refractions
- Chapter 18. Relaxed Cone Stepping for Relief Mapping
- Chapter 19. Deferred Shading in Tabula Rasa
- Chapter 20. GPU-Based Importance Sampling
- Part IV: Image Effects
-
- Chapter 21. True Impostors
- Chapter 22. Baking Normal Maps on the GPU
- Chapter 23. High-Speed, Off-Screen Particles
- Chapter 24. The Importance of Being Linear
- Chapter 25. Rendering Vector Art on the GPU
- Chapter 26. Object Detection by Color: Using the GPU for Real-Time Video Image Processing
- Chapter 27. Motion Blur as a Post-Processing Effect
- Chapter 28. Practical Post-Process Depth of Field
- Part V: Physics Simulation
-
- Chapter 29. Real-Time Rigid Body Simulation on GPUs
- Chapter 30. Real-Time Simulation and Rendering of 3D Fluids
- Chapter 31. Fast N-Body Simulation with CUDA
- Chapter 32. Broad-Phase Collision Detection with CUDA
- Chapter 33. LCP Algorithms for Collision Detection Using CUDA
- Chapter 34. Signed Distance Fields Using Single-Pass GPU Scan Conversion of Tetrahedra
- Chapter 35. Fast Virus Signature Matching on the GPU
- Part VI: GPU Computing
-
- Chapter 36. AES Encryption and Decryption on the GPU
- Chapter 37. Efficient Random Number Generation and Application Using CUDA
- Chapter 38. Imaging Earth's Subsurface Using CUDA
- Chapter 39. Parallel Prefix Sum (Scan) with CUDA
- Chapter 40. Incremental Computation of the Gaussian
- Chapter 41. Using the Geometry Shader for Compact and Variable-Length GPU Feedback
- Preface