Solar storms consist of massive explosions on the Sun that can release the energy of over 2 billion megatons of TNT in the form of solar flares and Coronal Mass Ejections (CMEs). CMEs eject billions of tons of magnetized plasma into space, and while most of them miss Earth entirely, there have been some in the past that would have inflicted great damage on our modern technological society had they hit us. In order to predict the consequences of such potentially disastrous impacts, we require greater understanding of CME initiation and propagation dynamics. Global magnetohydrodynamic (MHD) simulations, driven by observational data are a key component toward this goal.
In this blog post, we describe the steps, stumbles, and ultimate success of implementing multi-GPU acceleration to our state-of-the-art MHD simulation code using OpenACC in a fully portable manner resulting in a single source-code base. We hope sharing our experience helps other developers decide if using OpenACC to accelerate their legacy code is right for them.
The MAS Code
The Magnetohydrodynamic Algorithm outside a Sphere (MAS) code has been in development for over 15 years and used extensively in Solar Physics research, including the simulation of CMEs and the solar wind. For example, it was used to predict what the corona would look like during the August 21st, 2017 total solar eclipse [1-3]. MAS solves the thermodynamic resistive magnetohydrodynamics equations on a non-uniform spherical grid. Consisting of over 50,000 lines of FORTRAN code, MAS is parallelized using MPI, allowing it to run on thousands of CPUs.
Why GPUs?
Porting MAS to GPUs would allow us to run multiple small-to-medium sized simulations on an in-house multi-GPU server, greatly benefiting development and parameter studies of real events. In addition, the largest simulations take up a huge portion of our HPC allocations. Having the code run on multiple GPU nodes would enable us to decrease the time-to-solution using the same number of nodes or reduce the total allocation usage, or both.
Why OpenACC?
Re-writing large sections of the MAS code for GPUs using low-level APIs such as CUDA or OpenCL is not feasible due to  portability and development requirements of the domain experts. OpenACC offers a great solution to these problems, since it is portable in that the code can be run on CPUs, GPUs, and other supported architectures. The resulting accelerated code is also backward-compatible as it can be compiled for running on CPUs using any previously supported compiler by simply ignoring the OpenACC comments. We therefore chose to use OpenACC to add GPU acceleration to MAS.
portability and development requirements of the domain experts. OpenACC offers a great solution to these problems, since it is portable in that the code can be run on CPUs, GPUs, and other supported architectures. The resulting accelerated code is also backward-compatible as it can be compiled for running on CPUs using any previously supported compiler by simply ignoring the OpenACC comments. We therefore chose to use OpenACC to add GPU acceleration to MAS.
Can Your Code be Ported? Where to Start?
Code Styles
The first step in determining if OpenACC is right for your code is to examine it for outdated and/or troublesome styles. Examples include using GOTOs, having deep function call chains within inner loops, the use of old vendor-specific code, and bad memory access patterns. Other code styles, such as heavy use of large multi-level derived types, can also complicate development. If your code contains such styles, you should analyze them and determine if OpenACC will still work, and if not, weigh the development time it would take to clean up the code.
In our case, we were fortunate in that MAS uses clean, modernized FORTRAN 90 code and, for the most part, does not suffer from the above programming style problems. This made it a great candidate for OpenACC implementation. Another helpful feature of MAS is that the MPI parallelism is implemented in a minimized way, where each rank works on a small cube of the grid independently and only interacts with MPI when needed.
Profiling
Next, use a profiler to find the critical performance-heavy portions of the code. These parts of the code should be targeted first to determine if the speedup obtained with OpenACC warrants the full code implementation. If these sections of code can be isolated into a reduced feature run of the code, or separated into test code, all the better.
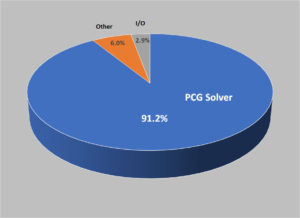
The MAS code can be run with a minimum subset of the full physics model called the Zero-Beta model which neglects thermal pressure and gravity and the evolution is merely driven by magnetic forces. While this is a simplified model, it is still used in production for a variety of simulations such as creating initial CME magnetic field configurations and studying the onset/early evolution of eruptions. The main core algorithms in MAS are the same in the Zero-Beta runs, so our goal for the initial OpenACC implementation presented here is to get MAS running on multiple GPUs for such runs. Profiling the code reveals that the sparse preconditioned conjugate gradient (PCG) solvers used for the velocity equations (semi-implicit predictor-corrector and viscosity) are responsible for over 90% of the run-time on our test problems, as shown in figure 1.
Algorithm Analysis: Vectorization is the Key
When thinking about OpenACC implementations, you should analyze the algorithms your code uses and determine if they are suitable for acceleration. Non-vectorizable algorithms will simply not perform well on a GPU.
allocatable instead of pointer (or at least pointer, contiguous) in order to tell the compiler it’s safe to vectorizeIn MAS, the operations in the PCG solvers consist of sparse matrix-vector products (stencil operations), AXPY operations, and dot products, all of which are vectorizable. This just leaves the preconditioning (PC) step. MAS uses two communication-free preconditioners. The first (PC1) is a point-Jacobi (diagonal scaling), while the second (PC2) is a block-Jacobi using a zero-fill incomplete LU factorization. For MAS runs that have matrix solves requiring many solver iterations (“hard” solves), PC2 runs faster than PC1. However, when the solves only require small numbers of iterations (“easy” solves), using PC1 is faster than PC2. PC2 relies on local triangular matrix solves which are computed using a standard backward-forward sequential algorithm. Unfortunately, this implementation prevents it from being accelerated with OpenACC. There exists more advanced triangular solvers, and for GPUs, the NVIDIA cuSparse library contains two such methods [4].
Since we were not certain our algorithms would achieve the desired performance on GPUs, we decided it was best to first test them using a much smaller code that uses the identical PCG solver from MAS called POT3D. After implementing OpenACC and linking the code to cuSparse for the PC2 algorithm, we found that our matrices were not suitable for efficient triangular matrix solves using cuSparse, resulting in PC1 and PC2 having nearly the same performance on GPUs. However, the performance was still quite good compared to runs on the CPU (even using PC2!). Therefore for MAS, we only need to implement PC1, which has the huge benefit of keeping the code portable! (For more details of our POT3D implementation, see [5-6]). After the success of this proof-of-concept, the initial MAS implementation got the green light.
Diving In! OpenACC Implementation Details
Now let’s delve into some of the more important and/or less-common details of implementing OpenACC that we used in porting MAS.
The OpenACC Do Loop
Below is an example of OpenACC applied to a triple-nested stencil operation do loop in MAS:
!$acc kernels default(present) present(ps) async(1) !$acc loop independent do k=2,npm1 !$acc loop independent do j=2,ntm1 !$acc loop independent do i=2,nrm-1 ii=ntm2*(nrm-2)*(k-2)+(nrm-2)*(j-2)+(i-1) q(ii)=a_r( i,j,k,1)*ps%r(i ,j ,k-1) & +a_r( i,j,k,2)*ps%r(i ,j-1,k ) +... enddo enddo enddo !$acc end kernels c ... two similar loops ... !$acc wait
The
present(ps) clause in this loop is needed due to a current bug in the PGI compiler (as of v18.4). The default(present) doesn’t detect the derived type properly. Using the explicit present avoids the problem.The kernels directive tells the compiler to parallelize the loop; the default(present) clause tells the compiler that we have already put all the data arrays on the GPU. The loop directive informs the compiler that the loop should be parallelized while the independent clause tells the compiler that we are certain each loop iteration is independent from each other and can be computed in a SIMD fashion (needed, due to the ii index computation). The async(1) clause tells the compiler to execute the loop on its own independent CUDA stream (an !$acc wait clause is later used to synchronize streams). The compiler chooses a parallelization mapping topology for each loop, deciding how the work is to be spread across the device. For the above code, the PGI compiler (v18.4) outputs:
23645, Generating implicit present(a_r(2:nrm-1,2:ntm1,2:npm1,1:15))
Generating present(ps)
Generating implicit present(q(:))
23647, Loop is parallelizable
23649, Loop is parallelizable
23651, Loop is parallelizable
Accelerator kernel generated
Generating Tesla code
23647, !$acc loop gang ! blockidx%y
23649, !$acc loop gang, vector(4) ! blockidx%z threadidx%y
23651, !$acc loop gang, vector(32) ! blockidx%x threadidx%x
An alternative to using the kernels directive, is to use the parallel directive which implicitly implies the independent clause. Using parallel can be useful if many separate loops in a row are independent as it generates a single GPU kernel, while the !$acc kernels directive will typically generate a separate kernel for each loop causing more kernel launch overhead. We chose to use kernels here because we will find that the compiler generates more efficient code for this loop compared to using parallel.
What if there Isn’t a Do? Dealing with FORTRAN Array-Syntax
FORTRAN supports “array syntax” where arrays are operated element by element without needing an explicitly written loop, such as f(:)=a(:)*x(:)+b(:)*y(:). You cannot apply OpenACC directives as above to these “loops” since there are no “do” loops to place the “loop” clauses. To avoid having to write out the loop explicitly (which could involve a lot of code changes), you can simply place !$acc kernels around the array-syntax code and the compiler will attempt to generate parallel kernels:
!$acc kernels default(present) f(:)=a(:)*x(:)+b(:)*y(:) !$acc end kernels
However, sometimes the compiler may have difficulty since there is no equivalent to the loop independent clause. In such cases, you are left with no other choice than to write out the loops. You may want to do this anyway in cases where there are many array syntax operations in a row since the kernels directive will make separate GPU kernels for each one, while combining them into one set of loops can generate a single kernel, avoiding launch overheads.
We used the kernels directive whenever possible to avoid code rewriting for MAS, but did need to convert a few array syntax code segments into explicit loops.
Data Management: Unified/Managed Memory vs. Unstructured Data Regions
Avoiding data transfers between the CPU and GPU is a frequently-cited mantra of GPU programming. These generate high
Make sure that the call
!acc exit data delete(a) comes before deallocating the CPU version of the array!latencies due to slow transfer rates. Unstructured data regions represent one way to transfer data to the GPU and have it available for as long as the user needs. For example you might use, !$acc enter data copyin(a) which copies data element a to the device, or !$acc enter data create(a) which allocates the space for a on the device, without initialization. These are followed up by a corresponding !$acc exit data delete(a) clauses when the data element is no longer needed. This method of data transfer can be done anywhere in the code including global arrays within modules, avoiding copying the data back and forth multiple times.
We copy all the main field arrays in MAS after computing their initial conditions on the CPU. These fields stay on the device for the entire simulation, only updating them on the host (using the !$acc update self() directive) when needed for file output. We allocate/deallocate temporary arrays used in subroutines using the create and delete data clauses.
An attractive alternative to manually managing the GPU-CPU data transfers is to use CUDA Unified Memory through PGI’s “managed memory” option. This option causes all your array allocations to be performed as CUDA unified memory allocations, allowing automatic paging when using the arrays on the GPU. This not only eliminates the need to worry about data transfers but for modern GPUs, also enables you to use more data than the GPU’s memory capacity (albeit with a performance hit).
Managed memory is no panacea, however. Currently, it only supports allocated arrays, so any static arrays must still be manually managed. Also, this feature may fill the memory of the GPU and page swap more than needed, degrading performance. Generally, you’ll see better performance when managing the memory manually than relying on unified memory. Since managed memory is currently a PGI-only feature (i.e. not part of the OpenACC API), there are also portability concerns. Finally, while it might be a nice idea to use managed memory at first and later migrate to manual memory management for performance, such a transition can be a surprisingly large, all-or-nothing step.
For MAS, we started out using managed memory and was able to get it to work for some regions of the code. Eventually, we needed to switch to manually managing the data due to some compiler issues involving derived types. This was not a major problem as we had planned to do this anyway for performance reasons. However, this step ended up taking quite some time to get right.
Derived Types: “True” vs. “Manual” Deep-Copy
Derived types pose a difficulty in transferring data to and from the GPU since the type object needs to be transferred to the GPU in addition to any arrays it may contain. A type may also contain other types, which contain types, etc. down multiple levels with arrays at each stage. Copying the entire type structure with all of its contents included is referred to as “deep-copy”. The OpenACC API does not currently support such a “true” deep-copy, but does support “manual” deep-copy. For example, let’s say you have a type defined as:
type :: t1 real, dimension(:), allocatable :: x type(t2) :: y end type
where the type t2 is defined as:
type :: t2 real, dimension(:), allocatable :: z end type
When transferring a derived type with its arrays in a single data directive, be sure to list the types before their contents in the list. When exiting the data, the order should be reversed!
To copy an (already allocated) instance of this type (e.g., type(t1) :: a) to the GPU, you would use !$acc enter data copy(a,a%x,a%y,a%y%z). Placing all subtypes and their contents in one data directive avoids having to use the attach clause (see the OpenACC 2.6 spec for more information).
PGI has implemented a custom automatic “true” deep-copy compiler option which allows transferring entire types at once (e.g. for the example above, !$acc enter data copy(a)). This can be a lifesaver if your code has enormous and/or very deep type structures, saving you from writing long data directives.
While we first implemented the data type transfers in MAS using the PGI deep-copy feature, due to some compiler bugs at the time (it was a brand new feature), and our desire to adhere to the official OpenACC spec (for portability), we currently only use manual deep-copy. Luckily the types used in MAS are typically only one or two levels deep and do not contain many entries, so this does not clutter up the code too much.
Wait… That Routine is Called by the CPU too…
Certain routines in your code that are called in heavy computational regions may also be used in regions of the code you do not want to (nor should) accelerate with OpenACC. This is especially true in very large codes. For example, in MAS, several routines used during the setup of the initial condition are also used in the main solvers. The setup phase takes very little time on the CPU and contains a vast number of additional routines that would take quite some time to apply OpenACC.
One potential fix for this situation is to use the conditional clauses in OpenACC within those routines. These clauses allow an OpenACC region to only use the GPU if a condition is met. This condition could be as simple as a logical variable that you can switch on and off in the regions of code you need. Another type of conditional clause in OpenACC is if_present that will only use the GPU code if the arrays used in the region are present on the device. Currently, only a subset of directives can use the general conditional clauses, while a different subset can only use if_present. Unfortunately, there can be cases where the array in question does exist on the device (for example, it has been allocated) but is not being used yet. In that situation, the if_present would not help (MAS had examples of this).
We wanted to avoid adding new parameters to the MAS code or having to add conditional clauses to every OpenACC loop (messy!). So for now, we simply made duplicates of those few routines that are required by the setup; one version with OpenACC and the other without. (Both work on the CPU when the code is compiled without GPU acceleration). After the entire code is ported, the number of these duplicated routines should eventually be at a bare minimum. Future OpenACC API development may also lead to new solutions to this small problem.
Array Reductions
Reduction operators are ubiquitous in many codes; from computing dot products to calculating averages. For a scalar variable, OpenACC includes a reduction clause as shown here:
real(8) :: sum=0 !$acc kernels loop reduction(+:sum) present(a) do j=1,m sum=sum+a(j) enddo
However, often you come across the need for a collective operation along an array, for example:
allocate(sum(n)) sum(:)=0 do j=1,m sum(:)=sum(:)+a(:,j) enddo
Unfortunately, OpenACC does not currently have a way to directly express this kind of reduction to the compiler. Table 1 shows two examples on how to implement the above reduction:
| Example (1) | Example (2) |
!$acc kernels !$acc loop do j=1,m !$acc loop do i=1,n !$acc atomic update sum(i)=sum(i)+a(i,j) enddo enddo !$acc end kernels |
!$acc kernels loop do i=1,n sum(i)=SUM(a(i,1:m)) enddo |
The result that example (1) is faster than (2) is highly specific to the problem and the hardware. There may exist more ways to do this that may perform better. Go find them and let us know!
Example code (1) keeps the loops in “stride-1” order. On the inner loop, you might think you can use something like !$acc loop reduction(sum(i)), but this syntax is not recognized by OpenACC. This is because since the “j” loop is parallelized, two threads with different “j’s” may try updating sum with the same “i”. In order to prevent this, the atomic directive is required. Atomic operations can be quite slow on older GPU models, but we have found good performance using them with both Pascal and Volta architectures. Example code (2) inverts the loops and only parallelizes the outer loop. Although this avoids using atomics and is a more compact form of the code, it suffers from having out-of-order memory accesses and only parallelizing along one (possible short) dimension. So which one to use? To find out, we profiled the code with pgprof and found that example (1) was faster than (2) both on the CPU and GPU. Although we now use example (1), due to our hesitation using atomics at the time, the results in this blog used example (2).
It’s Not Good for GPUs to Compute Alone: Multiple Devices
Getting the best performance from your code will likely mean using multiple GPUs, both within a compute node/server and between nodes on a cluster. Another reason to use multiple GPUs is that GPU memory is small compared to CPUs; your problem might be too large to fit on a single GPU.
To use multiple GPUs, let’s assume that the code in question is already parallelized across CPUs using MPI, as it is in MAS (if your code uses OpenMP, see [7]). We then need a way to tell the OpenACC API which GPU we want a specific MPI rank to compute with. This can be done by using the !$acc set device_num() directive. It tells the compiler that any OpenACC code after hitting this directive should be performed on the device specified. So if you want each MPI rank to control 1 GPU (a typical arrangement), you could do something like:
call MPI_Comm_rank (MPI_COMM_WORLD,iprocw,ierr) ngpus_per_node = 4 igpu = MODULO(iprocw, ngpus_per_node) !$acc set device_num(igpu)
Easy, right? Problem! The above code assumes linear affinity of the ranks across all cores and nodes on the cluster. While this is sometimes the case, it is by no means certain. You could make sure to set up a machine file and/or advanced mpiexec command arguments for your specific system, but there is a more portable way. MPI-3 has the ability to create a node-level communicator with its own local ranks. These “shared” communicators are quite easy to set up and can be used for our purposes as shown here:
If you want to oversubscribe the GPUs, make sure you have Multi-Process Services (MPS) active in the driver. See NVIDIA’s MPS Overview for more details.
call MPI_Comm_split_type (MPI_COMM_WORLD,MPI_COMM_TYPE_SHARED,0, & MPI_INFO_NULL,comm_shared,ierr) call MPI_Comm_size (comm_shared,nprocsh,ierr) call MPI_Comm_rank (comm_shared,iprocsh,ierr) igpu=MODULO(iprocsh,nprocsh) !$acc set device_num(igpu)
While the above code assumes that you have set the number of MPI ranks per node equal to the number of GPUs per node, this is not required. You could easily modify the code to allow oversubscription of the GPUs.
Performance Enhancers
At this point, you (hopefully) have a working OpenACC version of your code — at least in the computational heavy parts. Now let’s optimize performance!
Does Your MPI Library Recognize GPUs?
Previously, we showed that using the unstructured data directives and/or managed memory allows us to keep our data on the GPU as much as possible. However, when using multiple GPUs with MPI, data gets transferred to the CPU, used in the MPI calls, and then the received data is transfered back. Fortunately, these transfers can be avoided using what is known as “CUDA-aware” MPI. This feature is implemented in nearly all major MPI libraries. In short, the CUDA-aware MPI allows you to directly use your device arrays in MPI calls, theoretically eliminating the need for GPU-CPU transfers. Ideally, your CUDA-aware MPI library will bypass the CPU completely through the use of direct RDMA transfers from GPU to GPU on available hardware. However, it is entirely up to the MPI library on how it implements this and, in some cases, may even default to using GPU-CPU transfers for best MPI-based performance. Therefore, it is very important to choose and set up your MPI library, hardware, and system drivers carefully for the best MPI-based multi-GPU performance.
In the current version of PGI (v18.4), there’s a bug where if you pass a derived type into a routine and try to use its members in CUDA-aware MPI calls, the code fails. To work around this, modify the routine’s signature to input the type’s members directly (as simple arrays).
In order to tell the compiler to use the device arrays in an MPI call, we use the !$acc host_data use_device directive. To illustrate this, below we show an example of a stencil boundary update from MAS:
c ****** Load buffers. !$acc enter data create(sbuf11,sbuf12,rbuf11,rbuf12) !$acc kernels default(present) sbuf11(:,:)=x(n1-1,:,:) sbuf12(:,:)=x( 2,:,:) !$acc end kernels c ****** Start transfers. !$acc host_data use_device(sbuf11,sbuf12,rbuf11,rbuf12) call MPI_Irecv (rbuf11,lbuf1,ntype_real,iproc_rm,tag,comm_all,req(1),ierr) call MPI_Irecv (rbuf12,lbuf1,ntype_real,iproc_rp,tag,comm_all,req(2),ierr) call MPI_Isend (sbuf11,lbuf1,ntype_real,iproc_rp,tag,comm_all,req(3),ierr) call MPI_Isend (sbuf12,lbuf1,ntype_real,iproc_rm,tag,comm_all,req(4),ierr) c ****** Wait for all transfers to complete. call MPI_Waitall (4,req,MPI_STATUSES_IGNORE,ierr) !$acc end host_data c ****** Unload buffers. !$acc kernels default(present) if (iproc_rm.ne.MPI_PROC_NULL) then x(1,:,:)=rbuf11(:,:) end if if (iproc_rp.ne.MPI_PROC_NULL) then x(n1,:,:)=rbuf12(:,:) end if !$acc end kernels !$acc exit data delete(sbuf11,sbuf12,rbuf11,rbuf12)
The Dark Side of Data Residency, or, “Do I Really Need to Accelerate All these Routines???”
In keeping with the data residency theme, although the use of data directives and CUDA-Aware MPI can keep the data on the GPU as much as possible (barring any I/O, etc.), another key requirement is that every single part of the computation using the data must be accelerated. While this may sound obvious, it can cause quite a headache because it may be the case — as it was for us in MAS — that your code contains many small or hard-to-accelerate routines and loops. Accelerating all these routines can have a substantial impact on development time. However, it is still a good idea to go ahead and accelerate them (even if they run inefficiently on the GPU) because you will reap an overall performance benefit by avoiding the data transfers.
Loop Optimization: “You must Unlearn what you have Learned…”
If you’ve always been taught “stride-1 is best!”, sometimes that may not be the case! Take a look at the two example loops in figure 2. While the two loops appear very similar, they differ in the memory layout of the matrix coefficients stored in a_r. In figure 2 (left), the array is transversed in a perfect stride-1 fashion, ensuring that a large piece of data resides in cache, speeding up access to said data (i.e. cache-friendly). However, this stride-1 layout is not aligned with the i-j-k loop, hindering SIMD vectorized instructions.

In figure 2 (right), each of the 15 coefficients in a_r are far apart in memory, behaving like 15 unique memory streams, which can be quite slow on the CPU depending on the size of the cache. However, each of these memory streams is now stride-1 accessible for the i-j-k loops, enabling large SIMD instructions to be executed (i.e. vector-friendly).
We seemed to have a trade-off with GPU vs CPU performance which was problematic considering our goal of having only one code base. In order to decide which loop to use, we performed timings with both methods using a test run similar to that described below, and recorded the wall clock time of the runs. (These modified loops account for ~60% of the wall clock time). We also took this opportunity to test the code as it was when we started this venture versus the code with the few CPU code modifications we needed for the OpenACC implementation so far.
You can see the results in figure 3. The first thing you notice is that the CPU code does indeed slow down when using the “vector-friendly” loops, but happily, this slow down is quite small. In fact, the performance decrease is less than the speedup gained in the OpenACC development modifications made to the CPU code. Therefore, we can safely use the “vector-friendly” loops with little-to-no detriment to the CPU runs.
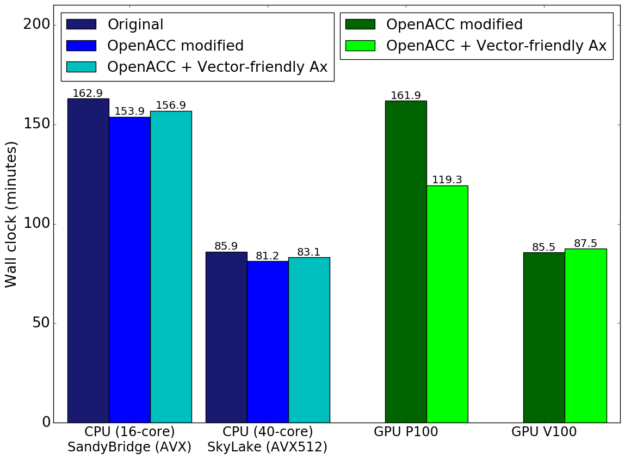
It is curious to note that using the wider AVX-512 vector instructions for the vector-friendly loops on the SkyLake processors did not exhibit improved relative performance compared to the smaller AVX instructions on the Sandy Bridge processors. This may be due to the requirement to use additional compiler options (more than just -xAVX-512) to enable the full-width vectorization capabilities of AVX512-capable CPUs which, if used, lowers CPU clock frequency.
On the GPU side of things, the P100 using the “vector-friendly” loops has a very significant performance boost compared to the “cache-friendly” alternative (keep in mind these are full wall-clock results, not just the isolated routine). Surprisingly, (and unfortunately) we do not see such performance boost on the V100, and in fact see a slight performance decrease. Although we do not know why this is case, due to the P100 results and the very little slow down on other architectures, we opted to use the “vector-friendly” loops (a small change to the CPU code).
Parallel, Kernels, Gangs, Workers, Vectors … oh My!
An OpenACC compiler has the tough job of converting serial code into parallel code to run on a specified device. Each compiler vendor will implement some kind of default parallelism when encountering a kernels or parallel region. In order to fine-tune performance, OpenACC contains directive clauses that you can use to give hints/direction to the compiler to parallelize your loops as you desire. These include the gang, worker, and vector topology clauses, as well as more advanced clauses such as cache and tile.
Navigating these options and choosing their variable parameters (such as vector length) can be daunting due to the plethora of possible combinations. Knowledge about the device you are targeting can guide you to a subset of reasonable options but even this subset can be very large. So what should you do? For MAS, we took the same loop code used above (accounting for 60% of the wall clock time) and tested it with numerous topology choices including the default for parallel and kernels. Figure 4 shows the timing results of the routine (by itself) for each choice we tried.

We see that there is a factor of over 3X in performance between the fastest and slowest options we tried. This implies that choosing the topology is critically important. Luckily for us, the fastest option happened to be the default (no topology clauses) when using kernels. This result will obviously be compiler dependent, but at least for MAS with PGI, we did not need to use any of the topology clauses to get good performance. For your code and compiler, running a series of tests like those above is currently the only real way of finding the best parameters.
The Cutting Edge can be Quite Sharp
So your going along, happily implementing OpenACC, taking into account all the tips, strategies, and optimizations you’ve been reading about here and elsewhere and go to test your code. Everything should work great right? Don’t be so sure…
I Thought the Compiler Supported that!
Sometimes not all details of a new features are documented or eagerness to try them out overrides caution, leading to time-consuming implementation mistakes. Some examples we encountered were the proper order of derived types and their members in a data clause, needing to use use_device(a%r) instead of use_device(a) for derived type arrays in host_data directives, and basically all the “bug watch” items mentioned above. Also, sometimes certain combinations of new features are simply not implemented yet (for example, in the current community edition of PGI (v18.4), you cannot use the cache clause on arrays within derived types).
Like all large complex software packages, compilers can have bugs, which can create major development issues. It is therefore vital to use a well-supported, actively-developed compiler. Even with that, you may need to wait weeks or even months for a bug to be fixed before your code can work. Sometimes, temporary workarounds can be used, but other times, you are simply stuck.
In our OpenACC development of POT3D and MAS, we encountered our share of compiler bugs in PGI, all of which currently have workarounds or have been fixed. Some examples included:
- Crashing when using multi-level derived types (fixed in v17.10)
- Requiring an explicit
present(a)alongsidedefault(present)when using derived types, (not yet fixed) - Crashing when using derived type members in
host_data use_devicedirective around CUDA-aware MPI, (started in v17.10 and not yet fixed)
Although dealing with these bugs can be frustrating and time-consuming, the compiler vendors typically respond promptly and are very helpful in finding temporary work-arounds, as well as pushing bug fixes rapidly.
I Thought the HPC System Supported that!
Bugs squashed. Code working on your local server. Now you’re ready to run it on a GPU-enabled cluster. You log in, transfer your code and test run, compile, set up the queue, and are all set to go. The run starts, and… seg fault!
Depending on the priority of GPU computing on the specific cluster you are using, the HPC system may be “behind-the-times” in terms of software. For example, the MPI library may be too old to support CUDA-Aware MPI, or the compiler too old to support the version of OpenACC you need. Even if the software stacks are up to date, hardware setup and interlibrary bugs can crop up, especially if you are running in a manner that has not been tried too often (or ever). In some cases, licensing issues may prevent a center from installing a needed compiler or driver.
In testing our POT3D and MAS ports on clusters, we encountered these issues on more than one machine. In one instance, the MPI library had a bug that prevented CUDA-aware MPI from working at all. In another, the only PGI compiler available was a version before a needed bug fix was implemented, and its license had expired! On another cluster, a setup problem was causing all multi-GPU runs to simply crash. Many of these problems were on machines whose GPU features were secondary and no one had tried multi-GPU OpenACC code previously. Happily, the staffs helped us find ways to get things working. On HPC systems designed specifically for GPU computation, these kinds of problems should be much more rare. Containers have great promise in alleviating these difficulties as well [8].
All these issues of implementation mistakes, compiler bugs, and environment/system incompatibility should be factored into development time estimates, as they can be (and were) quite time-consuming.
So after all that … How Involved was this?
Just like commercial flying is the fastest and safest way to travel, yet there is a little baggie in every seat pocket, so to, OpenACC is one of the fastest, efficient, and portability-safe ways to accelerate your code, but don’t expect it to be a walk in the park. In our case, the actual OpenACC coding of the initial porting of MAS (to our targeted subset feature mode) was actually quite straightforward and required very little CPU code changes (many of which increased the CPU performance!). One time-consuming task that stood out was having to accelerate many small routines to keep the data on the GPUs. We summarize the required code modifications in terms of OpenACC directives and CPU code changes in Table 2:
| Total lines in original code | 51,591 |
| Total lines in accelerated code | 54,191 |
| Total !acc/!acc& lines added | 671 (1.3%) |
| Total modified lines | 844 (1.6%) |
| Total number of additional lines | 2,600 (5.0%) |
| Total number of different lines | 4,314 (8.2%) |
We see that we only needed to add OpenACC directive amounting to roughly 1% of the code’s total lines of code, and modified under 2% of the CPU code (some of which were optional optimizations). We ended up adding a total of 5% lines of code, many of which can be removed once some compiler bugs are fixed and new API features are added to OpenACC. However, remember that this implementation only covers the Zero-Beta feature set in MAS. Once our complete implementation is done, the amount of modification will be higher.
Although the OpenACC coding was a fairly smooth ride, the most turbulent and time-consuming part of our development turned out to be working around compiler and library bugs, and dealing with issues on the HPC systems as discussed above. However, we expect that as the compilers, HPC systems, MPI libraries, and the OpenACC API continue to grow and improve, these difficulties will drastically decrease.
OK OK … but Did it Work? Let’s See Some Numbers!
What is a “fair” timing?
There is no truly “fair” way to compare GPU and CPU performance of a given code since the optimal implementation of the algorithms are often unique for each hardware (either explicitly in the code, or implicitly through the compiler). Also, some algorithms may perform better on one hardware than the other, while others will be the reverse (e.g. our PC2 preconditioner is more suited for a CPU, while the PC1 is best on a GPU).
Luckily, domain scientists (like us) are not in the business of hardware benchmarking, and really only care about the effective “time-to-solution” for a problem. In this light, a “fair” comparison is testing our code on each hardware using the best algorithm, compiler, and environment we currently have available. There is always room for improvement (such as research into more vectorizable algorithms), but here we want to see what kind of GPU performance we can get using our current code algorithms accelerated using OpenACC.
It is unfortunately common to see performance results reported only for the regions of code that were accelerated, but not the full wall time. Since we care about the time-to-solution, such results can be misleading (and artificially avoid Amdahl’s law). Here, we record the absolute wall clock time of our runs including all CPU-code setup, I/O, CPU-GPU transfers, etc. While we do not include the wait queue time on the HPC systems, the time waiting for your job to run should not be ignored, as it can become quite long for large runs and/or when the HPC cluster is busy.
Another common problem in performance testing is the use of “toy” problems. These may yield great results, but are not relevant to the actual use of the code. In some cases, using such simplified problems may be unavoidable (e.g. the code takes days to run a real problem) but in general this should be avoided. Here, we test our code’s performance using a `real-world’ production simulation, including a large amount of in-situ diagnostics and file output.
The Test Problem
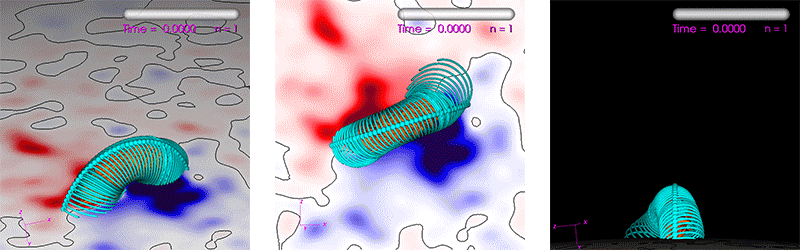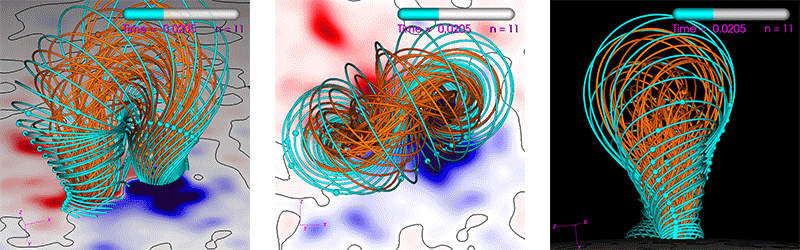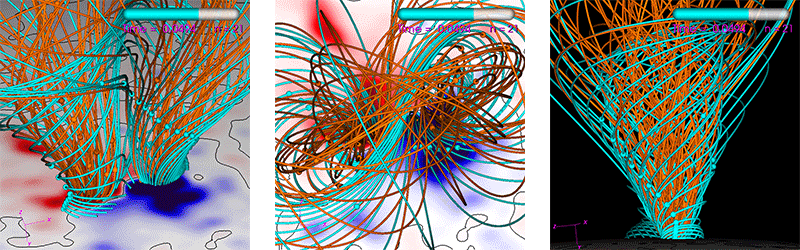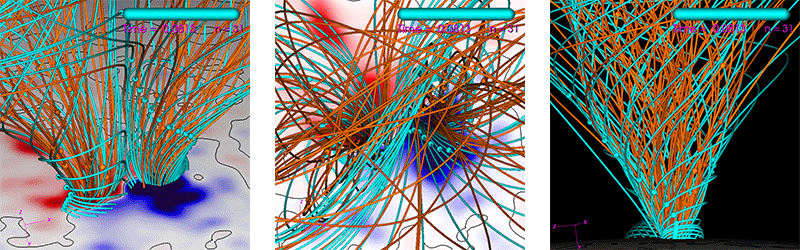
The run we use is a Zero-Beta MHD simulation of the eruption of a CME (see reference [9] for similar simulations). It uses a non-uniform spherical grid with 33 million points. The average number of solver iterations per time step over the run is ~500 for PC1 and ~100->200 for PC2 (the PC2 degrades in iteration reduction as the number of MPI ranks increase). All computations are performed using double-precision (FP64). The run’s parameters are generated by our interactive tool used to study CME eruptions. This tool has a heuristic estimate (balancing performance and resource use) of how many CPU cores one should use in order to achieve an “acceptable” time-to-solution. We use this “acceptable” time-to-solution as a baseline to judge performance. For the run used here, it is estimated to be 90 minutes using 16 dual-socket Haswell nodes equaling 384 CPU cores. Figure 5 shows visualizations of the run.
Details of the Environment
Table 3 shows some details of the hardware and software environments used for the performance runs. The CPU runs were performed using NASA NAS’s Pleiades and Electra supercomputers, while the GPU runs were performed on NVIDIA’s PSG test cluster. All codes were compiled with “-O3” and the highest instruction set/compute-capability compatible with the respective hardware.
| NASA NAS
Pleiades & Electra |
NVIDIA PSG | |
| Compiler | Intel 2018 .0.128 | PGI 17.9 |
| MPI Library | SGI MPT 2.15r20 | OpenMPI 1.10.7 |
| Intel Family | Haswell (Pleiades) / Skylake (Electra | N/A |
| Instruction Set | AVX2 (Haswell), AVX512 (Skylake) | N/A |
| Driver Version | N/A | 387.26 |
| CUDA Library | N/A | 9.0.176 |
| Processor | E5-2680v3 (Haswell) / Gold 6148 (Skylake) | P100 PCIe / V100 PCIe |
| Clock Frequency | 2.5GHz (Haswell) / 2.4Ghz (Skylake) | 1.33GHz (P100) / 1.38GHz (V100) |
| Core Count | 2×12 (Haswell) / 2×20 (Skylake) | 1792 (P100) / 2560 (V100) (CUDA FP64 Cores) |
| GPUs per Node | N/A | 4 |
| Memory Bandwidth | 68GB/s (Haswell) / 128GB/s (Skylake | 732GB/s (P100) / 900GB/s (V100) |
Performance Results
The timing results using multiple CPU nodes and GPU models are shown in figure 6.
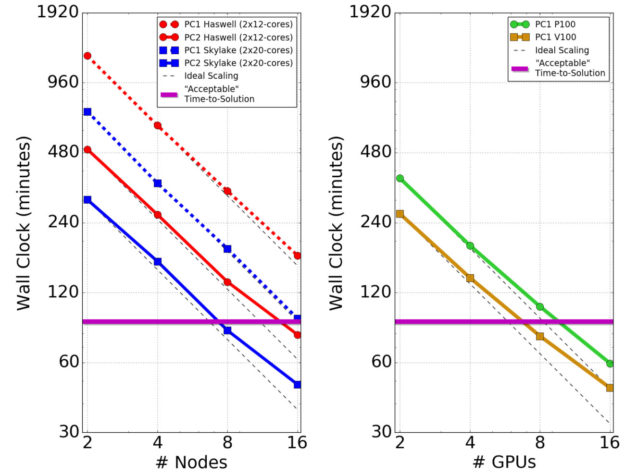
The primary take-away from these results is that we achieved the “acceptable” time-to-solution using a number of GPUs that can fit into a single in-house server. We required ~16 24-core Haswell nodes or ~8 40-core Skylake nodes to achieve the same run time using CPUs. Therefore, we can move from needing a HPC cluster to running in-house on problems of this kind. We also see that the PC1 algorithm scales better on the CPUs than PC2, but PC2 is still much faster overall.
On the GPUs, we see good scaling up to 4 GPUs, but the scaling gets worse past that. This is likely due to the fact that the system we tested on has 4 GPUs per node and lacks any GPUDirect/RDMA capability. We expect the scaling to be better when using up to 16 GPUs on a single multi-GPU server (up to 5 in a desktop workstation), especially those equipped with NVLink such as the DGX-Station, DGX-1, and DGX-2. Another possible reason for the falloff in scaling may be that the current problem is simply too small to efficiently employ more than a few GPUs.
To illustrate the GPU performance advantage in an in-house setting, figure 7 shows timing results (in hours) using a single dual-socket CPU server versus using up to 8 GPUs. Department servers tend to be dual-socket configurations, or perhaps quad-socket at best.
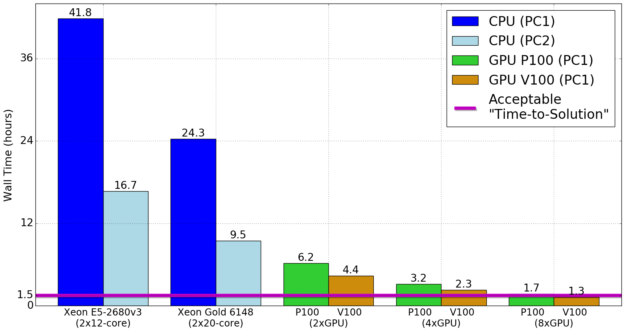
Although we have focused on using GPU acceleration to run small-to-medium simulations in-house, we can easily expect to be able to take full advantage of large GPU-based HPC clusters such as the recently deployed Summit supercomputer at ORNL which uses 6 NVIDIA Volta GPUs per node interconnected with NVLink and RDMA across nodes. Using such systems would allow us to run large simulations using less allocation resources, as well as achieving faster “time-to-solutions” by requiring running on fewer total nodes, avoiding long wait queues.
What’s Next?
Our next steps in the OpenACC implementation of MAS, are primarily to implement the remaining physics modules and feature sets, allowing us to use GPU-acceleration for state-of-the-art CME simulations. We will also be looking into using new vectorizable preconditioners for the PCG solves, and/or alternative algorithms for better GPU performance. For example, preliminary testing with the RKL2 Super Time-stepping method [10] has shown very promising results.
I’m Convinced! Where Can I Get Started?
If you are interested in using OpenACC for your code, you can find many great tutorials and information at the OpenACC resources site, which include presentations, books, tutorials, recorded courses, sample codes, and upcoming workshops and hackathons. GTC on-demand is a great place to get started with many talks and hands-on tutorials. Hackathons are a fantastic resource where you and your team can work for a week with OpenACC experts on your code. Ready to get started? Head on over to PGI, download the free community edition compiler, and start testing! If you’re also interested in more details on our MAS implementation, check out our talk from GTC 2018.
Acknowledgements
This work was supported by the National Science Foundation, NASA’s Living with a Star and Heliophysics Supporting Research programs, and the Air Force Office of Scientific Research Computational resources were provided by NASA’s Advanced Supercomputing Division and the NVIDIA Corporation.
References
[1] http://www.predsci.com/eclipse2017
[3] Predicting the Corona for the 21 August 2017 Total Solar Eclipse Z. Mikic, C. Downs, J. A. Linker, R. M. Caplan, D. H. Mackay, L. A. Upton, P. Riley, R. Lionello,T. Torok, V. S. Titov, J. Wijaya, M. Druckmuller, J. M. Pasachoff, and W. Carlos. Submitted to Nature Astronomy (2018)
[4] https://docs.nvidia.com/cuda/cusparse
[5] Potential Field Solutions of the Solar Corona: Converting a PCG Solver from MPI to MPI+OpenACC R. Caplan, J. Linker, and M. Zoran. Presented at the 2017 NVIDIA GPU Technology Conference http://on-demand.gputechconf.com/gtc/2017/video/s7535-ronald-caplan-potential-field-solutions-of-the-solar-corona-converting-a-pcg-solver-from-mpi-to-mpi+openacc.mp4
[6] From MPI to MPI+OpenACC: Conversion of a legacy FORTRAN PCG solver for the spherical Laplace equation R. Caplan, J. Linker, and M. Zoran. arXiv:1709.01126 [cs.MS] (2017)
[7] https://www.slideshare.net/jefflarkin/early-results-of-openmp-45-portability-on-nvidia-gpus-cpus
[8] https://developer.nvidia.com/blog/gpu-containers-runtime/
[9] Mikic, Z., Torok, T., Titov, V., et al. 2013, Solar Wind 13, 1539, 42
[10] Meyer C D, Balsara D S and Aslam T D 2014 Journal of Computational Physics 257 594–626