This series of posts aims to highlight some of the main differences between conventional programming and parallel programming on the algorithmic level, using broad-phase collision detection as an example. The first part will give some background, discuss two commonly used approaches, and introduce the concept of divergence. The second part will switch gears to hierarchical tree traversal in order to show how a good single-core algorithm can turn out to be a poor choice in a parallel setting, and vice versa. The third and final part will discuss parallel tree construction, introduce the concept of occupancy, and present a recently published algorithm that has specifically been designed with massive parallelism in mind.
Why Go Parallel?
The computing world is changing. In the past, Moore’s law meant that the performance of integrated circuits would roughly double every two years, and that you could expect any program to automatically run faster on newer processors. However, ever since processor architectures hit the Power Wall around 2002, opportunities for improving the raw performance of individual processor cores have become very limited. Today, Moore’s law no longer means you get faster cores—it means you get more of them. As a result, programs will not get any faster unless they can effectively utilize the ever-increasing number of cores.
Out of the current consumer-level processors, GPUs represent one extreme of this development. NVIDIA GeForce GTX 480, for example, can execute 23,040 threads in parallel, and in practice requires at least 15,000 threads to reach full performance. The benefit of this design point is that individual threads are very lightweight, but together they can achieve extremely high instruction throughput.
One might argue that GPUs are somewhat esoteric processors that are only interesting to scientists and performance enthusiasts working on specialized applications. While this may be true to some extent, the general direction towards more and more parallelism seems inevitable. Learning to write efficient GPU programs not only helps you get a substantial performance boost, but it also highlights some of the fundamental algorithmic considerations that I believe will eventually become relevant for all types of computing.
Many people think that parallel programming is hard, and they are partly right. Even though parallel programming languages, libraries, and tools have taken huge leaps forward in quality and productivity in recent years, they still lag behind their single-core counterparts. This is not surprising; those counterparts have evolved for decades while mainstream massively parallel general-purpose computing has been around only a few short years.
More importantly, parallel programming feels hard because the rules are different. We programmers have learned about algorithms, data structures, and complexity analysis, and we have developed intuition for what kinds of algorithms to consider in order to solve a particular problem. When programming for a massively parallel processor, some of this knowledge and intuition is not only inaccurate, but it may even be completely wrong. It’s all about learning to “think parallel”.
Sort and Sweep
Collision detection is an important ingredient in almost any physics simulation, including special effects in games and movies, as well as scientific research. The problem is usually divided into two phases, the broad phase and the narrow phase. The broad phase is responsible for quickly finding pairs of 3D objects than can potentially collide with each other, whereas the narrow phase looks more closely at each potentially colliding pair found in the broad phase to see whether a collision actually occurs. We will concentrate on the broad phase, for which there are a number of well-known algorithms. The most straightforward one is sort and sweep.
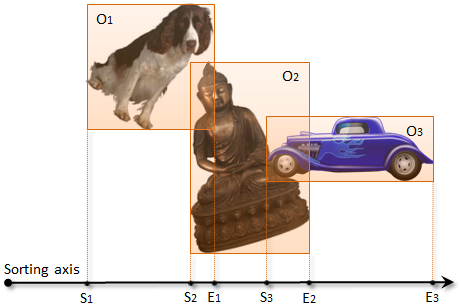
The sort and sweep algorithm works by assigning an axis-aligned bounding box (AABB) for each 3D object, and projecting the bounding boxes to a chosen one-dimensional axis. After projection, each object will correspond to a 1D range on the axis, so that two objects can collide only if their ranges overlap each other. 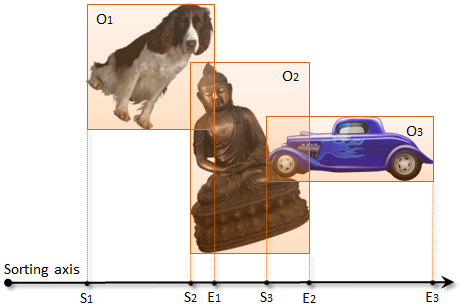
In order to find the overlapping ranges, the algorithm collects the start points (S1, S2, S3) and end points (E1, E2, E3) of the ranges into an array, and sorts them along the axis. For each object, it then sweeps the list from the object’s start and end points (e.g. S2 and E2) and identifies all objects whose start point lies between them (e.g. S3). For each pair of objects found this way, the algorithm further checks their 3D bounding boxes for overlap, and reports the overlapping pairs as potential collisions.
Sort and sweep is very easy to implement on a parallel processor in three processing steps, synchronizing the execution after each step. In the first step, we launch one thread per object to calculate its bounding box, project it to the chosen axis, and write the start and end points of the projected range into fixed locations in the output array. In the second step, we sort the array into ascending order. Parallel sorting is an interesting topic in its own right, but the bottom line is that we can use parallel radix sort to yield a linear execution time with respect to the number of objects (given that there is enough work to fill the GPU). In the third step, we launch one thread per array element. If the element indicates an end point, the thread simply exits. If the element indicates a start point, the thread walks the array forward, performing overlap tests, until it encounters the corresponding end point.
The most obvious downside of this algorithm is that it may need to perform up to O(n2) overlap tests in the third step, regardless of how many bounding boxes actually overlap in 3D. Even if we choose the projection axis as intelligently as we can, the worst case is still prohibitively slow as we may need to test any given object against other objects that are arbitrarily far away. While this effect hurts both the serial and parallel implementations of the sort and sweep algorithm equally, there is another factor that we need to take into account when analyzing the parallel implementation: divergence.
Divergence
Divergence is a measure of whether nearby threads are doing the same thing or different things. There are two flavors: execution divergence means that the threads are executing different code or making different control flow decisions, while data divergence means that they are reading or writing disparate locations in memory. Both are bad for performance on parallel machines. Moreover, these are not just artifacts of current GPU architectures—performance of any sufficiently parallel processor will necessarily suffer from divergence to some degree.
On traditional CPUs we have learned to rely on the large data caches built right next to the execution pipeline. In most cases, this makes memory accesses practically free: the data we want to access is almost always already present in the cache. However, increasing the amount of parallelism by multiple orders of magnitude changes the picture completely. We cannot really add a lot more on-chip memory due to power and area constraints, so we will have to serve a much larger group of threads from a similar size cache. This is not a problem if the threads are doing more or less the same thing at the same time, since their combined working set is still likely to stay reasonably small. But if they are doing something completely different, the working set explodes, and the effective cache size from the perspective of one thread may shrink to just a handful of bytes.
The third step of the sort and sweep algorithm suffers mainly from execution divergence. In the implementation described above, the threads that happen to land on an end point will terminate immediately, and the remaining ones will walk the array for a variable number of steps. Threads responsible for large objects will generally perform more work than those responsible for smaller ones. If the scene contains a mixture of different object sizes, the execution times of nearby threads will vary wildly. In other words, the execution divergence will be high and the performance will suffer.
Uniform Grid
Another algorithm that lends itself to parallel implementation is uniform grid collision detection. In its basic form, the algorithm assumes that all objects are roughly equal in size. The idea is to construct a uniform 3D grid whose cells are at least the same size as the largest object.
In the first step, we assign each object to one cell of the grid according to the centroid of its bounding box. In the second step, we look at the 3x3x3 neighborhood in the grid (highlighted). For every object we find in the neighboring cells (green check mark), we check the corresponding bounding box for overlap.
If all objects are indeed roughly the same size, they are more or less evenly distributed, the grid is not too large to fit in memory, and objects near each other in 3D happen to get assigned to nearby threads, this simple algorithm is actually very efficient. Every thread executes roughly the same amount of work, so the execution divergence is low. Every thread also accesses roughly the same memory locations as the nearby ones, so the data divergence is also low. But it took many assumptions to get this far. While the assumptions may hold in certain special cases, like the simulation of fluid particles in a box, the algorithm suffers from the so-called teapot-in-a-stadium problem that is common in many real-world scenarios.
The teapot-in-a-stadium problem arises when you have a large scene with small details. There are objects of all different sizes, and a lot of empty space. If you place a uniform grid over the entire scene, the cells will be too large to handle the small objects efficiently, and most of the storage will get wasted on empty space. To handle such a case efficiently, we need a hierarchical approach. And that’s where things get interesting.
Discussion
We have so far seen two simple algorithms that illustrate the basics of parallel programming quite well. The common way to think about parallel algorithms is to divide them into multiple steps, so that each step is executed independently for a large number of items (objects, array elements, etc.). By virtue of synchronization, subsequent steps are free to access the results of the previous ones in any way they please.
We have also identified divergence as one of the most important things to keep in mind when comparing different ways to parallelize a given computation. Based on the examples presented so far, it would seem that minimizing divergence tilts the scales in favor of “dumb” or “brute force” algorithms—the uniform grid, which reaches low divergence, has to indeed rely on many simplifying assumptions in order to do that.
In my next post I will focus on hierarchical tree traversal as a means of performing collision detection, with an aim to shed more light on what it really means to optimize for low divergence.