As datasets get bigger, ensuring data security and integrity becomes increasingly important. Cryptographic techniques, such as inclusion proofs, data-integrity checks, consistency validation, and digital signatures, are essential for addressing these challenges and protecting critical workloads. That’s where cuPQC SDK v0.4 comes in. 

By offering powerful device functions capable of fusing multiple lightweight operations within a single kernel, cuPQC ensures rapid and efficient cryptographic computations. cuPQC, which includes the added benefit of Link Time Optimization (LTO) and device-side APIs, significantly enhances performance, making it an indispensable tool for high-speed cryptographic tasks.

cuPQC’s APIs allow users to fuse cryptographic circuits, processes, or larger composite functions into high-performance GPU kernels. The latest release of cuPQC features new primitives, including expanded hash function support and Merkle trees. These additions significantly broaden the range of applications users can develop while enhancing both efficiency and security.

Here’s what’s new in v0.4. 

How cuPQC uses hash functions and Merkle trees

First introduced in cuPQC v0.3 and expanded in the latest release, cuHash provides robust hash function support—now including SHA2, SHA3, SHAKE, and Poseidon2-BabyBear. Another major addition in v0.4 is comprehensive support for Merkle-tree calculations, enabling you to efficiently manage data integrity and verification processes. 

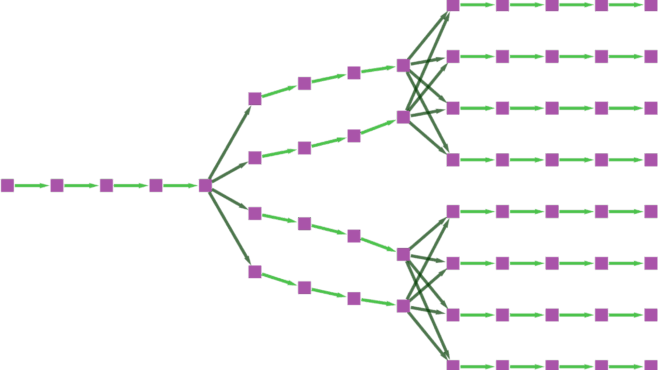
Unlike traditional hash chains that require O(N) time complexity, Merkle trees achieve many applications in O(logN) time. In a binary Merkle tree, each non-leaf node is the hash of its two child nodes, and leaf nodes represent the hash of the input data blocks. For example, if H_A = Hash(Data_A) and H_B = Hash(Data_B), then the parent node H_AB = Hash(H_A || H_B). Once the tree is constructed, it can be used to create a proof for any leaf node. A verifier can use proof nodes with the root node to verify the proof for specific data (see Figure 1). 

To generate a proof for a leaf node (e.g., H_E = Hash(Data_E), the necessary hash nodes required for the proof are the sibling nodes at each level that form the path from the selected node to the root. These sibling nodes are the proof that is used to reconstruct the path to the root, confirming the existence of the selected leaf node in the tree. For example, to generate a proof for the leaf node H_E = Hash(Data_E), the proof sequence would be [H_F,H_GH,H_ABCD] (see Figure 2).

To verify, the verifier starts with the leaf node (e.g., H_E), the known root hash (e.g., H_ABCDEFGH), and the proof sequence (e.g., [H_F,H_GH,H_ABCD]). The verifier then computes the root by sequentially hashing the leaf node with the proof nodes: H^’_ABCDEFGH = Hash( H_ABCD || Hash(Hash(H_E || H_F) || H_GH)). Finally, the verifier compares the computed root with the known root. If the computed root matches the known root (i.e.,  H_ABCDEFGH ==  H^’_ABCDEFGH), the proof is valid (see Figure 3).

With this addition, cuPQC users are now able to:

• Construct binary Merkle trees 
• Generate and verify Merkle proofs to ensure data integrity 
• Optimize storage and improve performance of data verification processes 

cuPQC’s support for a wider range of hash functions and Merkle trees has implications for work across security. Below we give four examples of how these primitives have broad use across cryptographic applications.

Data integrity verification: 

Merkle trees, with their exponential speed-up capabilities, provide a powerful and efficient mechanism for verifying the integrity of large datasets with minimal computation time.

In these systems, data is organized into blocks, each block is hashed, and a Merkle tree is constructed. Any changes in the data can be swiftly detected by recalculating the root hash and comparing it to the original. This ensures the integrity of the data with minimal overhead, making it highly suitable for environments where performance and reliability are paramount.

Membership proofs:

Merkle trees excel at membership proofs, enabling the verification of the presence or absence of an element in a set without exposing the entire dataset. This capability is particularly useful in high security and efficiency scenarios. For example:

• Access control systems: Merkle trees can verify user permissions without revealing the full list of authorized users, thereby enhancing security by minimizing the amount of exposed information.
• Database queries: When querying large databases, Merkle trees can efficiently confirm the existence of a specific record without needing to access or disclose the entire database. This not only improves query performance but also maintains data confidentiality.

Zero-knowledge proofs:

Zero-knowledge proofs (ZKPs) allow one party to prove that they know a value to another party without revealing the information. This powerful cryptographic tool ensures that sensitive information remains private while still enabling verification. By combining hash functions with Merkle tree support, cuPQC enables efficient and secure proof systems for privacy-preserving applications. 

While a variety of hash functions can be employed in the ZKP process, certain constructions use more specialized hash functions like Poseidon—now available in cuPQC v0.4. These hash functions are specifically designed to optimize both performance and security, making them particularly effective in privacy-preserving systems.

Some use cases of ZKPs include: 

• Privacy-focused authentication: Prove a user’s identity without revealing any credentials, significantly reducing the risk of credential theft.
• Secure voting: Maintain voter privacy while proving eligibility to vote, ensuring the integrity and confidentiality of the voting process.
• Confidential transactions: Enable private financial transactions by proving that they meet certain criteria without disclosing the actual details.
• Regulatory compliance: Prove adherence to regulations without exposing sensitive business data, such as verifying financial thresholds have been met without revealing actual financial statements.
• Supply chain verification: Verify the authenticity and integrity of goods without disclosing sensitive supplier or production information.
• Digital ID: Create secure digital identities that allow individuals to prove who they are without revealing personal information, enhancing privacy and security in digital interactions.

Digital signatures:

Hash functions and Merkle trees play a significant role in new post-quantum cryptography (PQC) schemes. As quantum computing poses significant threats to traditional cryptographic algorithms, hash-based signature schemes like XMSS, LMS, and SPHINCS+ have emerged as robust solutions. These schemes leverage the structural integrity of Merkle trees and the cryptographic strength of hash functions to create secure and verifiable signatures. 

In hash-based signatures, it is common to organize public keys into a Merkle tree, where each leaf node represents a unique public key generated through a one-time signature (OTS) scheme. The root hash of the Merkle tree serves as a master public key, providing a compact and efficient means to verify the authenticity of individual signatures.

By accelerating hash-based digital signatures using Merkle trees, cuPQC provides a forward-looking solution for quantum-safe and future-proof cryptographic protocols.

Getting started with cuPQC

You can begin exploring these new features of cuPQC today. Download cuPQC and see how simple it is to start integrating it into your projects, with examples for practical implementations and usage scenarios. Comprehensive documentation offers detailed guides, API references, and troubleshooting tips to help you make the most of cuPQC.