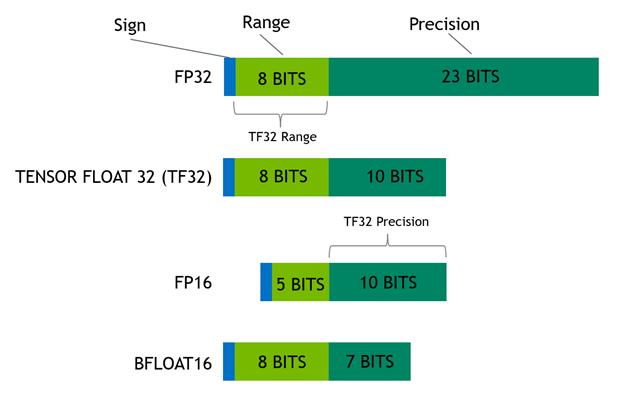
In previous posts on FP8 training, we explored the fundamentals of FP8 precision and took a deep dive into the various scaling recipes for practical large-scale deep learning. If you haven’t read those yet, we recommend starting there for a solid foundation.
This post focuses on what matters most in production: speed. FP8 training promises faster computation, but how much real-world acceleration does it actually deliver? And what are the hidden overhead penalties that might diminish these theoretical gains?
We’ll compare the leading FP8 scaling recipes side by side, using real benchmarks on NVIDIA H100 and NVIDIA DGX B200 GPUs. We rigorously evaluate each FP8 recipe using NVIDIA NeMo Framework—from delayed and current scaling to MXFP8 and generic block scaling—in terms of training efficiency, numerical stability, hardware compatibility, and scalability as model sizes increase.
By examining both convergence behavior and throughput across diverse LLMs, this post provides clear, actionable insights into how each approach performs in practical, demanding scenarios.
Why does speedup matter in FP8 training?
Training LLMs and other state-of-the-art neural networks is an increasingly resource-intensive process, demanding vast computational power, memory, and time. As both model and dataset scales continue to grow, the associated costs—financial, environmental, and temporal—have become a central concern for researchers and practitioners.
FP8 precision directly addresses these challenges by fundamentally improving computational efficiency. By reducing numerical precision from 16 or 32 bits down to just 8 bits, FP8 enables significantly faster computation, which translates directly into accelerated research cycles, reduced infrastructure expenditures, and the unprecedented ability to train larger, more ambitious models on existing hardware.
Beyond raw computational speed, FP8 also critically reduces communication overhead in distributed training environments, as lower-precision activations and gradients mean less data needs to be transferred between GPUs, directly alleviating communication bottlenecks and helping maintain high throughput at scale, an advantage that becomes increasingly vital as model and cluster sizes expand.
What are the strengths and trade-offs of FP8 scaling recipes?
This section briefly recaps the four primary FP8 scaling approaches evaluated in this work, highlighting their unique characteristics. For a deeper dive into the mechanics and implementation details of each recipe, see Per-Tensor and Per-Block Scaling Strategies for Effective FP8 Training.
- Per-tensor delayed scaling: Offers good FP8 computation performance by using a stable, history-derived scaling factor, but its robustness can be impacted by outlier values in the amax history, potentially leading to instabilities and hindering overall training.
- Per-tensor current scaling: Provides high responsiveness and instant adaptation to tensor ranges, leading to improved model convergence and maintaining minimal computational and memory overhead due to its real-time amax calculation and lack of historical tracking.
- Sub-channel (generic block) scaling: Enhances precision and can unlock full FP8 efficiency by allowing configurable block dimensions and finer-grained scaling, though smaller blocks increase scaling factor storage overhead and transpose operations may involve re-computation.
- MXFP8: As a hardware-native solution, this recipe delivers highly efficient block scaling with fixed 32-value blocks for both activations and weights and E8M0 power-of-2 scales, resulting in significant performance gains (up to 2x GEMM throughput) and minimized quantization error through NVIDIA Blackwell accelerated operations.
| Scaling recipe | Speedup | Numerical stability | Granularity | Recommended models | Recommended hardware |
| Delayed scaling | High | Moderate | Per tensor | Small dense models | NVIDIA Hopper |
| Current scaling | High | Good | Per tensor | Medium-sized dense and hybrid models | NVIDIA Hopper |
| Sub-channel scaling | Medium | High | Custom 2D block of 128×128 | MoE models | NVIDIA Hopper and Blackwell |
| MXFP8 | Medium | High | Per 32-value block | All | NVIDIA Blackwell and Grace-Blackwell |
Scaling recipe granularity
Figure 1 shows measured FP8 higher-precision matrix multiplications (GEMM) throughput speedup over BF16 for various scaling approaches on NVIDIA H100. Hardware-native scaling (channel-wise, subchannel-wise, tensor-wise) achieves up to 2x acceleration, underscoring why FP8 is so effective at the hardware level.
While FP8 offers significant speedups over BF16, the choice of scaling granularity; that is, how finely scaling factors are applied within a tensor introduces nuanced trade-offs in actual performance, particularly for GEMM operations. Finer granularity, while beneficial for numerical stability and accuracy by better accommodating intra-tensor variability, can introduce additional overhead that impacts raw throughput.
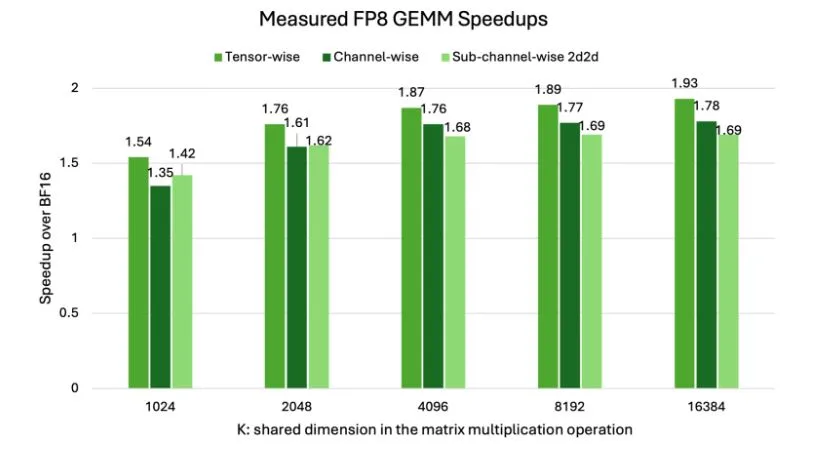
A clear hierarchy in performance is observed when varying scaling granularities for GEMM operations. Tensor-wise scaling generally demonstrates the highest speedup. With only a single scaling factor per entire tensor involved in the GEMM, the overhead associated with scale management is minimized.
Channel-wise scaling represents an intermediate level of granularity, typically applying a scaling factor per channel or a row/column. As seen in the figure, its speedup falls between tensor-wise and 2D block-wise methods.
Sub-channel-wise 2D2D Scaling (for example, with 1×128 for activations and 128×128 blocks for weights) method, representing a finer granularity, generally exhibits slightly lower speedups compared to tensor-wise scaling. The management of multiple scaling factors for the many smaller blocks within a tensor introduces a computational cost that, while crucial for accuracy, can reduce peak raw throughput. This holds true for other configurable block dimensions like 1D1D or 1D2D, where finer block divisions mean more scales to process per GEMM.
Crucially, the x-axis in Figure 1 highlights the impact of GEMM size. As K increases (meaning larger GEMM operations), the overall speedup of FP8 over BF16 generally improves across all scaling methods. This is because for larger GEMMs, the computational savings from using 8-bit precision become more dominant, outweighing the relative overhead of managing scaling factors. In essence, larger GEMMs allow the inherent benefits of FP8 compute to shine through more effectively, even with the added complexity of finer-grained scaling.
While hardware-native solutions like MXFP8 are designed to mitigate the overhead of block scaling through dedicated Tensor Core acceleration, for general FP8 block scaling implementations, the trade-off between granularity (for accuracy) and raw performance remains a key consideration.
Beyond raw speedup, a critical aspect of low-precision training is convergence—how well the model learns and reduces its loss, and ultimately, how it performs on specific downstream tasks. While training loss provides valuable insight into the learning process, it’s important to remember that it’s not the sole metric for FP8 efficacy; robust FP8 downstream evaluation metrics are the ultimate arbiters of a model’s quality.
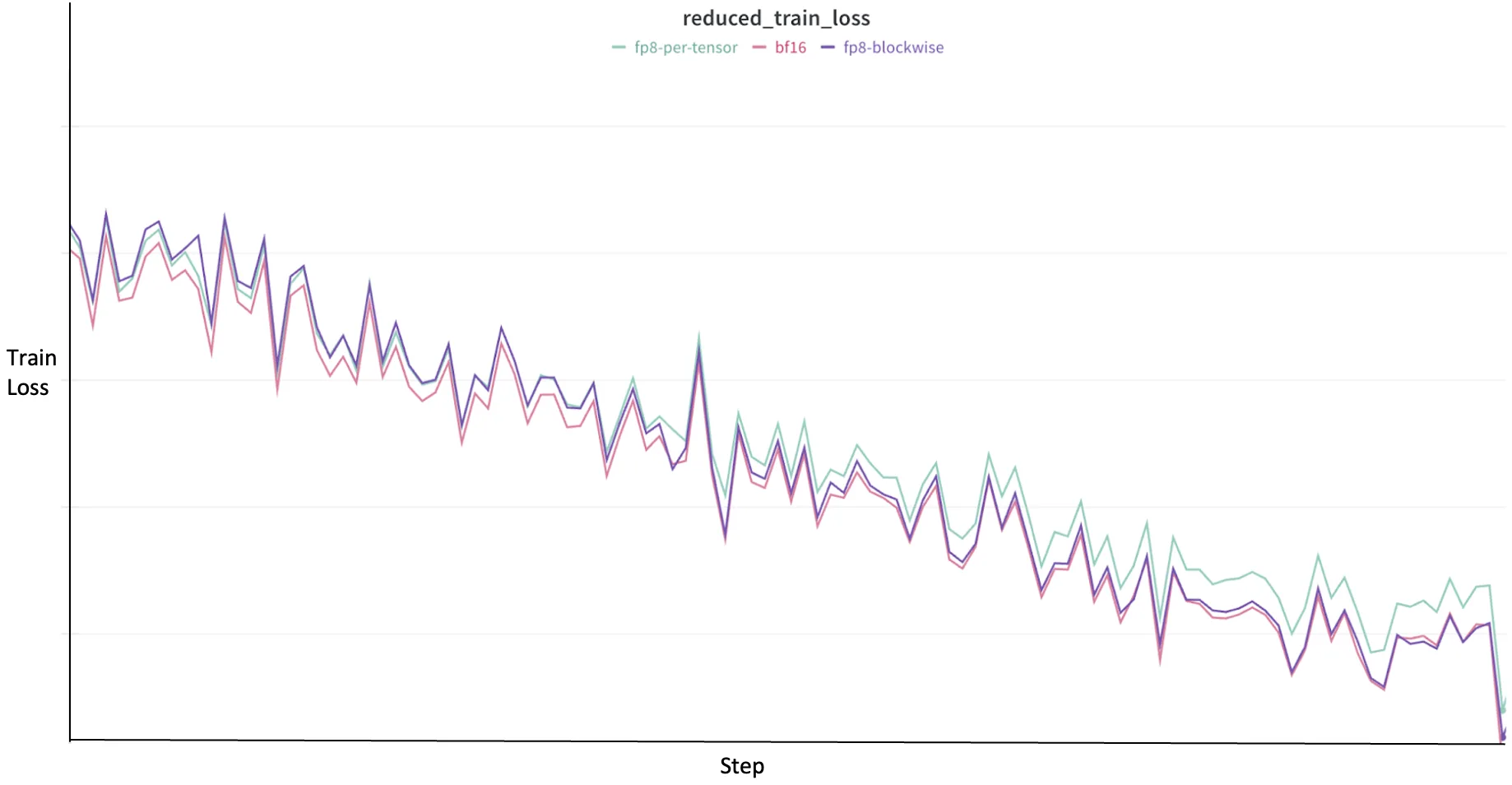
When adopting FP8, the expectation is that the training loss trajectory should closely mirror that of a higher-precision baseline, such as BF16, to ensure that the model is learning effectively without significant degradation. As shown in Figure 2, the training loss trajectories for different scaling strategies relative to BF16. The pink line represents the BF16 baseline. Notably, the dark purple line, representing FP8-blockwise scaling, consistently follows a trajectory very similar to BF16. This close alignment indicates that with finer granularity, block-wise scaling can preserve numerical fidelity more effectively, leading to a convergence behavior that closely matches the higher-precision BF16 training.
Conversely, the light green line, representing FP8-per-tensor scaling, occasionally shows slight deviations or higher fluctuations in loss. This subtle difference in convergence trajectory highlights the trade-off inherent in granularity: while coarser-grained per-tensor scaling might offer higher raw GEMM throughput as discussed previously, finer-grained block-wise scaling tends to yield less accuracy loss and a more stable learning path that closely mirrors BF16.
This illustrates the crucial balance between speedup and numerical stability in FP8 training. More granular scaling methods, by better accommodating the diverse dynamic ranges within tensors, can lead to convergence trajectories that more faithfully track higher-precision baselines, though this might come with a corresponding difference in speed compared to less granular approaches. The optimal choice often involves weighing the demands of downstream evaluation against available computational resources and desired training speed.
Experimental setup
All experiments in this post were conducted using NVIDIA NeMo Framework 25.04, the latest release of the NeMo framework at the time of writing. NeMo Framework 25.04 provides robust, production-grade support for FP8 training through the NVIDIA Transformer Engine (TE), and includes out-of-the-box recipes for dense architectures.
We evaluated two leading FP8 approaches: the current scaling recipe on H100 GPUs and the MXFP8 recipe on the newer NVIDIA DGX B200 architecture. For both, we tested a range of state-of-the-art models, including Llama 3 8B, Llama 3 70B, Llama 3.1 405B, Nemotron 15B, and Nemotron 340B. Each setup was compared directly against a BF16 baseline to measure the practical speedup delivered by FP8 in real-world training scenarios.
Current scaling recipe
As illustrated in Figure 3, the current scaling FP8 recipe on H100 GPUs demonstrates a pronounced, model-size-dependent speedup when compared to the BF16 baseline. For smaller models such as Llama3 8B, the speedup is approximately 1.30x.
This advantage becomes even more significant with larger architectures. For example, the Llama 3 70B model achieves a speedup of 1.43x, and the largest model in our benchmark suite, Llama 3.1 405B, reaches an impressive 1.53x acceleration.
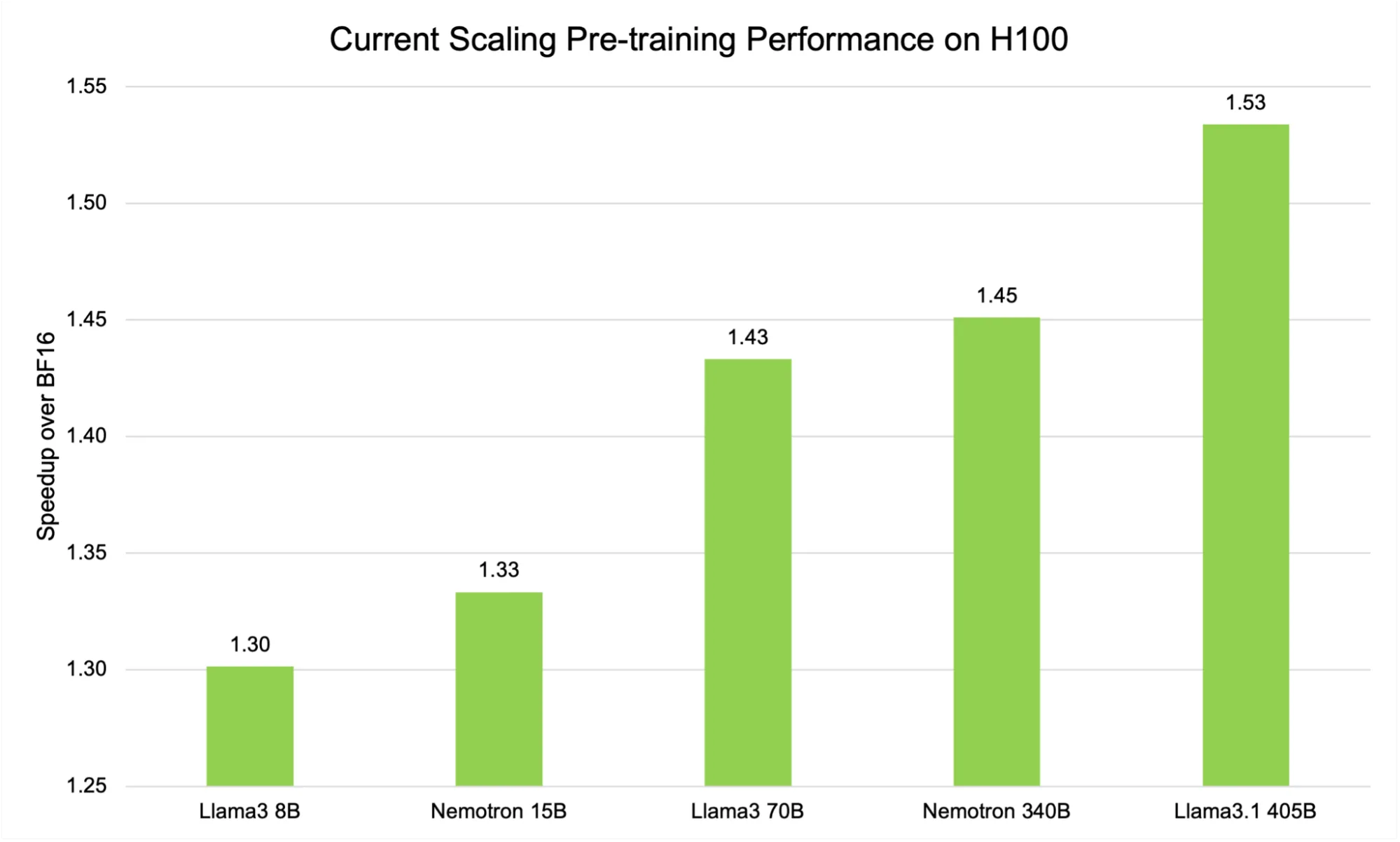
This upward trend is not just a statistical curiosity—it underscores a fundamental advantage of FP8 training for large-scale language models. As model size and computational complexity increase, the efficiency gains from reduced-precision arithmetic become more pronounced.
The reason is twofold: First, larger models naturally involve more matrix multiplications and data movement, both of which benefit substantially from the reduced memory footprint and higher throughput of FP8 on modern hardware. Second, the overheads associated with scaling and dynamic range adjustments become relatively less significant as the total computation grows, allowing the raw performance benefits of FP8 to dominate.
MXFP8 recipe
Figure 4 shows the performance of the MXFP8 recipe on DGX B200 GPUs, revealing a consistent speedup over BF16 across different model sizes, with observed gains ranging from 1.28x to 1.37x. While these absolute speedup values are slightly lower than those achieved by the current scaling recipe, they are notable for their stability and reliability across a diverse set of models.

The relative flatness in speedup from 8B to 70B parameters—contrasted with the higher jump at 340B—reflects how block-based scaling interacts with model and hardware characteristics. MXFP8 assigns a shared scaling factor to each 32-element block, which can introduce additional memory access overhead for mid-sized models. However, as model size increases and computation becomes the dominant bottleneck (as seen with Nemotron 340B), the efficiency benefits of block-wise FP8 become more pronounced, leading to the observed peak speedup.
These results highlight the architectural strengths of the Blackwell (B200) platform, whose Tensor Cores and memory hierarchy are optimized for microscaling formats like MXFP8. This enables high throughput and stable convergence, even as models scale into the hundreds of billions of parameters. The block-level scaling approach of MXFP8 effectively balances dynamic range and computational efficiency, delivering reliable acceleration while mitigating risks of numerical instability.
This consistency reflects the architectural advancements of NVIDIA Blackwell architecture, which was purpose-built to maximize efficiency for lower-precision formats like FP8 and, specifically, for block-based scaling approaches such as MXFP8. The B200 Tensor Cores and advanced memory hierarchy are optimized for these microscaling formats, enabling high throughput and efficient memory utilization even as model sizes continue to increase. With MXFP8, each block of 32 values shares a scaling factor, striking a balance between dynamic range and computational efficiency. This approach allows for robust acceleration while minimizing the risk of numerical instability—a key consideration when pushing models to ever-larger scales.
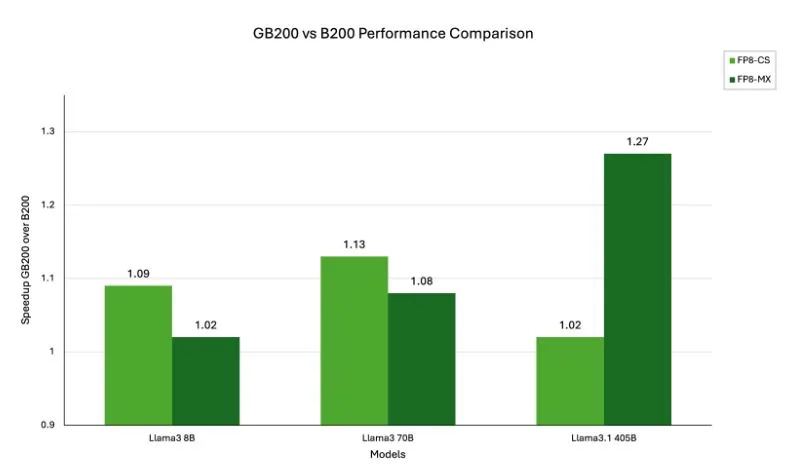
How does NVIDIA GB200 Grace Blackwell Superchip compare to NVIDIA Blackwell architecture?
The comparison between GB200 and B200 highlights how architectural integration and system design can translate into tangible performance gains for large-scale AI workloads. Both are built on NVIDIA Blackwell architecture, but the GB200 superchip combines two B200 GPUs with a Grace CPU, interconnected through NVIDIA NVLink, resulting in a unified memory domain and exceptionally high memory bandwidth.
Get started with practical FP8 training
A clear pattern emerges from these benchmarks: for dense models, the bigger the model, the bigger the speedup with FP8. This is because as model size increases, the number of matrix multiplications (GEMMs) grows rapidly, and these operations benefit most from the reduced precision and higher throughput of FP8. In large dense models, FP8 enables dramatic efficiency gains, making it possible to train and fine-tune ever-larger language models with less time and compute.
These empirical results reinforce the specific strengths and tradeoffs of each FP8 scaling recipe detailed in this post and demonstrate that both per-tensor and MXFP8 approaches deliver significant speedup and convergence benefits over BF16.
Ready to try these techniques yourself? Explore the FP8 recipes to get started with practical FP8 training configurations and code.