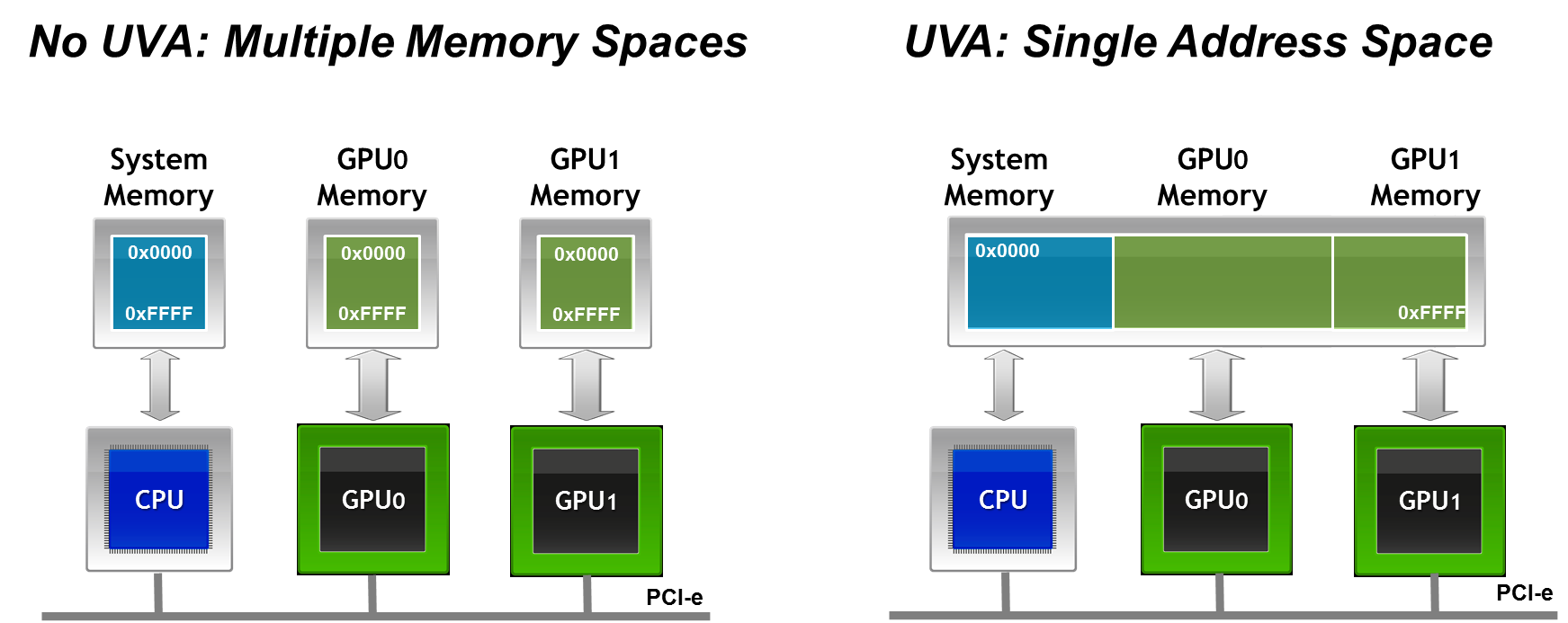
I introduced CUDA-aware MPI in my last post, with an introduction to MPI and a description of the functionality and benefits of CUDA-aware MPI. In this post I will demonstrate the performance of MPI through both synthetic and realistic benchmarks.
Synthetic MPI Benchmark results
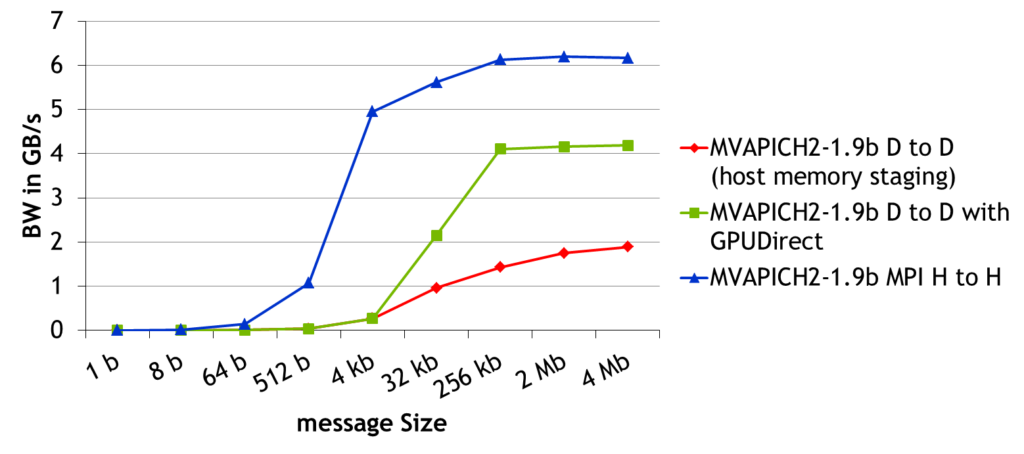
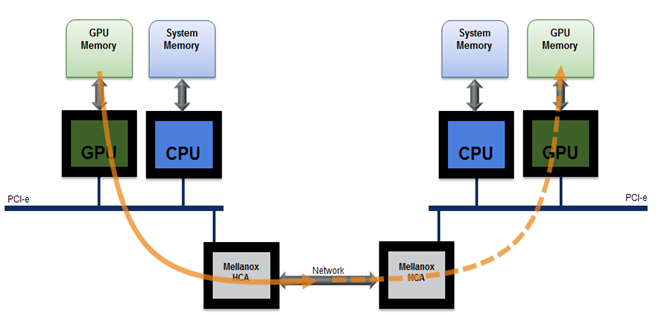
Since you now know why CUDA-aware MPI is more efficient from a theoretical perspective, let’s take a look at the results of MPI bandwidth and latency benchmarks. These benchmarks measure the run time for sending messages of increasing size from a buffer associated with MPI rank 0 to a buffer associated with MPI rank 1. Using MVAPICH2-1.9b I have measured the following bandwidths and latencies between two Tesla K20 GPUs installed in two nodes connected with FDR infiniband. I have included host-to-host MPI bandwidth results as a reference. The measured latencies for 1 byte messages are 19 microseconds for regular MPI, 18 microseconds for CUDA-aware MPI with GPUDirect accelerated communication with network and storage devices, and 1 microsecond for host-to-host communication. The peak bandwidths for the 3 cases are 6.19 GB/s for host-to-host transfers, 4.18 GB/s for device-to-device transfers with MVAPICH2-1.9b and GPUDirect, and 1.89 GB/s for device-to-device transfers with staging through host memory.
A real world example: CUDA+MPI Jacobi with CUDA-aware MPI
Let’s use the Jacobi solver already covered in other blog posts (An OpenACC Example (Part 1), An OpenACC Example (Part 2)) as a real world example. It solves the Poisson equation on a rectangle with Dirichlet boundary conditions. You can download the Jacobi solver source code from github.
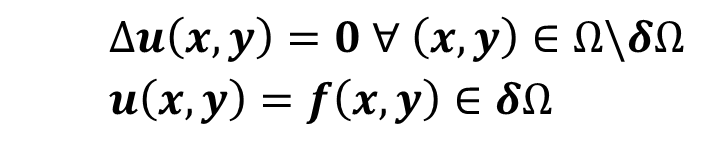
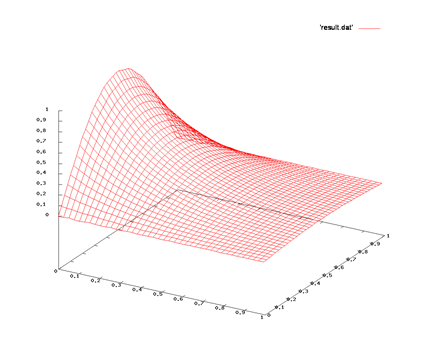
We apply the following algorithm to solve the Poisson equation with a Jacobi solver.
while ( iterations < JACOBI_MAX_LOOPS && residue > JACOBI_TOLERANCE )
{
residue = CallJacobiKernel();
// Exchange the A and Anew
SwapSolution();
if ( iterations % 100 == 0 )
printf( "Iteration: %d - Residue: %.6fn", iterations, residue );
++iterations;
}
We use second-order central differences to approximate the Laplacian operator on our discrete grid. The Jacobi kernel applies the following update to every inner point of our domain.
Anew[j][i] = 0.25f * ( A[j][i+1]
+ A[j-1][i] + A[j+1][i]
+ A[j][i-1]);
To use multiple GPUs in multiple nodes we apply a 2D domain decomposition with n × k domains. We have chosen a 2D domain decomposition to reduce the amount of data transferred between processes compared to the required computation. With a 1D domain decomposition the communication would become more and more dominant as we add GPUs.
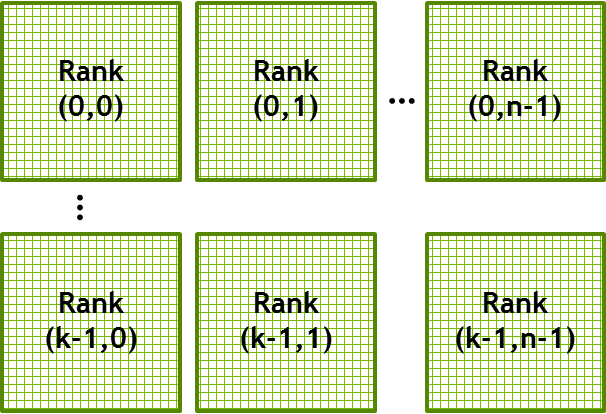
When applying the domain decomposition it is also necessary to exchange data between the GPUs that cooperatively solve the problem. For this we use halo cells which we must update after every iteration. We do not need to change the kernel but we do need to extend our algorithm to include the communication step.
while ( iterations < JACOBI_MAX_LOOPS && residue > JACOBI_TOLERANCE )
{
residue = CallJacobiKernel();
// Exchange the A and Anew
SwapSolution();
// Send and receive halo (exchange) elements
TransferAllHalos();
if ( iterations % 100 == 0 )
printf( "Iteration: %d - Residue: %.6fn", iterations, residue );
++iterations;
}

To do the halo exchange we use the following MPI code.
//exchange top and bottom
MPI_Sendrecv(devSendTop, elemCount, MPI_DOUBLE, topneighbor, 100,
devRecvTop, elemCount, MPI_DOUBLE, topneighbor, 100, MPI_COMM_WORLD, &status);
MPI_Sendrecv(devSendBottom, elemCount, MPI_DOUBLE, bottomneighbor, 100,
devRecvBottom, elemCount, MPI_DOUBLE, bottomneighbor, 100, MPI_COMM_WORLD, &status);
//exchange left and right
GatherLeftAndRightBorders();
MPI_Sendrecv(devSendLeft, elemCount, MPI_DOUBLE, leftneighbor, 100,
devRecvLeft, elemCount, MPI_DOUBLE, leftneighbor, 100, MPI_COMM_WORLD, &status);
MPI_Sendrecv(devSendRight, elemCount, MPI_DOUBLE, rightneighbor, 100,
devRecvRight, elemCount, MPI_DOUBLE, rightneighbor, 100, MPI_COMM_WORLD, &status);
ScatterLeftAndRightBorders();
For simplicity, I have omitted from the above the code to handle the corner cases where a process does not have a top, bottom, left, or right neighbor. The complete code, available on github, uses MPI virtual topologies to make use of nearest neighbor networks like the 3D torus in a Cray XK7. The gather and scatter operations are needed because the cells that need to be exchanged with the left and right neighbors are not contiguous in memory so they need to be gathered into, or scattered out of a contiguous array to be able to do a single call to MPI_Sendrecv instead of many calls to MPI_Sendrecv, each sending a small amount of data. This is much more efficient.
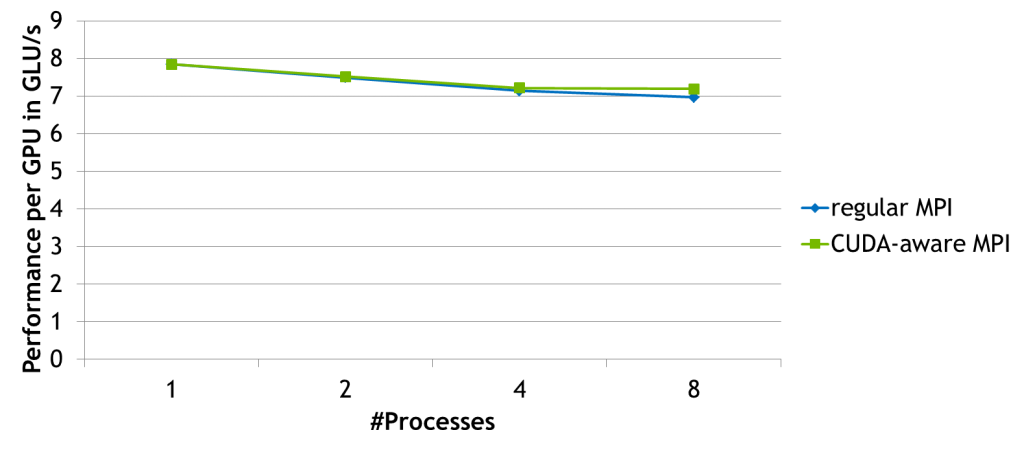
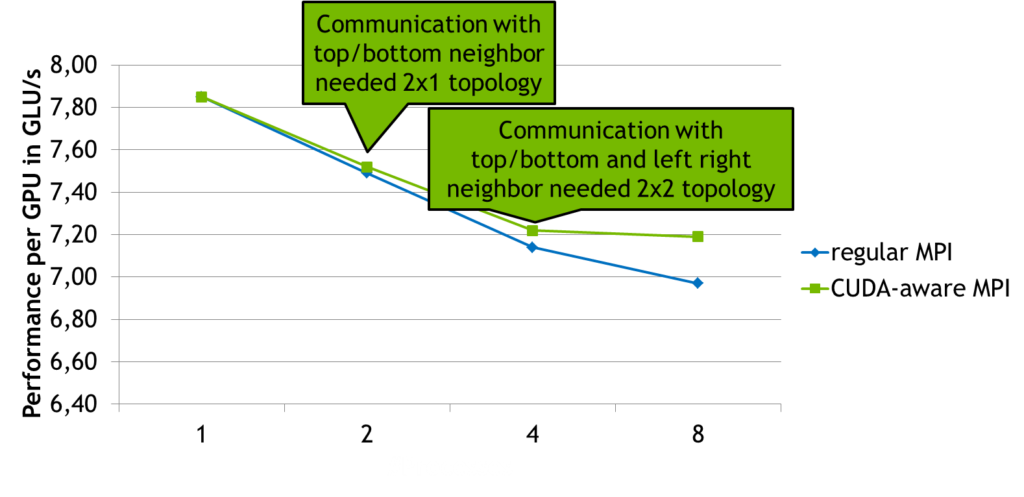
I performed a weak scaling experiment with this code on a 4-node cluster, where every node houses two Tesla K20 GPUs and the nodes are connected with FDR infiniband. For this weak scaling problem I increase the domain size as more and more GPUs are added, so that each GPU always works on a 4k by 4k domain. This way linear (optimal) scaling would imply that the achieved performance per GPU should remain constant. As the code is not very communication intensive we see that both the regular MPI version as well as the CUDA-aware MPI version scale quite well with the advantage of the CUDA-aware version growing as the amount of communication increases when more GPUs are added.
If we zoom in we can see that the performance decreases at two points.
- When going from 1 to 2 processes. This is due to the communication between the top and bottom neighbors that is now necessary.
- When going from 2 to 4 processes. This is due to the communication between the left and right neighbors, which also includes the required gather and scatter operations.
Going from 4 to 8 processes the CUDA-aware MPI version scales nearly optimally while the non-CUDA-aware version continues to lose some performance due to slower communication. When reasoning about these results please keep in mind that the overall execution time is not dominated by communication. I chose a weak scaling benchmark with a communication-reducing 2D domain decomposition to avoid constructing an artificial benchmark just to show off CUDA-aware MPI. For the same reason I chose a domain size of 4k by 4k because this problem size demonstrates strong performance in the single-GPU version. Even in this scenario CUDA-aware MPI shows a performance advantage over regular MPI even on a small number of nodes.
I’ll finish this post with a few tips related to the usage of CUDA-aware MPI.
CUDA-aware MPI and OpenACC
To use MPI with OpenACC you can use the update directive to stage GPU buffers through host memory.
#pragma acc update host(s_buf[0:size]) MPI_Send(s_buf,size,MPI_CHAR,1,100,MPI_COMM_WORLD);
With CUDA-aware MPI it is more efficient to get the device pointer of your array with the host_data directive, which benefits from optimized transfers in the CUDA-aware MPI implementation.
#pragma acc host_data use_device(s_buf) MPI_Send(s_buf,size,MPI_CHAR,1,100,MPI_COMM_WORLD);
CUDA-aware MPI Remarks
Several commercial and open-source CUDA-aware MPI implementation are available.
- MVAPICH2 (since version 1.8)
- OpenMPI (since version 1.8)
- CRAY MPI (since MPT 5.6.2)
- IBM Platform MPI (since version 8.3)
A CUDA-aware MPI implementation needs some internal data structures associated with a CUDA context. Depending on the implementation these data structures might get allocated in MPI_Init (e.g. for MVAPICH2 up to version 1.9) or lazily at a later point (e.g. for OpenMPI or MVAPICH2 2.0 or later). For the MPI implementations setting things up in MPI_Init you need to call cudaSetDevice before MPI_Init to ensure that the same GPU is chosen by MPI and your application code. To explicitly handle GPU affinity you can use MPI environment variables:
MV2_COMM_WORLD_LOCAL_RANKfor MVAPICH2, orOMPI_COMM_WORLD_LOCAL_RANKfor OpenMPI.
You should ensure that CUDA functionality is enabled at run time for the CUDA-aware MPI implementation you are using. For MVAPICH2, Cray MPT, and IBM Platform MPI the following environment variables should be set.
MV2_USE_CUDAfor MVAPICHMPICH_RDMA_ENABLED_CUDAfor Cray MPTPMPI_GPU_AWAREfor Platform MPI
Conclusions
CUDA-aware MPI provides important performance benefits for CUDA applications on clusters, including
- ease of use;
- pipelined data transfers that automatically provide optimizations when available, including overlap of CUDA copy and RDMA transfers, and utilization of the best GPUDirect technology available.
The source code of the Jacobi Solver can be downloaded from Github.