Voting and Shuffling to Optimize Atomic Operations

2iSome years ago I started work on my first CUDA implementation of the Multiparticle Collision Dynamics (MPC) algorithm, a particle-in-cell code used to simulate hydrodynamic interactions between solvents and solutes. As part of this algorithm, a number of particle parameters are summed to calculate certain cell parameters. This was in the days of the Tesla GPU architecture (such as GT200 GPUs, Compute Capability 1.x), which had poor atomic operation performance. A linked list approach I developed worked well on Tesla and Fermi as an alternative to atomic adds but performed poorly on Kepler GPUs. However, atomic operations are much faster on the Kepler and Maxwell architectures, so it makes sense to use atomic adds.

These types of summations are not limited to MPC or particle-in-cell codes, but, to some extent, occur whenever data elements are aggregated by key. For data elements sorted and combined by key with a large number of possible values, pre-combining elements with the same key at warp level can lead to a significant speed-up. In this post, I will describe algorithms for speeding up your summations (or similar aggregations) for problems with a large number of keys where there is a reasonable correlation between the thread index and the key. This is usually the case for elements that are at least partially sorted. Unfortunately, this argument works in both directions: these algorithms are not for you if your number of keys is small or your distribution of keys is random.  To clarify: by a “large” number of keys I mean more than could be handled if all bins were put into shared memory.

Note that this technique is related to a previously posted technique called warp-aggregated atomics by Andrey Adinetz, and also to the post Fast Histograms Using Shared Atomics on Maxwell by Nikolay Sakharnykh. The main difference here is that we are aggregating many groups, each designated by a key (to compute a histogram, for example). So you could consider this technique “warp-aggregated atomic reduction by key”.

Double Precision Atomics and Warp Divergence

To achieve sufficient numerical precision, the natively provided single-precision atomicAdd is often inadequate. Unfortunately, using the atomicCAS loop to implement double precision atomic operations (as suggested in the CUDA C Programming guide) introduces warp divergence, especially when the order of the data elements correlates with their keys. However, there is a way to remove this warp divergence (and a number of atomic operations): pre-combine all the elements in each warp that share the same key and use only one atomic operation per key and warp.

Why Work With Warps?

Using a “per warp” approach has two practical benefits. First, thread in a warp can communicate efficiently using warp vote and __shfl (shuffle) operations. Second, there is no need for synchronization because threads in a warp work synchronously.

Applying the concepts shown later at the thread block level is significantly slower because of the slower communication through shared memory and the necessary synchronization.

Finding Groups of Keys Within a Warp

Various algorithms can be used to find the elements in a warp that share the same key (“peers”). A simple way is to loop over all different keys, but there are also hash-value based approaches using shared memory and probably many others. The performance and sometimes also the suitability of each algorithm depends on the type and distribution of the keys and the architecture of the target GPU.

The code shown in example 1 should work with keys of all types on Kepler and later GPUs (Compute Capability 3.0 and later). It takes the key of lane 0 as reference, distributes it using a __shfl() operation to all other lanes and uses a __ballot() operation to determine which lanes share the same key. These are removed from the pool of lanes and the procedure is repeated with the key of the first remaining lane until all keys in the warp are checked. For each warp, this loop obviously has as many operations as there are different keys. The function returns a bit pattern for each thread with the bits of its peer elements set. You can see a step-by-step example of how this works starting on slide 9 of my GTC 2015 talk.

template<typename G>
__device__ __inline__ uint get_peers(G key) {
    uint peers=0;
    bool is_peer;

    // in the beginning, all lanes are available
    uint unclaimed=0xffffffff;

    do {
        // fetch key of first unclaimed lane and compare with this key
        is_peer = (key == __shfl(key, __ffs(unclaimed) - 1));

        // determine which lanes had a match
        peers = __ballot(is_peer);

        // remove lanes with matching keys from the pool
        unclaimed ^= peers;

        // quit if we had a match
    } while (!is_peer);

    return peers;
}

Pre-Combining Peers

Ideally, the peer elements found can be added or otherwise combined in parallel in log₂(max_n_peer) iterations if we use parallel tree-like reductions on all groups of peers. But with a number of interleaved trees traversed in parallel and only represented by bit patterns, it is not obvious which element should be added. There are at least two solutions to this problem:

1. make it obvious by switching the positions of all elements back and forth for the calculation; or
2. interpret the bit pattern to determine which element to add next.

The latter approach had a slight edge in performance in my implementation.

Note that Mark Harris taught us a long time ago to start reductions with the “far away” elements to avoid bank conflicts. This is still true when using shared memory, but with the __shfl() operations used here, we do not have bank conflicts, so we can start with our neighboring peers. (See the post “Faster Reductions on Kepler using SHFL”).

Parallel Reductions

Let’s start with some observations on the usual parallel reductions. Of the two elements combined in each operation, the one with the higher index is used and, therefore, obsolete. At each iteration, every second remaining element is “reduced away”. In other words, in iteration i (0 always being the first here), all elements with an index not divisible by 2ⁱ⁺¹ are “reduced away”, which is equivalent to saying that in iteration i, elements are reduced away if the least-significant bit of their relative index is 2ⁱ.

Replacing thread lane index by a relative index among the thread’s peers, we can perform the parallel reductions over the peer groups as follows.

• Calculate each thread’s relative index within its peer group.
• Ignore all peer elements in the warp with a relative index lower or equal to this lane’s index.
• If the least-significant bit of the relative index of the thread is not 2ⁱ (with i being the iteration), and there are peers with higher relative indices left, acquire and use data from the next highest peer.
• If the least-significant bit of the relative index of the thread is 2ⁱ, remove the bit for the lane of this thread from the bit set of remaining peers.
• Continue until there are no more remaining peers in the warp.

The last step may sound ineffective, but no thread in this warp will continue before the last thread is done. Furthermore, we need a more complex loop exit condition, so there’s no gain in a more efficient-looking implementation.

You can see an actual implementation in Example 2 and a step-by-step walkthrough starting on slide 19 of my GTC 2015 presentation.

template <typename F>
__device__ __inline__ F reduce_peers(uint peers, F &x) {
    int lane = TX&31;

    // find the peer with lowest lane index
    int first = __ffs(peers)-1;

    // calculate own relative position among peers
    int rel_pos = __popc(peers << (32 - lane));

    // ignore peers with lower (or same) lane index
    peers &= (0xfffffffe << lane);

    while(__any(peers)) {
        // find next-highest remaining peer
        int next = __ffs(peers);

        // __shfl() only works if both threads participate, so we always do.
        F t = __shfl(x, next - 1);

        // only add if there was anything to add
        if (next) x += t;

        // all lanes with their least significant index bit set are done
        uint done = rel_pos & 1;

        // remove all peers that are already done
        peers & = ~__ballot(done);

        // abuse relative position as iteration counter
        rel_pos >>= 1;
    }

    // distribute final result to all peers (optional)
    F res = __shfl(x, first);

    return res;
}

Performance Tests

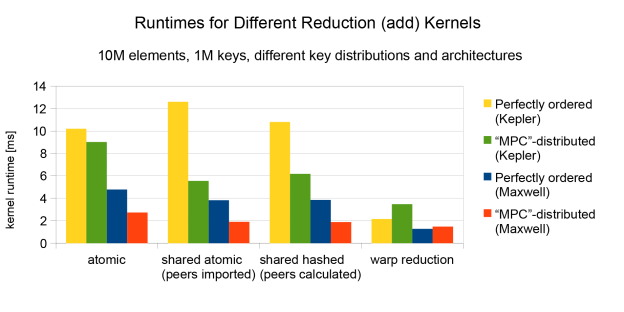
To test the performance I set up an example with a simulation box of size 100x100x100 cells with 10 particles per cell and the polynomial cell index being the key element. This leads to one million different keys and is therefore unsuitable for direct binning in shared memory. I compared my algorithm (“warp reduction” in Figure 1) against an unoptimized atomic implementation and a binning algorithm using shared memory atomics with a hashing function to calculate bin indices per block on the fly.

For comparison I used three different distributions of keys:

• completely random;
• completely ordered by key;
• ordered, then shifted with a 50% probability to the next cell in each direction. This is a test pattern resembling a common distribution during the MPC algorithm.

Tests were performed using single- and double-precision values. For single-precision numbers, the simple atomic implementation is always either faster or at least not significantly slower than other implementations. This is also true for double-precision numbers with randomly distributed keys, where any attempt to reduce work occasionally results in huge overhead. For these reasons single-precision numbers and completely randomly distributed keys are excluded in the comparison. Also excluded is the time used to calculate the peer bit masks, because it varies from an insignificant few percent (shared memory hashing for positive integer keys on Maxwell) to about the same order of magnitude as a reduction step (external loop as described above for arbitrary types, also on Maxwell). But even in the latter case we can achieve a net gain if it is possible to reuse the bit patterns at least once.

Conclusion

For data elements sorted and combined by key with a large number of possible values, pre-combining same-key elements at warp level can lead to a significant speed-up. The actual gain depends on many factors like GPU architecture, number and type of data elements and keys, and re-usability. The changes in code are minor, so you should try it if you have a task fitting the criteria.

For related techniques, be sure to check out the posts Warp-Aggregated Atomics by Andrey Adinetz, and Fast Histograms Using Shared Atomics on Maxwell by Nikolay Sakharnykh.