The Solvency II EU Directive came into effect at the beginning of the year. It harmonizes insurance regulation in the European Union with an economic and risk based approach, which considers the full balance sheet of insurers and re-insurers. In the case of life insurers and pension funds, this requires the calculation of the economic value of the liabilities—the contractual commitments the company has to meet—for long term contracts.
Calculating the economic value of the liabilities and capturing the dependence of the liabilities to different scenarios such as movements of the interest rate or changes of mortality cannot be achieved without detailed models of the underlying contracts and requires a significant computational effort.
A Perfect GPU Use Case
 The calculations have to be executed for millions of pension and life insurance contracts and have to be performed for thousands of interest rate and mortality scenarios. Because of the level of parallelism, this is an excellent case for the application of GPUs and GPU clusters. In addition, variations in the products have to be captured. While implementing a separate code for many products is possible, a lot can be gained from abstractions at a higher level.
The calculations have to be executed for millions of pension and life insurance contracts and have to be performed for thousands of interest rate and mortality scenarios. Because of the level of parallelism, this is an excellent case for the application of GPUs and GPU clusters. In addition, variations in the products have to be captured. While implementing a separate code for many products is possible, a lot can be gained from abstractions at a higher level.
To solve these problem, we use the following technologies.
- The Actulus Modeling Language (AML), a domain specific language for actuarial modeling;
- Alea GPU, QuantAlea’s high performance GPU compiler for .NET C# and F#. See this previous post on Alea GPU;
- The modern functional-first programming language F#.
Armed with these technologies, we can significantly improve the level of abstraction and increase generality. Our system will allow actuaries to be more productive and to harness the power of GPUs without any GPU coding. The performance gain of GPU computing makes it much more practical and attractive to use proper stochastic models and to experiment with a large and diverse set of risk scenarios.
The Actulus Modeling Language
The Actulus Modeling Language (AML) is a domain-specific language for rapid prototyping in which actuaries can describe life-based pension and life insurance products, and computations on them. The idea is to write declarative AML product descriptions and from these automatically generate high-performance calculation kernels to compute reserves and cash flows under given interest rate curves and mortality curves and shocks to these.
AML allows a formalized and declarative description of life insurance and pension products. Its notation is based on actuarial theory and reflects a high-level view of products and reserve calculations. This has multiple benefits:
- The specification of life insurance products and risk models can be handled by actuaries without programming background.
- A uniform language for product description can guarantee coherence across the entire life insurance company.
- Rapid experiments with product designs allow faster and less expensive development of new pension products.
- The same product description can be used for prototyping and subsequent administration, reporting to tax authorities and auditors, solvency computations, etc.
- The DSL facilitates the construction of tools for automated detection of errors and inconsistencies in the design of insurance products.
- Reserve calculations can be optimized automatically for given target hardware, such as GPUs, via code generation.
- Auditors and regulatory bodies such as financial services authorities can benefit from a formalization of products that is
independent of the low-level software concerns of administration, efficient computations, and so on. - Products and risk models are independent of the technology on which computations are executed. Since pensions contracts are extremely long-lived—a contract entered with a 25-year old woman today is very likely to still be in force in 2080—this isolation from technology is very useful.
Actuarial Modeling
The AML system is based on continuous-time Markov models for life insurance and pension products. A continuous-time Markov model consists of a finite number of states and transition intensities between these states. The transition intensity from state
to state
at time
, when integrated over a time interval, gives the transition probability from state
to state
during the time interval. The Markov property states that future transitions depend on the past only through the current state.
Life insurance products are modeled by identifying states in a Markov model and by attaching payment intensities to the states and lump-sum payments
to the transitions.
As an example we consider a product that offers disability insurance. The product can be modeled with three states: active labor market participation, disability, and death. There are transitions from active participation to disability and to death, and from disability to death. Another example is a collective spouse annuity product with future expected cashflows represented by a seven-state Markov model as Figure 1 shows.

Additionally, some products may allow for reactivation, where a previously disabled customer begins active labor again. The product pays a temporary life annuity with repeated payments to the policy holder until some expiration date , provided that he or she is alive. The disability sum pays a lump sum when the policy holder is declared unable to work prior to some expiration
.
Reserves and Thiele’s Differential Equations
The state-wise reserve is the reserve at time
given that the insured is in state
at that time. It is the expected net present value at time
of future payments of the product, given that the insured is in state
at time
. The principle of equivalence states that the reserves at the beginning of the product should be zero, or the expected premiums should equal the expected benefits over the lifetime of the contract.
The state-wise reserves can be computed using Thiele’s differential equation
where is the interest rate at time
. Note that the parameters can be divided into three categories: those that come from a product (
and
), those that come from a risk model (
) and the market variables (
).
Traditionally, it has often been possible to obtain closed-form solutions to Thiele’s differential equations and then use tabulations of the results. With the more flexible products expressible in AML, closed-form solutions are in general not possible. In particular, by allowing reactivation from disability to active labor market participation mentioned above, one obtains a Markov model with a cycle, and in general this precludes closed-form solutions.
Solving Thiele’s Differential Equations
Good numerical solutions of Thiele’s differential equations can be obtained using a 4th-order Runge-Kutta (RK4) solver. A reserve computation typically starts with the boundary condition that the reserve is zero (no payments or benefits) after the insured’s age is 120 years, when he or she is assumed to be dead. Then the differential equations are solved, and the reserves computed, backwards from age 120 to the insured’s current age in fixed time steps.
Here is a code fragment of the inner loops of a simplistic RK4 solver expressed in C#.
for (int y=a; y>b; y--) {
double[] v = result[y-b];
v = daxpy(1.0, v, bj_ii(y));
double t = y;
for (int s=0; s<steps; s++) { // Integrate backwards over [y,y-1]
double[] k1 = dax(h, dV(t, v));
double[] k2 = dax(h, dV(t + h/2, daxpy(0.5, k1, v)));
double[] k3 = dax(h, dV(t + h/2, daxpy(0.5, k2, v)));
double[] k4 = dax(h, dV(t + h, daxpy(1.0, k3, v)));
v = daxpy(1/6.0, k1, daxpy(2/6.0, k2, daxpy(2/6.0, k3, daxpy(1/6.0, k4, v))));
t += h;
}
Array.Copy(v, result[y-1-b], v.Length);
}
It computes and stores the annual reserve backwards from y = a = 120 to y = b = 35, where dV is an array-valued function expressing the right-hand sides of Thiele’s differential equations, and h is the within-year step size, typically between 1 and 0.01.
Solving Thiele’s Equations on GPUs
The computations in the Runge-Kutta code have to be performed sequentially for each contract, consisting of the products relating to a single insured life. However, it is easily parallelized over a portfolio of contracts, of which there are typically hundreds of thousands, one for each customer. Thus, reserve and cash flow computations present an excellent use case for GPUs. Using GPUs for reserve or cash-flow computations is highly relevant in practice, because such computations can take dozens or hundreds of CPU hours for a reasonable portfolio size. Even with cloud computing this results in slow turnaround times; GPU computing could make it much more practical and attractive to use proper stochastic models and to experiment with risk scenarios.
The Runge-Kutta 4 solver fits the GPU architecture very well because it uses fixed step sizes and therefore causes little thread divergence provided the contracts are sorted suitably before the computations are started. By contrast adaptive-step solvers such as the Runge-Kutta-Fehlberg 4/5 or Dormand-Prince are often faster on CPUs. They are more likely to cause thread divergence on GPUs because different input data will lead to iteration counts in the inner loop. Moreover, the adaptive-step solvers deal poorly with the frequent discontinuities in the derivatives that appear in typical pension products, which require repeatedly stopping and then restarting the solver to avoid a deterioration of the convergence rate.
In preliminary experiments, we have obtained very good performance on the GPU over a CPU-based implementation. For instance, we can compute ten thousand reserves for even the most complex insurance products in a few minutes. The hardware we use is an NVIDIA Tesla K40 GPU (Kepler GK110 architecture). The software is a rather straightforward implementation of the Runge-Kutta fixed-step solver, using double-precision (64-bit) floating-point arithmetic. The kernels are written, or in some experiments automatically generated, in the functional language F#, and compiled and run on the GPU using the Alea GPU framework.
The F# language is widely used in the financial industry, along with other functional languages. We use it for several reasons:
- It provides added type safety and convenience in GPU programming compared to C.
- F# is an ideal language for writing program generators, such as generating problem-specific GPU kernels from AML product descriptions.
- The project’s commercial partner uses the .NET platform for all development work, and F# fits well with that ecosystem.
For these reasons the Actulus project selected Quantalea’s Alea GPU platform to develop our GPU code. We find that the Alea GPU platform offers excellent performance and robustness. An additional benefit of Alea GPU is its cross platform capability: the same assemblies can execute on Windows, Linux and Mac OS X.
The chief performance-related problems in GPU programming are the usual ones: How to lay out data (for instance, time-dependent interest rate curves and mortality rates) in GPU memory for coalesced memory access; whether to pre-interpolate or not in such time-indexed tables; how to balance occupancy, thread count and GPU register usage per thread; and so on. Alea GPU is feature complete so that we can implement all the required optimizations to tune the code for maximal
performance.
Figure 2 shows the number of products processed per second as a function of the batch size, i.e., the number of products computed at the same time.
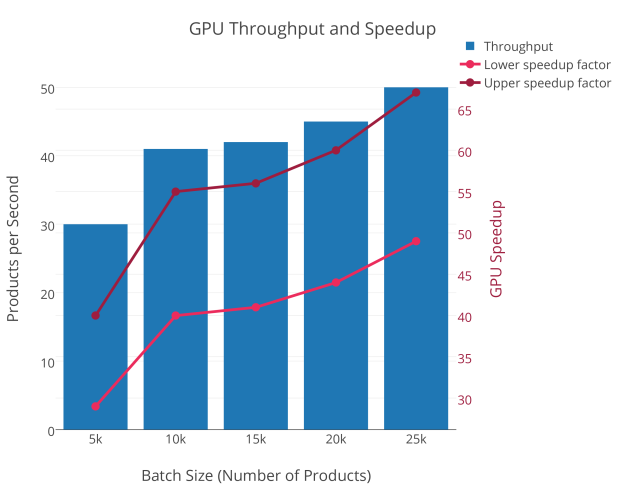
The product in question is a collective spouse annuity product with future expected cashflows calculated for a 30-year-old insured represented by the seven-state Markov model depicted in Figure 1. This product is among the most complex to work with. Depending on the modeling details, the current CPU-based production code, running on a single core at 3.4 GHz, can process between 0.75 and 1.03 collective spouse annuity insurance products per second. If we compare this with the GPU throughput of 30 to 50 insurance products per second we arrive at a speed-up factor in the range of 30 to 65.
Benefits of using F#
The computation kernels are implemented in F# using work flows (also known as computation expressions or monads) and code quotations, a feature-complete and flexible way of using the Alea GPU framework. In our experience the resulting performance is clearly competitive with that of raw CUDA C++ code.
Using F# through Alea GPU permits much higher programmer productivity, both because F#’s concise mathematical notation suits the application area, and because F# has a better compiler-checked type system than C++. For instance, the confusion of device pointers and host pointers that may arise in CUDA C++ is avoided entirely in F#. Hence much less time is spent chasing subtle bugs and mistakes, which is especially important for experimentation and exploration of different implementation strategies. The core Runge-Kutta 4 solver code looks like the following snippet, using code quotations and imperative F# constructs.
let! kernel = <@ fun (input:deviceptr) (output:deviceptr) ... ->
...
while iterDir y do
bj.Invoke (float(y)) (input+inputIndexing.Invoke i boundaryConditionLength) tmp nV
daxpy.Invoke 1.0 v tmp v nV
for s = 0 to steps-1 do
let t = float(y) + (float(s)/float(steps)) * dir;
// k1 = ...
dV.Invoke steps ... v k1
dax.Invoke h2 k1 k1 nV
daxpy.Invoke 0.5 k1 v tmp nV
// k2 = ...
dV.Invoke steps ... tmp k2
dax.Invoke h2 k2 k2 nV
daxpy.Invoke 0.5 k2 v tmp nV
// k3 = ...
dV.Invoke steps ... tmp k3
dax.Invoke h2 k3 k3 nV
daxpy.Invoke 1.0 k3 v tmp nV
// k4 = ...
dV.Invoke steps ... tmp k4
dax.Invoke h2 k4 k4 nV
// v(n+1) = v + k1/6 + k2/3 + k3/3 + k4/6
daxpy.Invoke (1.0/6.0) k4 v tmp nV
daxpy.Invoke (2.0/6.0) k3 tmp tmp nV
daxpy.Invoke (2.0/6.0) k2 tmp tmp nV
daxpy.Invoke (1.0/6.0) k1 tmp v nV
output.[(pos+y+int(dir)-a)]
At the same time, F#’s code quotations, or more precisely the splicing operators, provide a simple and obvious way to inline a function such as GMMale into multiple kernels without source code duplication:
let stocasticMarriageProbabilityODE_technical = <@ fun (x:float) ... (res:deviceptr) ->
let GMMale = %GMMale
...
While similar effects can be achieved using C preprocessor macros, F# code quotations and splice operators do this in a much cleaner way, with better type checking and IDE support. What’s more, F# code quotations allow kernels to be parameterized with both “early” (or kernel compile-time) arguments such as map, and late (or kernel run-time) arguments such as n and isPremium:
let Reserve_GF810_dV_Technical (map:Map<Funcs,Expr>) = <@ fun (n:int) ... (isPremium : int) ->
let GMMale = %%map.[Funcs.GMFemale]
...
Future benefits of using F#
An additional reason for using F# is that in the longer term we want to automatically generate the GPU kernels that solve Thiele’s differential equations. The input to the code generator is a description of the underlying state models (describing life, death, disability and so on) and the functions and tables that express age-dependent mortalities, time-dependent future interest rates, and so on. As a strongly typed functional language with abstract data types, pattern matching, and higher-order functions, the F# language is supremely suited for such code generation processes. The state models and auxiliary functions are described by recursive data structures (so-called abstract syntax), and code generation proceeds by traversing these data structures using recursive functions.
Also, the F# language supports both functional programming, used to express the process of generating code on the host CPU, and imperative programming, used to express the computations that will be performed on the GPU. In other words, high-level functional code generates low-level imperative code, both within the same language, which even supports scripting of the entire generate-compile-load-run cycle:
let compileAndExecute template (inputArray:float[]) ... (b:float[]) =
let irm = Compiler.Compile(template).IRModule
use program = Worker.Default.LoadProgram(irm)
let resultsWithTime = program.Run inputArray ... b
resultsWithTime
The code generation approach will help support a wide range of life insurance and pension products. There are of course alternatives to code generation: First, one might hand-write the differential equations for each product, but this is laborious and error-prone and slows down innovation and implementation, or severely limits the range of insurance products supported. Second, one might take an interpretive approach, by letting the (GPU) code analyze the abstract syntax of the product description, but this involves executing many conditional statements, for which the GPU hardware is ill-suited as it may lead to branch divergence. Hence code generation is the best way to support generality while maintaining the highest performance.
Acknowledgements
This work was done in the context of the Actulus project, a collaboration between Copenhagen University, the company Edlund A/S, and the IT University of Copenhagen, funded in part by the Danish Advanced Technology Foundation contract 017-2010-3. Thanks are due to the many project participants who contributed to AML and in particular due to Christian Gehrs Kuhre and Jonas Kastberg Hinrichsen for their many competent experiments with GPU computations for advanced insurance products. Quantalea graciously provided experimental licenses for Alea GPU and supported us in various GPU related aspects.
Daniel Egloff also contributed to this post. To learn more about Alea GPU and .NET GPU programming, I recommend that you attend Daniel’s tutorial, “Simplified CUDA Development with C#” at GTC 2016 on Monday, April 4 at 10:30. To get a 20% discount on your GTC registration, register using the discount code S7B2XS.