Related Resources
对话式人工智能

基于熵的字级 ASR 置信度估计方法

2023年 1月 13日
By

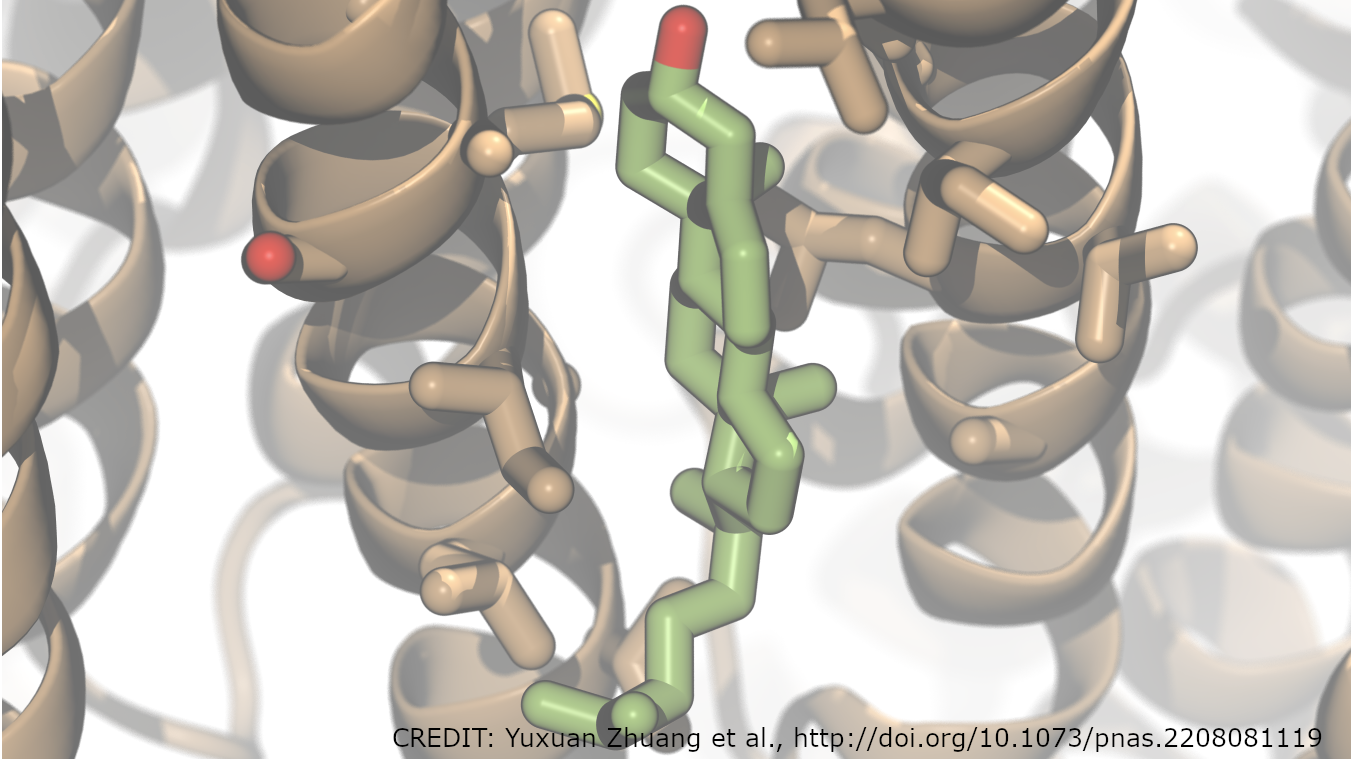
一旦您有了自动语音识别（ ASR ）模型预测，您可能还想知道这些预测正确的可能性。这种正确率或置信度通常作为原始预测概率（快速、简单且可能无用）来衡量。您还可以训练单独的模型来估计预测置信度（准确，但复杂且缓慢）。这篇文章解释了如何使用基于熵的方法实现快速、简单的单词级 ASR 置信度估计。

置信度估计概述

你有没有见过机器学习模型预测，并想知道这种预测有多准确？您可以根据在类似测试用例中测量的准确度进行猜测。例如，假设您知道 ASR 模型以 10% 的单词错误率（ WER ）预测录制语音中的单词。在这种情况下，您可以预期该模型识别的每个单词都有 90% 的准确率。

对于某些应用程序来说，这样的粗略估计可能就足够了，但如果您想确切地知道哪个单词更可能正确，哪个单词不正确呢？这将需要使用超出实际单词的预测信息，例如从模型接收的准确预测概率。

使用原始预测概率作为置信度的度量是判断哪个预测更可能正确、哪个预测不太可能正确以及哪个预测最简单的最快方法。

但原始概率作为置信度估计有用吗？不是真的。例如，图 1 是贪婪搜索识别结果的置信度计算：一帧一帧地计算概率最高的语言单元（“最大概率”或F_{max}(p)），然后汇总成单词级得分。你可以看到的是“过度自信”，当预测概率分布偏向最佳假设时，这是模型的一个特征。

换言之，该模型几乎总是给出一个接近于一个可能预测的概率，而其他任何预测的概率都为零。因此，即使预测不正确，其概率也通常大于 0.9 。过度自信与模型的架构或组件无关：简单的卷积或递归神经网络可以具有与 transformer 或类似 transformer 的模型相同的过度自信程度。

过度自信来自用于训练端到端 ASR 模型的损失函数。当目标预测概率最大化时，简单损失达到最小值，而任何其他预测概率为零。这些损失包括交叉熵、普遍的连接主义时间分类（ CTC ）或递归神经网络传感器（ RNN-T ），或任何其他最大似然族损失函数。

过度自信使预测概率变得不自然。很难设置正确的阈值来区分正确和错误的预测，这使得使用原始概率作为置信度几乎是无用的。

Six log histograms of correctly and incorrectly recognized words against their confidence scores. Aggregation pushes confidence scores of incorrect words toward zero. However, these confidence aggregation functions do little to separate the distribution of correct predictions from incorrect ones: the shapes of correct and incorrect distributions mirror each other.
图 1 。正确和错误识别的单词与其置信分数的堆积对数直方图。子图（ a ）和（ d ）用属于同一单词的帧的预测的平均值获得，（ b ）和（ e ）用最小值获得，以及（ c ）和（ f ）用乘积（\Pi）获得。

使用原始概率作为置信度的另一种选择是创建单独的可训练置信度模型，以基于概率和（可选） ASR 模型嵌入来估计置信度。这种方法可以提供相当准确的置信度，代价是训练每个模型的估计器，将其与主模型一起纳入推理（并不可避免地减慢推理速度），并且缺乏可解释性。

然而，如果你想要最佳的正确性度量，并且对神经网络估计另一个神经网络的系统感到满意，那么试试神经置信度估计器。

基于熵的置信度估计

本节介绍了一种不可训练但有效的置信度估计方法。您将学习如何在贪婪搜索识别模式下为 CTC 和 RNN-T ASR 模型建立快速、简单、鲁棒和可调整的置信度估计方法。

一种简单的基于熵的置信测度

如上所述，将置信度简单地视为原始预测概率是不可行的。最好将此定义扩展到区间[0 , 1]上所有可用知识的函数。将预测概率“按原样”归为这个定义。这种方法使您能够尝试在评估中添加外部知识或以新的方式使用现有信息（概率）。

信心必须忠于其主要目的，即衡量正确性。至少，它必须这样做：为更可能正确的预测分配更高的值。

作为一种置信度度量，熵在理论上是合理的，并且运行良好。在信息论中，熵是不确定性的度量，它基于所有可能结果的概率来计算不确定性值。

这正是具有贪婪解码模式的 ASR 所需要的，其中每个概率向量只有一个预测。只需将熵值分配给预测。然后反转熵值（使其“确定”）并将其归一化（将其映射到[0 , 1]），如下所示。

F_{g}(p) = 1 - \frac{H_{g}(p)}{\max H_g(p)} = 1 + \frac{1}{\ln V } \sum p_v \ln(p_v)

H_g(p)是 Gibbs entropy （当处理自然对数概率时，它比 Shannon entropy 更方便），V是可能预测的数量（ ASR 模型的词汇大小），F_{g}(p)是吉布斯熵置信度。注意，如果模型完全不确定（所有概率都是 1 /V），即使仍然有 1 /V的机会正确猜测预测，置信度也将为零。

这种规范化很方便，因为它不依赖于可能的函数的数量，并且给你一个简单的经验法则：接受接近于 1 的函数，放弃接近于 0 的函数。

基于熵的高级置信测度

上述基于熵的置信度估计在这种形式下非常适用，但仍有改进的空间。虽然理论上正确，但它永远不会显示值​​由于模型的过度自信，在实践中接近于零（当所有概率相等时）。

此外，它不能以这种形式解决不同程度的过度自信。第二个问题很棘手，但第一个问题可以通过不同的标准化来解决。指数运算在这里会有所帮助。当负数被提升为幂时，结果将位于区间[0 , 1]内，并且对于大多数参数接近于零。

使用此属性，可以使用以下公式规范化熵：

F^{e}_{g}(p) = \frac{e^{-H_{g}(p)} - e^{-\max H_{g}(p)}}{1 - e^{-\max H_{g}(p)}} = \frac{V \cdot e^{(\sum p_v \ln(p_v))} - 1}{V - 1}

F^{e}_{g}(p)是指数归一化吉布斯熵置信度。

要使基于熵的信心对过度自信具有真正的鲁棒性，需要一种称为 temperature scaling 的方法。此方法将 log softmax 乘以一个 0 <T< 1 的数字。它通常应用于原始预测概率，以重新校准它们，但并不能显著提高置信度​​T的。具体来说，除非以下不等式成立，否则熵不能通过上述公式归一化。最大熵不会在所有概率相等的点。

\frac{1}{ln(V)} \leq T \leq \frac{1}{ln(\frac{V}{V-1})}

不等式的右侧对于T总是正确的，但左侧施加了限制。例如，如果V= 128 ，则不能低于T= 0.21 。记住这个限制是很乏味的，所以我建议你不要在温度缩放中使用规则熵。

幸运的是，你不必自己将温度代入熵。二十世纪引入了一些参数熵。其中包括统计热力学中的 Tsallis entropy 和信息论中的 Rényi entropy ，这将在下文中讨论。两者都有一个特殊的参数\alpha，称为熵指数，其工作方式类似于温度标度在 0 <\alpha< 1 。他们的指数归一化置信公式如下：

F^{e}_{ts}(p) = \frac{e^{\frac{1}{1 - \alpha} (V^{1 - \alpha} - \sum p_v^{\alpha})} - 1}{e^{\frac{1}{1 - \alpha} (V^{1 - \alpha} - 1)} - 1}

F^{e}_{r}(p) = \frac{V \bigl(\sum p_v^{\alpha}\bigl)^{\frac{1}{\alpha - 1}} - 1}{V - 1}

F^{e}_{ts}(p)和F^{e}_{r}(p)分别是 Tsallis 和 R é nyi 置信度度量。注意， R é nyi 指数归一化是以 2 为基数执行的，以匹配对数并简化公式。这些置信度可能看起来很吓人，但它们并不难实施，而且计算速度几乎与最大概率置信度一样快。

置信预测聚合

到目前为止，本文已经考虑了单个概率向量或单个帧的置信度估计。本节介绍了单词级预测的完整置信度估计方法，引入了预测聚合。

基于熵的置信度可以以与最大概率相同的方式聚合：平均值、最小值和属于同一单词的帧预测的乘积。无论采取何种措施，在聚合 ASR 置信度预测时必须回答两个问题： 1 ）如何将预测聚合到语言单元，而不是将语言单元聚合到单词，以及 2 ）如何处理所谓的 帧（预测 令牌的帧）。和以前一样，第一个问题很简单，第二个问题很棘手。

RNN-T 模型每次发生时只发出一个非 令牌，因此您可以简单地将此预测作为单位级别的置信度，并将其放入单词置信度聚合。 CTC 模型可以在相应单元发音时重复发出相同的非 令牌。我发现对单位和单词使用相同的聚合函数已经足够好了，但总的来说还有实验的空间。

有两种方法可以处理 帧进行置信度聚合：使用它们或丢弃它们。虽然第一个选项看起来很自然，但它迫使您精确地找出如何将它们分配给最近的非 单元。

你可以把它们放在最左边的单位，只放在最靠近的单位，或者其他什么地方，但最好把它们放下。为什么？除了更容易之外，这为基于熵的高级度量提供了（令人惊讶的）更好的结果。这在理论上也更为合理： 预测包含有关在说话时未被识别的单元和单词的信息（所谓的删除）。如果您试图将 置信度分数合并到聚合管道中，您可能会用有关删除单元的信息污染您的置信度。

评估结果和使用提示

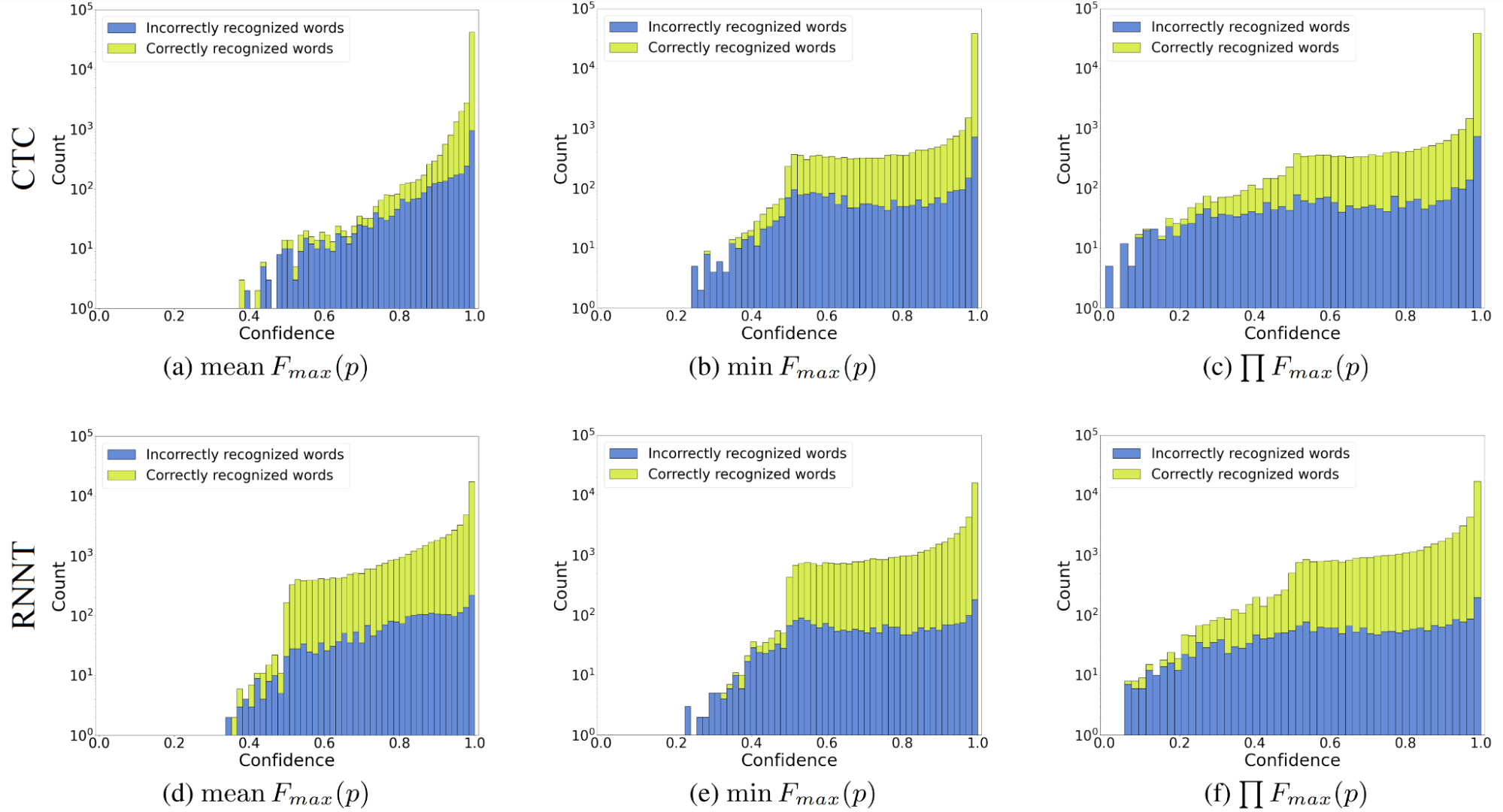
现在，看看所提出的基于熵的置信度估计方法是否优于最大概率置信度。图 2 可能与图 1 相似，具有最大概率置信分布，但您可以看到基于熵的方法转换正确和错误的单词分布，以便更好地分离。（不同的分布形状表示更好的可分离性。）

所有三种方法都涵盖了整个置信谱。尽管产品聚合对于指数归一化吉布斯熵置信度表现最好，但该熵本身并不能很好地处理过度自信。基于 Tsallis 熵的置信度\alpha= 1 / 3 ，在平均值和最小聚合中表现良好。然而，我更喜欢最小值，因为它更集中地减少了对不正确单词的信心。总的来说，指数归一化给出了置信谱的全覆盖，高级熵优于简单熵。

 

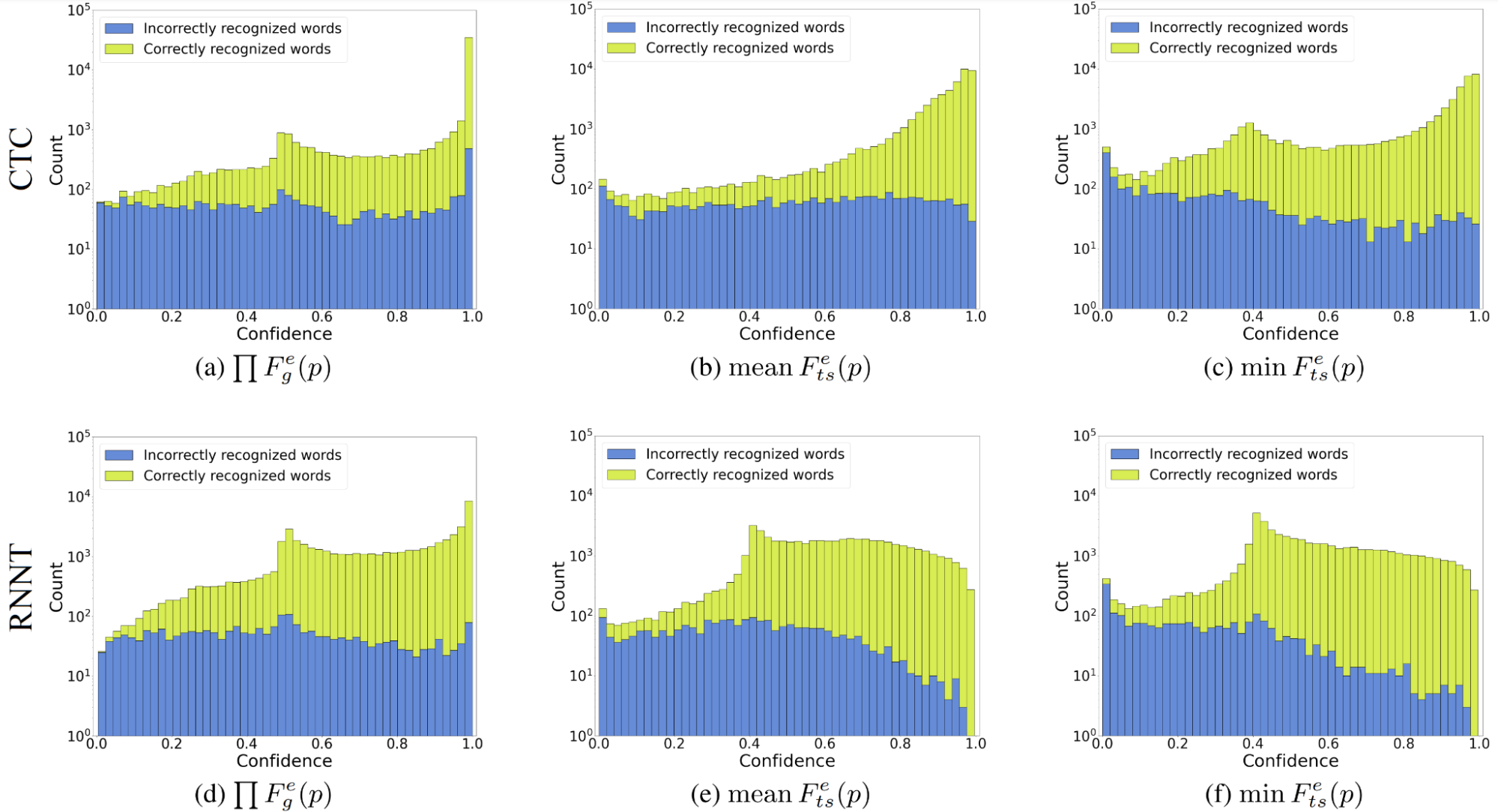
CTC and RNN-T predictions for the exponentially normalized Gibbs entropy-based confidence estimation method with product aggregation are slightly overconfident with the uniform incorrect word distribution and the trend of correct words to confidence score 1. For CTC, the exponentially normalized Tsallis and entropy-based method with mean aggregation pushed correct words towards 1, keeping incorrect words distributed uniformly. For RNN-T, the method pushed incorrect words towards 0, holding the correct ones on a plateau from 0.4 to 1. The exponentially normalized Tsallis entropy-based method with minimum aggregation minimized confidence for incorrect words more intensively than the mean-aggregated method.
图 2 :如图 1 所示，正确和错误识别的单词与其置信度得分的堆积对数直方图，但置信度估计方法不同

比较中的 R é nyi 熵在哪里？基于 Tsallis 和 R é nyi 的方法的性能几乎相同，尽管它们的公式存在明显差异（图 3 ）。对于相同的\alpha和聚集， Tsallis 熵以正确分布的偏移峰值为代价给出了稍微更强的分布分离。我更喜欢基于 Tsallis 的置信度方法，但很有可能 R é nyi 更适合您的特定情况，因此我建议尝试两者。

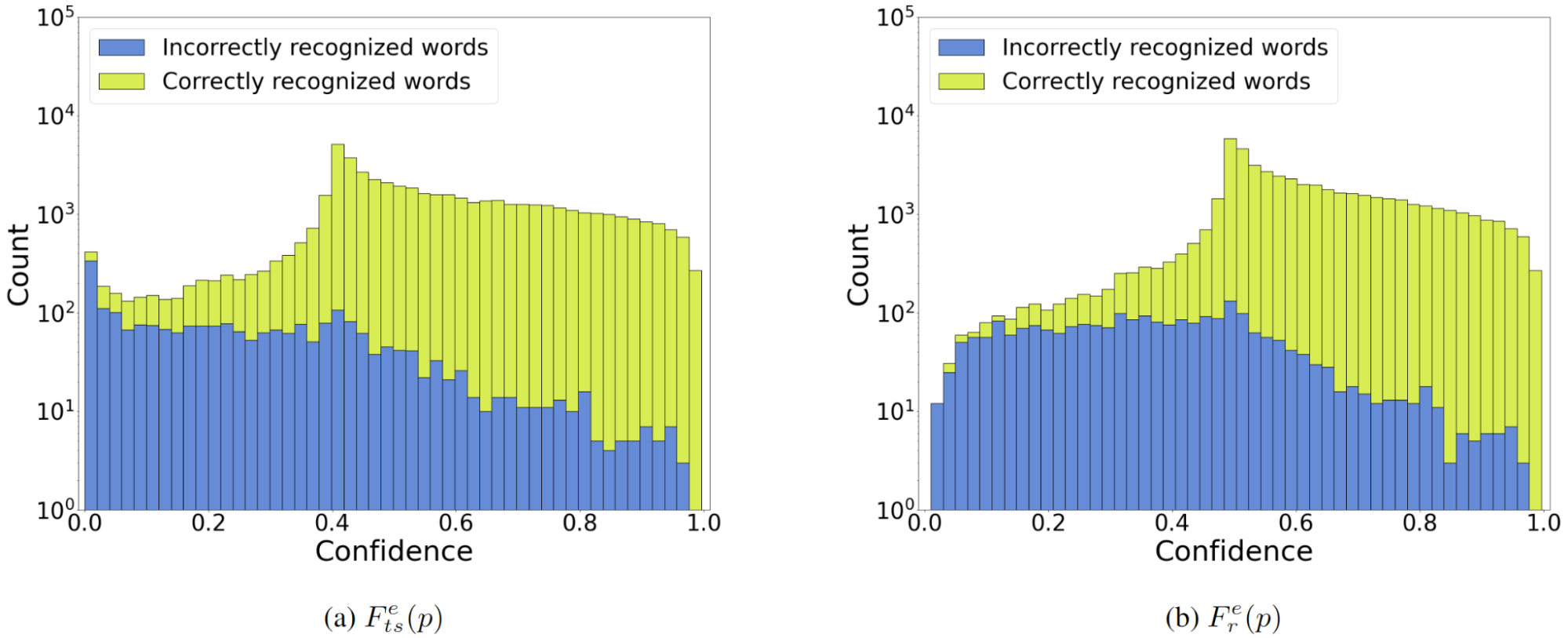
Two similar log-histograms of correctly and incorrectly recognized words against their confidence scores. The left one is for the Tsallis entropy-based method and the right one is for the Rényi. On the left histogram, the incorrect word distribution peaks at confidence 0, a plateau from 0 to 0.4, and a gentle slope from 0.4 to 1. The correct word distribution increases sharply from 0 to a peak at 0.4, after which it plateaus to 1. On the right histogram, both distributions have peaks at 0.5, and all other properties are similar to the left histogram.
图 3 。基于 Tsallis 和 R é nyi 熵的 RNN-T 模型置信度估计方法的比较

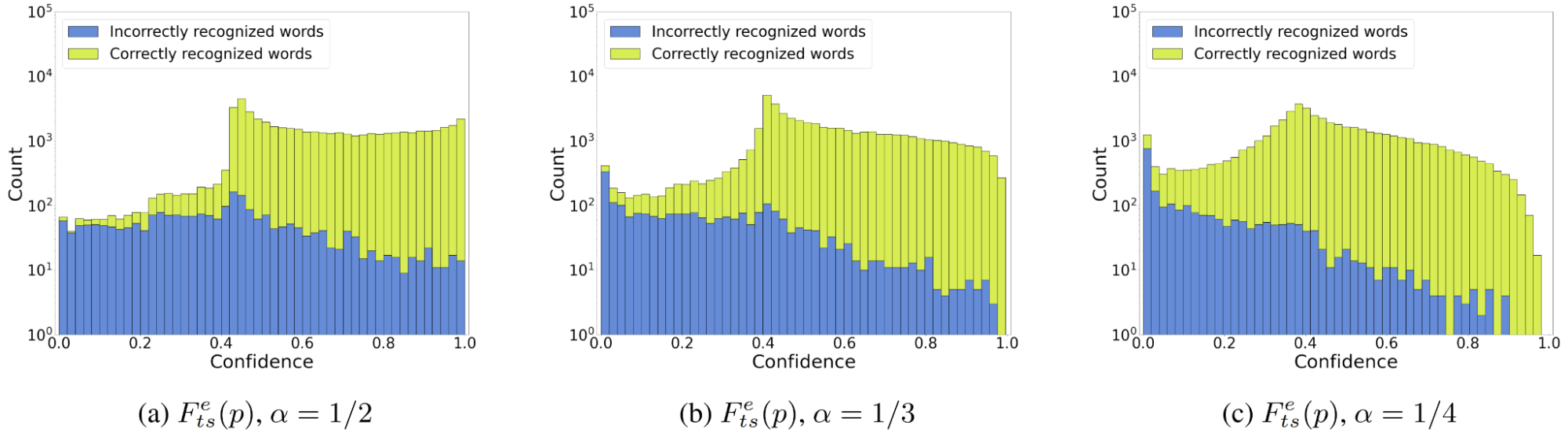
最后一个问题是如何选择\alpha。答案取决于 ASR 模型的过度自信（过度自信越强，\alpha应该越小）以及您想要实现的结果。将\alpha设置得足够小，以获得最佳的分布可分性（图 4 ）。

如果您愿意牺牲分数的自然性（获得正确预测的合理高置信分数）以获得更好的分类能力，则应选择较小的\alpha。

Three similar log-histograms of correctly and incorrectly recognized words against their confidence scores. From left to right, they correspond to alpha values ½, ⅓, and ¼. The left histogram has two peaks near 0.4 and 1 for the correct word distribution and a plateau between them. The incorrect distribution also has a peak near 0.4, a plateau from the left, and a gentle slope from the right. The center and the right histograms are very much alike, with only two differences: the incorrect distribution of the right histogram does not reach 1, while the correct distribution has a flatter slope from 0.4 to 0.
图 4 。不同\alpha之间的比较 具有 RNN-T 模型的基于 Tsallis 熵的方法的值

剩下的是对提出的基于熵的方法的正式评估。首先，基于熵的置信度估计方法在检测错误单词方面比最大概率方法好四倍。第二，所提出的估计器具有噪声鲁棒性，允许您以在常规声学条件下丢失 5% 正确单词的代价过滤掉多达 40% 的模型幻觉（基于纯噪声数据测量）。最后，基于熵的方法给出了 CTC 和 RNN-T 模型的相似度量分数。这意味着您可以使用 RNN-T 模型预测的置信度分数，这在以前是不实际的。

结论

这篇文章提供了三个主要要点：

  1. 使用 Tsallis 和 Rényi 基于熵的置信度代替原始概率作为 ASR 贪婪搜索识别模式的正确性度量。它们速度一样快，而且更好。
  2. 调整测试集上的熵指数\alpha（熵的温度缩放模拟）。或者，您可以只使用 1 / 3 。
  3. 尝试你自己的想法，找到比熵更好的信心度量。

有关拟议方法评估的详细信息，请参见 Aleksandr Laptev 和 Boris Ginsburg 的 Fast Entropy-Based Methods of Word-Level Confidence Estimation for End-To-End Automatic Speech Recognition 。

NVIDIA NeMo 中提供了所有方法以及评估指标。访问 GitHub 上的 NVIDIA/NeMo 开始。

 

Tags

对话式人工智能 | NeMo | Automatic Speech Recognition (ASR) | featured | research | Technical Walkthrough

关于作者

Aleksandr Laptev 是 ITMO 大学的博士生，也是 NVIDIA 的高级研究科学家。他的科学兴趣是自动语音识别、语音合成（ TTS ）和自然语言处理。他撰写开放获取科学文章，为开放源代码软件做出贡献，并参加国际语音识别比赛。他目前的研究领域是可微加权有限状态传感器。