
nvmath-python
nvmath-python (Beta) is an open source library that bridges the gap between Python scientific community and NVIDIA CUDA-X™ math Libraries by reimagining Python’s performance-oriented APIs. It interoperates with and complements existing array libraries such as NumPy, CuPy, and PyTorch by pushing performance limits to new levels through such capabilities as stateful APIs, just-in-time kernel fusion, custom callbacks, and scaling to many GPUs.
Python practitioners, library developers, and GPU kernel writers are finding nvmath-python a powerful tool for getting their scientific, data science, and AI workflows scale with minimum effort.
Install with pipInstall with conda
Other Links:
Key Features
Intuitive Pythonic APIs
nvmath-python reimagines math library APIs to cover sophisticated use cases, which are impossible with NumPy-like APIs without performance compromises.
Host APIs provide both out-of-the-box simplicity and versatility of customization options through optional arguments for accessing all “knobs” of the underlying NVIDIA math libraries. Host APIs are divided into generic and specialized APIs. Generic APIs are intended for a consistent user experience across memory/execution spaces. They may not work with some data types, which are hardware specific and they do not necessarily leverage specific device capabilities. They are great for writing portable code. In contrast, specialized APIs have narrower applications, they may only work on a specific hardware only. They are great for fully leveraging hardware capabilities at the expense of portability.
Device APIs allow embedding nvmath-python library calls in custom kernels, written using Python compilers such as numba-cuda. You no longer need to write GEMM or FFT kernels from scratch.
Host APIs with callbacks allow embedding custom Python code into nvmath-python calls. Internal JIT machinery compiles the custom code and fuses with nvmath-python operation to achieve peak performance.
Stateful (class-form) APIs allow splitting the entire math operation into specification, planning, autotuning, and execution phases. Having an expensive specification, planning, and autotuning done once, allows their cost amortization through multiple subsequent executions.
Integration with the Python logging facility brings visibility into specification, planning, autotuning, and execution machinery details at runtime.
Interoperability With Python Ecosystem
nvmath-python works in conjunction with popular Python packages. This includes GPU-based packages like CuPy, PyTorch, and RAPIDS and CPU-based packages like NumPy, SciPy, and scikit-learn. You can keep using familiar data structures and workflows while benefiting from accelerated math operations through nvmath-python.
nvmath-python is not a replacement for array libraries such as NumPy, CuPy, and PyTorch. It does not implement array APIs for array creation, indexing, and slicing. nvmath-python is intended to be used alongside these array libraries. All these dependencies are optional, and you’re free to choose which array library (or multiple libraries) to work with alongside nvmath-python.
nvmath-python supports CPU and GPU execution and memory spaces. It eases the transition between CPU and GPU implementations as well as allows implementing hybrid CPU-GPU workflows.
In combination with Python compilers, such as numba-cuda, you can implement GPU custom kernels with embedded nvmath-python library calls.
Scalable Performance
nvmath-python pushes performance limits to an edge by delivering performance comparable to the underlying CUDA-X native libraries, such as cuBLAS family, cuFFT family, cuDSS, and cuRAND. With stateful APIs you can amortize the costs of specification, planning, and autotuning phases through multiple executions.
For CPU execution nvmath-python leverages the NVPL library for the best performance on NVIDIA Grace™ CPU platforms. It also supports acceleration of x86 hosts by leveraging the MKL library.
In combination with Python compilers, such as numba-cuda, you can now write highly performant kernels involving GEMM, FFT, and/or RNG operations. Here are just a few examples of impossible made possible with nvmath-python:
nvmath-python allows scaling beyond a single GPU and even beyond a single node without major coding effort. Multi-GPU multi-node (MGMN) APIs allow easy transition from a single GPU implementation to MGMN and seamlessly scale to thousands of GPUs. The library also offers helper utilities for reshaping data (re-partitioning) as needed without major coding.
Supported Operations
Dense Linear Algebra - Generalized Matrix Multiplication
The library offers a GEneralized Matrix Multiplication (GEMM) that performs
𝐃 = 𝐹(ɑ ⋅ 𝐀 ⋅ 𝐁 + β ⋅ 𝐂), where 𝐀, 𝐁, 𝐂 are matrices of compatible dimensions and layouts, ɑ and β are scalars, and 𝐹(𝐗) is a pre-defined function (epilog) which is applied elementwise to matrix 𝐗.
Documentation
Generic Host APIs (coming soon)
Distributed APIs (coming soon)
Tutorials and examples
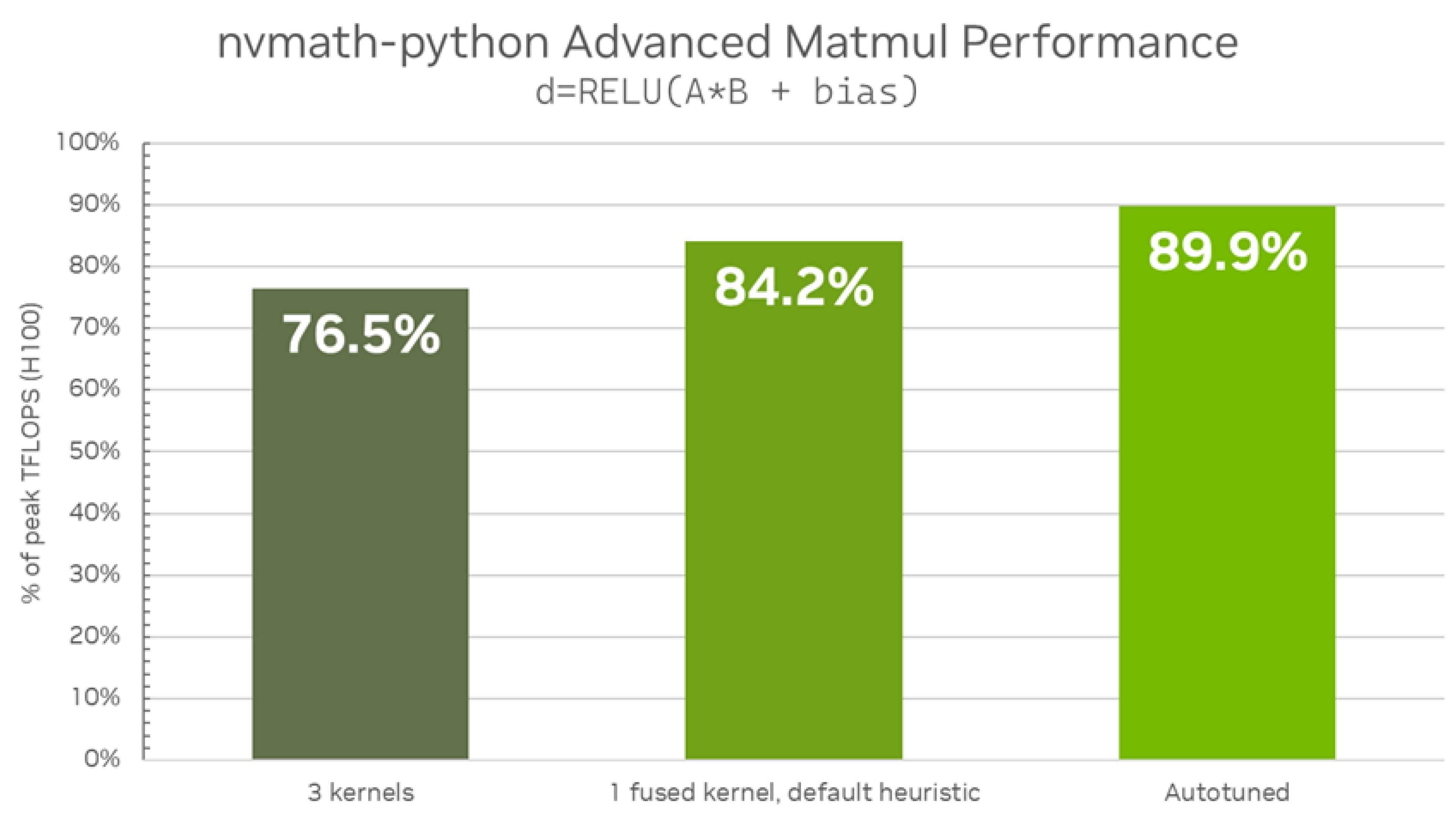
Host APIs provide a specialized API located in nvmath.linalg.advanced submodule backed by cuBLASLt library. This API supports GPU execution space only. The key distinguishing feature of the library is an ability to fuse matrix operations and epilog in a single fused kernel. The library also offers facilities to perform additional autotuning allowing the best fused kernel selection for a specific hardware and a specific problem size. Both stateful and stateless APIs are provided. Generic APIs will be implemented in a future release.
Device APIs are located in the nvmath.device submodule backed by cuBLASDx library. They can be used from within numba-cuda kernels.
Distributed APIs will be implemented in a future release.
Fast Fourier Transforms
The library offers forward and inverse FFTs for complex-to-complex (C2C), complex-to-real (C2R), and real-to-complex (R2C) discrete Fourier transformations.
Documentation
Tutorials and examples
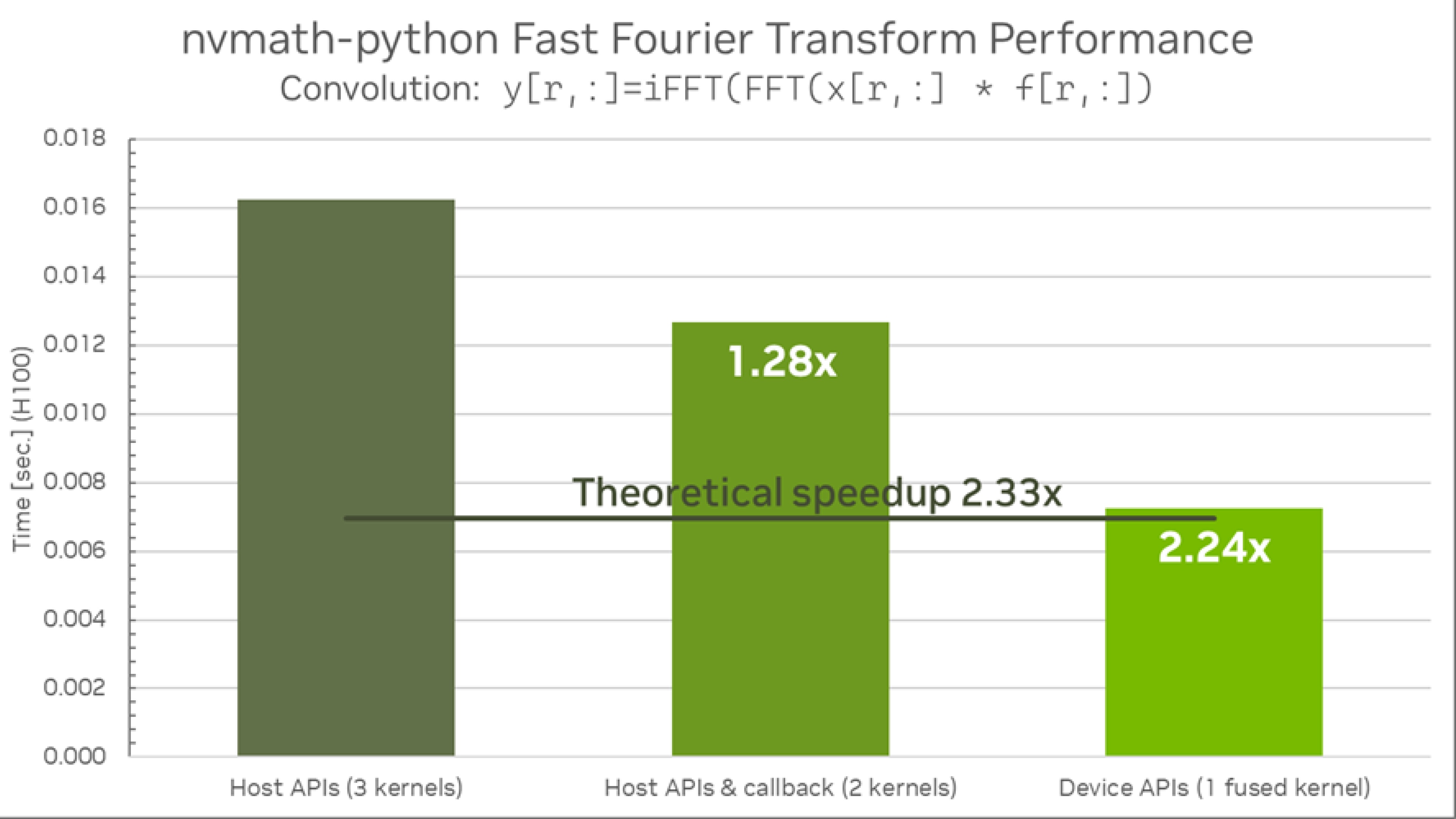
Host APIs are located in the nvmath.fft submodule backed by cuFFT library. The APIs support both CPU and GPU execution spaces. NVIDIA Grace™ CPU platforms are powered by the NVPL library whereas for x86 hosts MKL is offered as a CPU backend. The key distinguishing feature of the library is an ability to fuse an FFT operation and a custom callback written as a Python function into a single fused kernel. The library also offers facilities to perform additional autotuning allowing the best fused kernel selection for a specific hardware and a specific problem size. Both stateful and stateless APIs are provided.
Device APIs are located in the nvmath.device submodule backed by cuFFTDx library. They can be used from within numba-cuda kernels.
Distributed APIs are located in the nvmath.distributed.fft submodule powered by cuFFTMp library, allowing users to solve distributed 2D and 3D FFT exascale problems.
Random Number Generation
The library offers device APIs for performing random number generation from within a GPU kernel written in numba-cuda. It provides a collection of pseudo- and quasi-random number bit generators as well as sampling from popular probability distributions.
Documentation
Tutorials and examples
Device APIs are located in the nvmath.device submodule backed by cuRAND library. They can be used from within numba-cuda kernels for high-performance Monte Carlo simulations on GPU. Please note, the library does not offer corresponding host APIs and rather encourages using random number generation facilities provided by respective array libraries, such as NumPy and CuPy.
Bit RNGs:
MRG32k3a
MTGP Merseinne Twister
XORWOW
Sobol quasi-random number generators
Distribution RNGs:
Uniform distribution
Normal distribution
Log-normal distribution
Poisson distribution
Sparse Linear Algebra - Direct Solver
The library offers specialized APIs to support sparse linear algebra computations. The library currently offers the specialized direct solver API for solving systems of linear equations
𝐀 ⋅ 𝐗 = 𝐁, where 𝐀 is a known left-hand side (LHS) sparse matrix, 𝐁 is a known right-hand side (RHS) vector or a matrix of a compatible shape, and 𝐗 is an unknown solution provided by the solver.
Documentation
Generic Host APIs (in future)
Device APIs (in future)
Distributed APIs (coming soon)
Tutorials and examples

Host APIs provide a specialized API located in nvmath.sparse.advanced submodule backed by cuDSS library. This API supports GPU execution and hybrid GPU-CPU execution space only. The key distinguishing feature of the library is an ability to solve a series of linear systems in batches. The library supports explicit batching, when linear systems are provided as sequences of LHS and/or RHS, and implicit batching, when the sequence is inferred from a higher dimensional tensor. Both stateful and stateless APIs are provided. Generic APIs will be implemented in a future release.
Device APIs will be available in a future release.
Distributed APIs will be implemented in a future release.
Resources
Get started with nvmath-python