As explained in the Batch Normalization paper, training neural networks becomes way easier if its input is Gaussian. This is clear. And if your model inputs are not Gaussian, RAPIDS will just transform it to Gaussian in the blink of an eye.
Gauss rank transformation is a novel standardization technique to transform input data for training deep neural networks. Recently, we used this technique in the Predicting Molecular Properties competition and it easily boosted the accuracy of the message passing neural network model by a significant margin. This blog post will show how simple it is to implement a GPU-accelerated Gauss rank transformation with drop-in replacements of Pandas and NumPy using RAPIDS cuDF and Chainer CuPy to deliver 100x speedup.
Introduction
Input normalization is critical for training neural nets. The idea of Gauss rank transformation was first introduced by Michael Jahrer in his winning solution of Porto Seguro’s Safe Driver Prediction challenge. He trained denoising auto-encoders and experimented with several input normalization methods. In the end, he drew this conclusion:
The best thing I found during the past and works straight out of the box is GaussRank. This works usually much better than standard mean/std scaler or min/max (normalization).
How it works
There are three steps to transform a vector of continuous values under arbitrary distribution to Gaussian distribution based on ranks, as shown in the figure 1.

The CuPy implementation is straightforward and remarkably resembles NumPy operations. In fact, it is as simple as changing the imported functions to move the whole process from CPU to GPU without any other code changes.
Inverse Transformation is used to restore the original values from the Gaussian transformations. This is another great example to show the interoperability of cuDF and CuPy. Just like you can do with NumPy and Pandas, you can weave cuDF and CuPy together in the same workflow while keeping the data entirely on the GPU.
A real-world example
For this example, we will use the CHAMPS molecular properties prediction dataset. The task is to predict scalar coupling constants (the ground truth) between atom pairs in molecules for eight different chemical bond types. What’s challenging is that the distribution of the ground truth differs significantly for each bond type, with varied mean and variance. This makes it difficult for the neural network to converge.
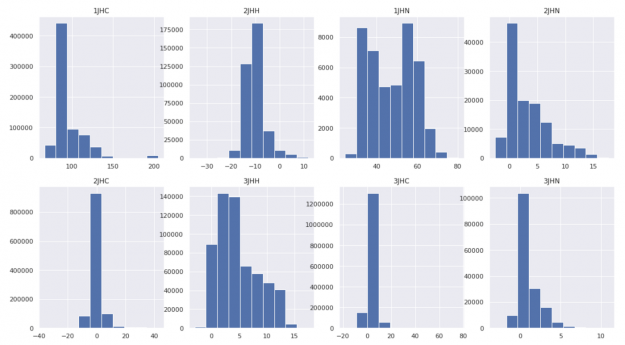
Hence, we applied the Gauss rank transformation to the ground truths of training data to create one unified clean Gaussian distribution for all bond types.
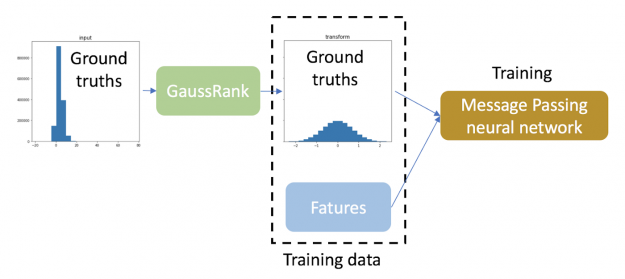
In this regression task, ground truths of training data are transformed using GaussRank.
For inference, we applied the inverse Gauss rank transformation to the predictions of the test data so that they match the original different distributions for each bond type. Since the true distribution of targets of the test data is unknown, the inverse transformation of the predictions of the test data is calculated based on the distribution of target variables in training data. It should be noted that such an inverse transformation is only needed for target variables.
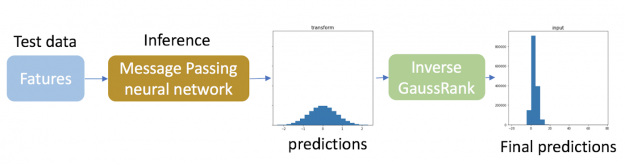
By applying this single trick, the Log of the Mean Absolute Error (LMAE) of our message passing neural network is improved by 18%!
Keep in mind that GaussRank does have some limitations:
- It works only for continuous variables, and
- if the input is already close to Gaussian, or very asymmetrical, performance might not be improved or even become worse.
The interplay between gauss rank transformation and different kinds of neural networks is an active research topic.
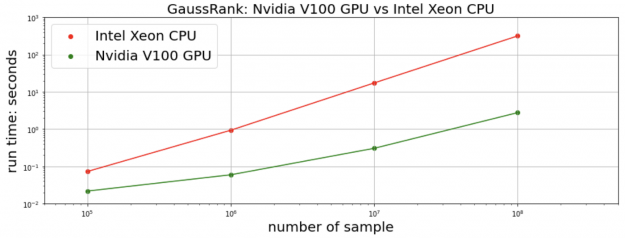
Speedup
We measure the total time of transformation and the inverse transformation. For the proceeding CHAMPS dataset, the cuDF+CuPy implementation on a single NVIDIA V100 GPU achieves 25x speedup over the Pandas+NumPy implementation on an Intel Xeon CPU. We generate synthetic random data for a more comprehensive comparison. For 10M data points and more, our RAPIDS implementation is more than 100x faster.
Conclusion
RAPIDS has come a long way to deliver stunning performance with little or no code changes. This blog post showcases how easy it is to use RAPIDS cuDF and CuPy as drop-in replacements to Pandas and NumPy to realize the performance improvements on GPUs. As shown in the full notebook, by adding just two lines of code, the Gauss rank transformation detects the input tensor is on GPU and automatically switches to cuDF+CuPy from Pandas+NumPy. It can’t be much easier than that.