
My previous CUDA Fortran post covered the mechanics of using shared memory, including static and dynamic allocation. In this post I will show some of the performance gains achievable using shared memory. Specifically, I will optimize a matrix transpose to show how to use shared memory to reorder strided global memory accesses into coalesced accesses.
Matrix Transpose
The code we wish to optimize is a transpose of a matrix of single precision values that operates out-of-place, i.e. the input and output are separate arrays in memory. For simplicity of presentation, we’ll consider only square matrices whose dimensions are integral multiples of 32 on a side. The entire code is available on Github. It consists several kernels as well as host code to perform typical tasks such as allocation and data transfers between host and device, launches and timings of several kernels as well as validation of their results, and deallocation of host and device memory. In this post I’ll only include the kernel code; you can view the rest or try it out on Github.
In addition to performing several different matrix transposes, we run simple matrix copy kernels because copy performance indicates the performance that we would like the matrix transpose to achieve. For both matrix copy and transpose, the relevant performance metric is effective bandwidth, calculated in GB/s by dividing twice the size in GB of the matrix (once for loading the matrix and once for storing) by time in seconds of execution.
All kernels in this study launch blocks of 32×8 threads (TILE_DIM=32, BLOCK_ROWS=8 in the code), and each thread block transposes (or copies) a tile of size 32×32. Using a thread block with fewer threads than elements in a tile is advantageous for the matrix transpose because each thread transposes four matrix elements, so much of the index calculation cost is amortized over these elements.
The kernels in this example map threads to matrix elements using a Cartesian (x,y) mapping rather than a row/column mapping to simplify the meaning of the components of the automatic variables in CUDA Fortran: threadIdx%x is horizontal and threadIdx%y is vertical. This mapping is up to the programmer; the important thing to remember is that to ensure memory coalescing we want to map the quickest varying component to contiguous elements in memory. In Fortran contiguous addresses correspond to the first index of a multidimensional array, and threadIdx%x and blockIdx%x vary quickest within blocks and grids, respectively.
Simple Matrix Copy
Let’s start by looking at the matrix copy kernel.
attributes(global) subroutine copy(odata, idata) implicit none real, intent(out) :: odata(nx,ny) real, intent(in) :: idata(nx,ny) integer :: x, y, j x = (blockIdx%x-1) * TILE_DIM + threadIdx%x y = (blockIdx%y-1) * TILE_DIM + threadIdx%y do j = 0, TILE_DIM-1, BLOCK_ROWS odata(x,y+j) = idata(x,y+j) end do end subroutine copy
Each thread copies four elements of the matrix in a loop at the end of this routine because the number of threads in a block is smaller by a factor of four (TILE_DIM/BLOCK_ROWS) than the number of elements in a tile. Note also that TILE_DIM must be used in the calculation of the matrix index y rather than BLOCK_ROWS or blockDim%y. The loop iterates over the second dimension and not the first so that contiguous threads load and store contiguous data, and all reads from idata and writes to odata are coalesced.
Naive Matrix Transpose
Our first transpose kernel looks very similar to the copy kernel. The only difference is that the indices for odata are swapped.
attributes(global) subroutine transposeNaive(odata, idata) implicit none real, intent(out) :: odata(ny,nx) real, intent(in) :: idata(nx,ny) integer :: x, y, j x = (blockIdx%x-1) * TILE_DIM + threadIdx%x y = (blockIdx%y-1) * TILE_DIM + threadIdx%y do j = 0, TILE_DIM-1, BLOCK_ROWS odata(y+j,x) = idata(x,y+j) end do end subroutine transposeNaive
In transposeNaive the reads from idata are coalesced as in the copy kernel, but for our 1024×1024 test matrix the writes to odata have a stride of 1024 elements or 4096 bytes between contiguous threads. This puts us well into the asymptote of the strided memory access plot from our global memory coalescing post, and we expect the performance of this kernel to suffer accordingly. The results of the copy and transposeNaive kernels bear this out.
| Effective Bandwidth (GB/s, ECC enabled) | ||
| Routine | Tesla M2050 | Tesla K20c |
| copy | 105.6 | 136.2 |
| transposeNaive | 18.8 | 55.2 |
The transposeNaive kernel achieves only a fraction of the effective bandwidth of the copy kernel. Because this kernel does very little other than copying, we would like to get closer to copy throughput. Let’s look at how we can do that.
Coalesced Transpose Via Shared Memory
The remedy for the poor transpose performance is to use shared memory to avoid the large strides through global memory. The following figure depicts how shared memory is used in the transpose.
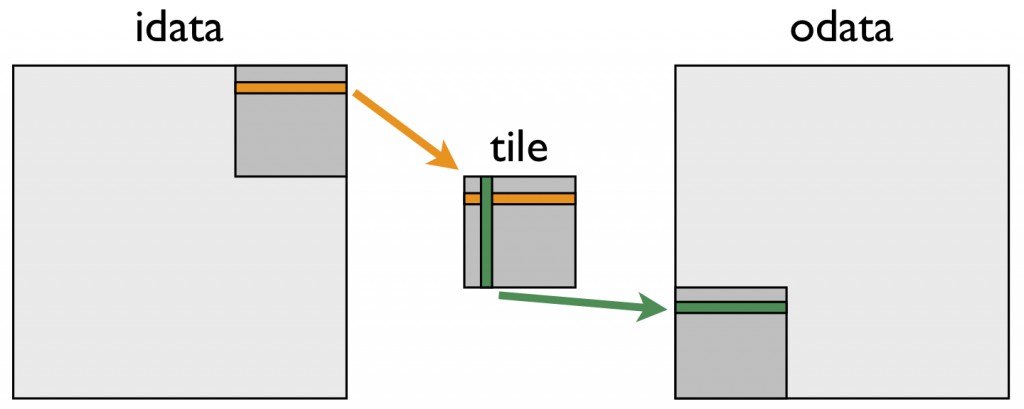
The following kernel performs this “tiled” transpose.
attributes(global) subroutine transposeCoalesced(odata, idata)
implicit none
real, intent(out) :: odata(ny,nx)
real, intent(in) :: idata(nx,ny)
real, shared :: tile(TILE_DIM, TILE_DIM)
integer :: x, y, j
x = (blockIdx%x-1) * TILE_DIM + threadIdx%x
y = (blockIdx%y-1) * TILE_DIM + threadIdx%y
do j = 0, TILE_DIM-1, BLOCK_ROWS
tile(threadIdx%x, threadIdx%y+j) = idata(x,y+j)
end do
call syncthreads()
x = (blockIdx%y-1) * TILE_DIM + threadIdx%x
y = (blockIdx%x-1) * TILE_DIM + threadIdx%y
do j = 0, TILE_DIM-1, BLOCK_ROWS
odata(x,y+j) = tile(threadIdx%y+j, threadIdx%x)
end do
end subroutine transposeCoalesced
In the first do loop, a warp of threads reads contiguous data from idata into rows of the shared memory tile. After recalculating the array indices, a column of the shared memory tile is written to contiguous addresses in odata. Because threads write different data to odata than they read from idata, we must use a block-wise barrier synchronization syncthreads(). This approach gives us a nice speed up, as shown in this updated effective bandwidth table.
| Effective Bandwidth (GB/s, ECC enabled) | ||
| Routine | Tesla M2050 | Tesla K20c |
| copy | 95.8 | 136.2 |
| transposeNaive | 18.0 | 55.2 |
| transposeCoalesced | 51.6 | 93.0 |
The transposeCoalesced results are an improvement over the transposeNaive case, but they are still far from the performance of the copy kernel. One possibility for the performance gap is the overhead associated with using shared memory and the required synchronization barrier syncthreads(). We can easily test this using the following copy kernel that uses shared memory.
attributes(global) subroutine copySharedMem(odata, idata)
implicit none
real, intent(out) :: odata(nx,ny)
real, intent(in) :: idata(nx,ny)
real, shared :: tile(TILE_DIM, TILE_DIM)
integer :: x, y, j
x = (blockIdx%x-1) * TILE_DIM + threadIdx%x
y = (blockIdx%y-1) * TILE_DIM + threadIdx%y
do j = 0, TILE_DIM-1, BLOCK_ROWS
tile(threadIdx%x, threadIdx%y+j) = idata(x,y+j)
end do
call syncthreads()
do j = 0, TILE_DIM-1, BLOCK_ROWS
odata(x,y+j) = tile(threadIdx%x, threadIdx%y+j)
end do
end subroutine copySharedMem
Note that the synchthreads() call is technically not needed in this case, because the operations for an element are performed by the same thread, but we include it here to mimic the transpose behavior. The second line of the table below shows that the problem is not the use of shared memory or the barrier synchronization.
| Effective Bandwidth (GB/s, ECC enabled) | ||
| Routine | Tesla M2050 | Tesla K20c |
| copy | 105.6 | 136.2 |
| copySharedMem | 104.6 | 152.8 |
| transposeNaive | 18.8 | 55.2 |
| transposeCoalesced | 51.6 | 93.0 |
Shared Memory Bank Conflicts
For a shared memory tile of 32 × 32 elements, all elements in a column of data map to the same shared memory bank, resulting in a worst-case scenario for memory bank conflicts: reading a column of data results in a 32-way bank conflict. Luckily, the solution for this is simply to pad the first index in the declaration of the shared memory tile.
real, shared :: tile(TILE_DIM+1, TILE_DIM)
Removing the bank conflicts in this way brings us within 93% of our fastest copy throughput.
| Effective Bandwidth (GB/s, ECC enabled) | ||
| Routine | Tesla M2050 | Tesla K20c |
| copy | 105.6 | 136.2 |
| copySharedMem | 104.6 | 152.8 |
| transposeNaive | 18.8 | 55.2 |
| transposeCoalesced | 51.6 | 93.0 |
| transposeNoBankConflicts | 99.3 | 142.9 |
Summary
In this post we presented three kernels that represent various optimizations for a matrix transpose. The kernels show how to use shared memory to coalesce global memory access and how to pad arrays to avoid shared memory bank conflicts. Looking at the relative gains of our kernels, coalescing global memory accesses is by far the most critical aspect of achieving good performance, which is true of many applications. Because global memory coalescing is so important, we revisit it again in the next post when we look at a finite difference computation on a 3D mesh.





