STAC Research develops financial benchmarks in partnership with leading banks and software or hardware vendors. The STAC-A2 suite of benchmarks aims to represent the standard risk analysis workload that banks and insurance companies use to measure exposure on the financial markets. Earlier this year we published a Parallel Forall post on Monte Carlo simulation for the pricing of American options in STAC-A2.
Record Performance with Tesla K80
Recently, STAC Research published astonishing performance results for the STAC-A2 benchmarks on an NVIDIA Tesla K80. In short, a single Tesla K80 driven by two CPU cores outperforms all previously audited systems in terms of pure performance and power efficiency.
For more on these results, read “Bank on It: Tesla Platform Shatters Record on Risk-Management Benchmark” on the NVIDIA Blog.
 We obtained these new results after several optimizations of our previously audited code. First of all, a large fraction of the computations are now avoided due to a better factorization of the underlying mathematical process. Secondly, we tuned some of the kernel parameters to take advantage of the larger register file of the Tesla K80. Finally, we were able to significantly reduce the latency in one of the main loops of the benchmark. Let’s take a look at these optimizations.
We obtained these new results after several optimizations of our previously audited code. First of all, a large fraction of the computations are now avoided due to a better factorization of the underlying mathematical process. Secondly, we tuned some of the kernel parameters to take advantage of the larger register file of the Tesla K80. Finally, we were able to significantly reduce the latency in one of the main loops of the benchmark. Let’s take a look at these optimizations.
The Longstaff-Schwartz Loop
STAC-A2 uses the Longstaff-Schwartz algorithm to price an American option. Without going into cumbersome details, a single loop which iterates over the time steps contains the main bulk of computations. At each time step, the method determines whether or not to exercise an option. For more details, check out my previous post. In our original implementation, we were using three CUDA kernels for each iteration. Figure 1 shows a timeline of a single iteration captured with the NVIDIA Visual Profiler.
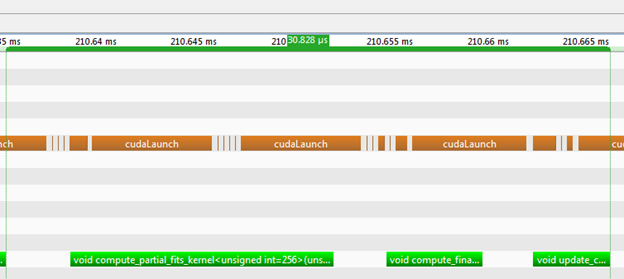
A single iteration of the previous STAC-A2 implementation took about 30.8 μs to run on a Tesla K20 accelerator. The kernels ran for 13.4 μs, 4.9 μs and 3.9 μs, respectively, for a total of 22.2 μs. In other words, within a single iteration, launch latency consumed 8.6 μs, representing almost 28% of the iteration time. The STAC-A2 Greek benchmark runs this loop 93 times for a total of 23,343 iterations. Thus, launch latency represented nearly 200 ms of a run taking about 1.3 seconds on a Tesla K20.
Reducing the Number of Kernels
In order to reduce the impact of launch latency, we decided to merge the three kernels into two. In our original implementation, the first two kernels computed three sums. A standard parallel sum implementation on a GPU uses a two-stage approach. In the first stage, each block of threads computes a partial sum and stores the result into global memory. In the second stage, a single block of threads combines the partial sums. As the following code sample shows, our implementation uses the CUB library. CUB provides flexible, easy-to-use and extremely efficient CUDA implementations of key parallel primitives such as reduction, scan and sort. CUB is like a Swiss Army knife for the CUDA developer and I use it every time I need to do parallel operations.
template< int BLOCK_DIM >
__global__
void sum_kernel(int n, const double *in, double *out)
{
typedef cub::BlockReduce<double, BLOCK_DIM> BlockReduce;
// Shared memory to compute the sum of the block.
__shared__ typename BlockReduce::TempStorage smem_storage;
// Each thread computes its own partial sum.
double sum = 0.0;
int i = blockIdx.x*blockDim.x + threadIdx.x;
for( ; i < n; i += blockDim.x*gridDim.x )
sum += in[i];
// Do a block-level sum.
sum = BlockReduce(smem_storage).Sums(sum);
// The first thread stores the results for the block in global memory
if( threadIdx.x == 0 )
out[blockIdx.x] = sum;
}
const int BLOCK_DIM = 256;
const int m = min(BLOCK_DIM, (n + BLOCK_DIM-1)/BLOCK_DIM);
sum_kernel<block_dim><<<m, BLOCK_DIM>>>(n, d_in, d_out);
sum_kernel<block_dim><<<1, BLOCK_DIM>>>(m, d_out, d_out);
Because we wanted to reduce the impact of launch latency, we decided to change our approach and implement the sum in a different way. Specifically, we decided to remove the second step of the algorithm.
With this objective in mind, we had two choices: use an “atomic” operation to store the result of each block in a single array, or “move” the second step to the beginning of the third kernel. We implemented both strategies. An iteration of the atomic-based implementation ran in 50.4 μs whereas the latter approach gave an iteration time of 25.9 μs (compared to 30.8 μs in the previous implementation). The low performance of the atomic-based implementation was due to the lack of hardware atomic instructions for FP64 values.
Batching Kernels
To further reduce the impact of launch latency, we decided to regroup the computations made by several kernels. The STAC-A2 benchmark runs the Longstaff-Schwartz algorithm for several different scenarios. In our first implementation, we called our Longstaff-Schwartz implementation one scenario at a time. In our latest version of the code, we group several scenarios into a single call to the algorithm. This modification was straightforward to implement within our CUDA kernels by simply adding a dimension to our CUDA grid (2 rather than 1) to launch many more blocks of threads. The main loop, described earlier, executes less frequently and launches each kernel fewer times. Overall this helps reduce the total launch latency.
A positive side effect of the batching is better utilization of the hardware by the kernels in the main loop. Indeed, a single iteration of the loop can execute 10 scenarios in 107 μs on a Tesla K20, which is about 2.4 times faster than computing the 10 scenarios sequentially. The improvement is mostly due to launching larger grids that expose more warp-level parallelism.
As Figure 2 shows, in the case of only 1 scenario per kernel launch, there are on average 9.35 active warps per cycle on each multiprocessor (SM). That number grows to 28.71 when we are able to batch 10 scenarios into a single kernel launch. The immediate impact is that the number of eligible warps per active cycle—that is the number of warps that are ready to issue instructions at each cycle—increases from 1.08 to 3.35.
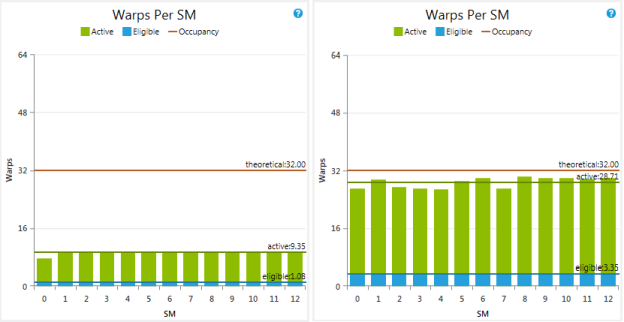
An interesting remark is that, in our tests, the best performance is achieved with blocks of 64 threads even if it limits the theoretical occupancy to 50% (as shown in Figure 2).
Default Stream
Finally, to further improve performance we execute the kernels in the main loop in the default stream. Our previous implementation,executes all operations asynchronously in a user stream, including memory copies (cudaMemcpyAsync), memory sets (cudaMemsetAsync) and kernel launches. However, we decided to launch the kernels in the main loop in the default stream (stream 0), because it has a slightly smaller overhead in CUDA and when the kernels are extremely impacted by the launch latency, it can make a difference. In our case, when we run the main loop in a user stream, the baseline solution takes 702ms whereas it takes 697ms with the default stream (results measured on a Tesla K20c @ 2600, 758MHz, with ECC on).
Conclusion
In our initial CUDA C++ implementation of the STAC-A2 benchmark, launch latency and small grid sizes limited the performance. We were able to detect those limitations using Nsight Visual Studio Edition and the NVIDIA Visual Profiler; both included with the NVIDIA CUDA Toolkit. With limited but targeted modifications of our code we increased the performance significantly to demonstrate that the Tesla K80 accelerator is the fastest and most power-efficient solution for option pricing.
To learn more about GPU code optimization, please join us next March at GTC 2015.