这篇文章最初发表在开发者专区。
深度精度是每一个图形程序员迟早都要面对的难题。关于这个主题已经写了很多文章和论文,在不同的游戏、引擎和设备中可以找到各种不同的深度缓冲格式和设置。
由于它与透视投影交互的方式, GPU 硬件深度映射有点晦涩难懂,研究这些方程可能不会让事情立即变得显而易见。为了获得它如何工作的直觉,画一些图片是很有帮助的。
这篇文章有三个主要部分。在第一部分中,我试图为非线性深度映射提供一些动机。其次,我提供了一些图表来帮助理解非线性深度映射在不同情况下是如何工作的,直观且直观。第三部分是 Paul Upchurch 和 Mathieu Desbrun ( 2012 )关于浮点舍入误差对深度精度影响的提高透视渲染的精度主要结果的讨论和再现。
为什么是 1 / z
GPU 硬件深度缓冲区通常不会存储对象在相机前面的距离的线性表示,这与您第一次遇到这种情况时天真的期望相反。相反,深度缓冲区存储的值与世界空间深度的倒数成比例。我想简要介绍一下这次大会。
在本文中,我使用d表示深度缓冲区中存储的值(在[0 , 1]中),并使用z表示世界空间深度,即沿视图轴的距离,以世界单位(如米)表示。一般而言,它们之间的关系如下:
在此公式中,a和b是与近平面和远平面设置相关的常数。换言之,d始终是.
从表面上看,您可以想象将d作为您喜欢的z的任何函数。那么,为什么会有这种特殊的选择呢?有两个主要原因。
First,自然适合透视投影的框架。这是保证保持直线的最普通的变换类,这使得硬件光栅化变得很方便,因为三角形的直边在屏幕空间中保持笔直。可以生成的线性重映射
通过利用硬件已经执行的透视图划分:
当然,这种方法的真正威力在于投影矩阵可以与其他矩阵相乘,从而允许您将多个变换阶段组合在一个矩阵中。
第二个原因是在屏幕空间中是线性的,如埃米尔·佩尔松所述。因此,在栅格化的同时,在三角形上插值d是很容易的,而像分层 Z 缓冲区、早期 Z 消隐和深度缓冲区压缩这样的事情都要容易得多。
绘制深度图
方程是硬的;这里有一些照片!
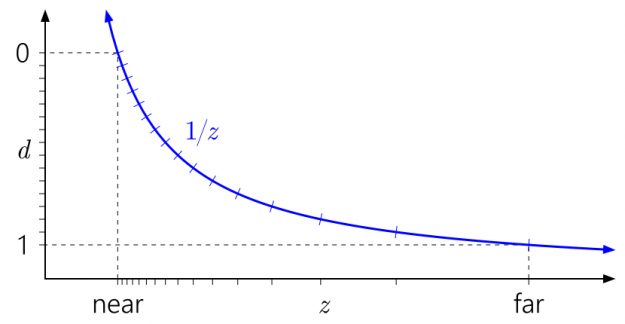
阅读这些图表的方法是从左到右,然后从下到下。从d开始,绘制在左轴上。因为d可以是,您可以将 0 和 1 放置在此轴上任意位置。勾号表示不同的深度缓冲区值。为了便于说明,我正在模拟一个 4 位标准化整数深度缓冲区,因此有 16 个等距记号。
水平追踪刻度线,直到它们击中目标的位置曲线,然后向下至底部轴。这就是世界空间深度范围中不同值的位置。
图 1 显示了 D3D 和类似 API 中使用的“标准”深度映射。您可以立即看到曲线会导致靠近近平面的值聚集在一起,而靠近远平面的值分布得非常分散。
也很容易看出为什么近平面对深度精度有如此深远的影响。拉近近飞机将使d射程向上飞向飞机的渐近线曲线,导致更不平衡的值分布:
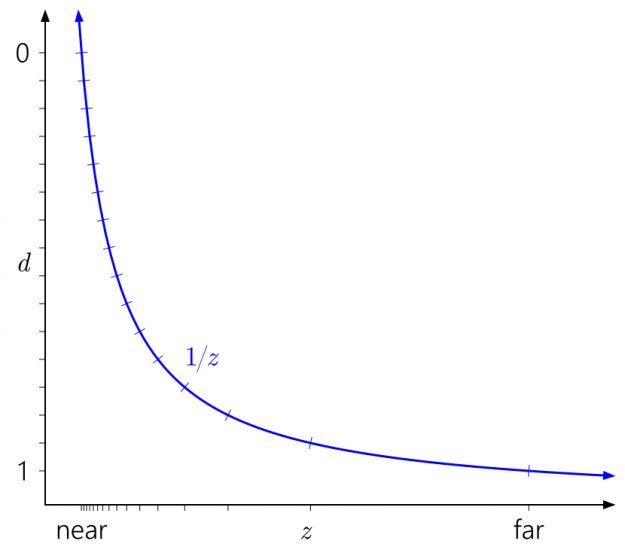
类似地,在这种情况下,很容易看出为什么将远平面一直推到无穷远没有那么大的效果。这只是意味着将d范围稍微向下扩展到:
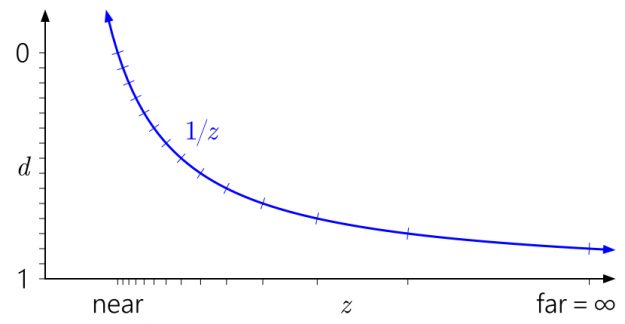
浮点深度呢?下图添加了与具有三个指数位和三个尾数位的模拟浮点格式相对应的记号:
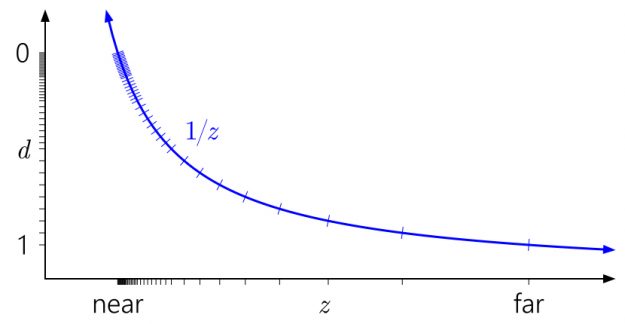
[0 , 1]中现在有 40 个不同的值——比以前的 16 个值多了一点,但它们中的大多数都无用地聚集在不需要更高精度的近平面上。
现在广为人知的一个技巧是反转深度范围,将近平面映射到d=1,将远平面映射到d=0:
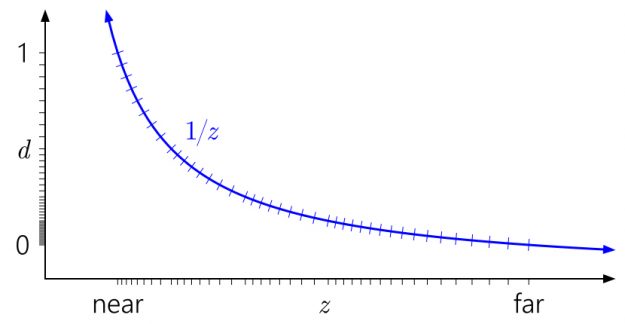
好多了!现在,浮点的准对数分布在某种程度上抵消了非线性,使您在近平面的精度与整数深度缓冲区相似,并大大提高了其他地方的精度。当你向远处移动时,精度只会慢慢降低。
反向 -Z 技巧可能已经被独立地重新发明了好几次,但至少可以追溯到 Eugene Lapidous 和 Guofang Jiao (不幸的是,没有可用的开放访问链接)撰写的 SIGGRAPH ‘ 99 论文低成本图形硬件的最佳深度缓冲。最近,马特·佩蒂尼奥。和布拉诺·凯门以及埃米尔·佩尔松的创造广阔的游戏世界 SIGGRAPH 2012 年讲座在帖子中重新推广了这一概念。
之前的所有图表均假定[0 , 1]为投影后深度范围,这是 D3D 约定。那 OpenGL 呢?
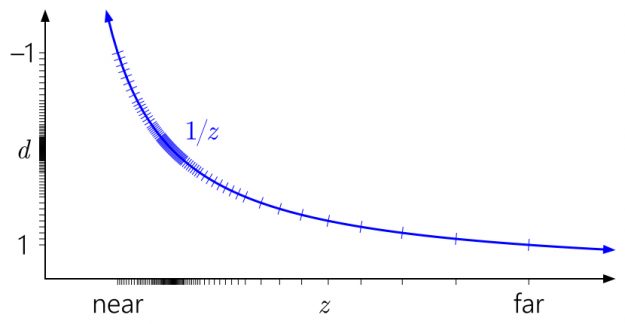
默认情况下, OpenGL 假定投影后深度范围为[-1 , 1]。这对整数格式不起作用,但是用浮点,所有的精度都在中间被无用地卡住。(该值被映射到[0 , 1]以便稍后存储在深度缓冲区中,但这并没有帮助,因为到[-1 , 1]的初始映射已经破坏了该范围最远一半的所有精度。)根据对称性,反转 -Z 技巧在这里没有任何作用。
幸运的是,在桌面 OpenGL 中,您可以通过广泛支持的ARB_clip_control扩展(现在也是 OpenGL 4 . 5 中的核心glClipControl)来解决这个问题。不幸的是,在德国,你运气不好。
舍入误差的影响
The映射和浮点与整数深度缓冲区的选择是精度故事的重要部分,但不是全部。即使您有足够的深度精度来表示要渲染的场景,也很容易最终得到由顶点变换过程的算术错误控制的精度。
如前所述,厄普丘奇和德斯布伦对此进行了研究,并提出了两项主要建议,以尽量减少舍入误差:
- 使用一个无限远的平面。
- 将投影矩阵与其他矩阵分开,并在顶点着色器中的单独操作中应用它,而不是将其组合到视图矩阵中。
Upchurch 和 Desbrun 通过分析技术提出了这些建议,其基础是将舍入误差视为每次算术运算中引入的小随机扰动,并通过转换过程将其跟踪到一阶。我决定使用直接模拟来检查结果。
这是我的源代码 – Python 3 . 4 和 NumPy 。它的工作原理是生成一系列随机点,按深度排序,在近平面和远平面之间线性或对数间隔。然后,它使用 32 位浮点精度将点通过视图和投影矩阵以及透视分割,并可选地将最终结果量化为 24 位整数。
最后,它遍历序列并计算两个相邻点(最初具有不同深度)由于映射到相同深度值而变得不可区分或实际交换顺序的次数。换句话说,它测量深度比较错误发生的速率,这与不同场景下的 Z- 战斗等问题相对应。
以下是近距离= 0 . 1 ,远距离= 10K ,线性间隔深度为 10K 时获得的结果。(我也尝试了对数深度间距和其他近/远比率,虽然详细数字各不相同,但结果的总体趋势是相同的。)
在表中,“不可区分”表示不可区分(两个相邻深度映射到相同的最终深度缓冲区值),“交换”表示两个相邻深度交换顺序。
| Precomposed view Projection matrix |
Separate view and projection matrices |
||||
| float32 | int24 | float32 | int24 | ||
| Unaltered Z values (control test) |
0% indist 0% swap |
0% indist 0% swap |
0% indist 0% swap |
0% indist 0% swap |
|
| Standard projection | 45% indist 18% swap |
45% indist 18% swap |
77% indist 0% swap |
77% indist 0% swap |
|
| Infinite far plane | 45% indist 18% swap |
45% indist 18% swap |
76% indist 0% swap |
76% indist 0% swap |
|
| Reversed Z | 0% indist 0% swap |
76% indist 0% swap |
0% indist 0% swap |
76% indist 0% swap |
|
| Infinite + reversed-Z | 0% indist 0% swap |
76% indist 0% swap |
0% indist 0% swap |
76% indist 0% swap |
|
| GL-style standard | 56% indist 12% swap |
56% indist 12% swap |
77% indist 0% swap |
77% indist 0% swap |
|
| GL-style infinite | 59% indist 10% swap |
59% indist 10% swap |
77% indist 0% swap |
77% indist 0% swap |
很抱歉没有绘制这些,但是有太多的维度,使其易于绘制!不管怎样,看看这些数字,一些普遍的结果是清楚的。
- 在大多数设置中,浮点深度缓冲区和整数深度缓冲区之间没有区别。算术误差淹没了量化误差。这在一定程度上是因为 float32 和 int24 在[0 . 5 , 1]中具有几乎相同大小的 ulp (因为 float32 具有 23 位尾数),因此实际上在绝大多数深度范围内几乎没有额外的量化误差。
- 在许多情况下,分离视图矩阵和投影矩阵(遵循 Upchurch 和 Desbrun 的建议)确实会带来一些改进。虽然这并没有降低总体错误率,但它似乎确实将互换变成了无法区分的东西,这是朝着正确方向迈出的一步。
- 一个无限远的平面在错误率上的差别很小。 Upchurch 和 Desbrun 预测绝对numerical误差会减少 25% ,但这似乎并没有转化为comparison误差率的降低。
不过,以上几点实际上并不重要,因为这里真正重要的结果是:反向 Z 映射基本上是神奇的。过来看:
- 在本测试中,带浮动深度缓冲器的反向 -Z 给出零错误率。现在,如果您继续收紧输入深度值的间距,当然可以使其产生一些错误。不过,与其他任何选项相比,带浮点数的反向 Z 更精确,令人可笑。
- 带整数深度缓冲区的反向 -Z 与任何其他整数选项一样好。
- 反向 Z 消除了预合成与单独视图/投影矩阵以及有限与无限远平面之间的区别。换句话说,使用 reversed-Z ,您可以将投影矩阵与其他矩阵组合,并且可以使用您喜欢的远平面,而不会影响精度。
我认为这里的结论是明确的。在任何透视投影情况下,只需使用带反转 Z 的浮点深度缓冲区!如果不能使用浮点深度缓冲区,则仍应使用 reversed-Z 。它不是解决所有精度问题的灵丹妙药,尤其是在构建包含极端深度范围的开放环境时。但这是一个很好的开始。