在科学和工程领域，模拟已经被广泛用于模拟各种现实问题。人工智能和机器学习的最新发展已经导致使用数据来构建模拟的替代物，但最新的努力集中在将科学定律注入神经网络上。
NVIDIA SimNet 是一个基于物理信息神经网络（ PINN ）的人工智能工具包，可用于解决正向、反向和数据同化问题。希望通过实际应用解决复杂非线性物理问题的工程师、科学家、学生和研究人员可以通过使用 AI 驱动的物理模拟从 SimNet 中获益。
SimNet 今天应用的一个成功案例是制造和环境空气控制系统设计优化的自动化。这些使产品设计师能够在没有大量领域专业知识的情况下调查任何给定设计的性能。此应用程序使用物理信息神经网络（ PINNs ）将 2D 喷嘴流的详细流体动力学解决方案与商业 CAD 软件耦合。这项工作由迈克尔·艾德尔（ Michael Eidell ）领导，他是 Kinetic Vision 建模与仿真小组的高级工程师。 Kinetic Vision 是一家位于辛辛那提的科技公司，为《财富》 500 强提供服务。他专注于快速为客户找到见解，并以令人信服的方式传达这些发现，以帮助客户通过高效的概念到生产解决方案满足其复杂的产品和系统开发需求。
Michael 的团队在 SimNet 和传统计算物理工具之间观察到的主要区别因素是，它不依赖网格来离散域，其几何模块提供了构建参数化特征的灵活性，例如，边半径。代码在多个 GPU 上的可伸缩性是 Kinetic Vision 团队成功证明 SimNet 是可行的产品设计工具的另一个因素。
基于仿真的产品设计与优化
作为一家拥有大型产品设计团队的公司， Kinetic Vision 的工程师通常会对设计性能进行详细的计算物理评估（例如， FEA 、 CFD ）。这通常包括执行多个设计迭代、生成各种计算网格以及运行第一原理解算器。当考虑到大量的设计变量时，与此过程相关的运行时间和劳动力可能会非常昂贵且时间密集。在某些情况下，可以适当降低模型保真度。但对于涉及复杂流体动力学的问题，必须考虑完整的 Navier-Stokes 方程。
Michael 和他的团队之前曾探索过使用其他商业溶剂来开发 2D 喷嘴的简单流体模型。然而，由于多种因素，他们决定使用 SimNet 平台：
- 该团队在机器学习领域使用 GPU 的经验非常丰富。
- 公司内部强烈希望探索 GPU 在基于物理的建模中的使用，以帮助加快产品设计过程以及建模和仿真工作。
- SimNet API 是基于 Python 的，这使得采用和开始对真实世界问题进行原型设计变得更加容易。
SimNet 完全符合团队的经验和发展目标。
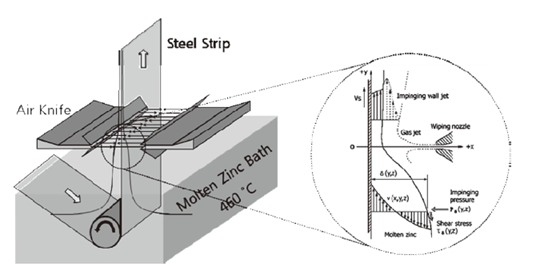
Michael 的团队开始建立一个 3D 气刀系统的 2D 模型，模拟镀锌过程中使用的热气擦拭系统。气刀是一种亚音速气体喷嘴，它将气体排放到附近的钢带上，钢带已浸没在熔融锌中。这种气体有助于保持钢带上锌的厚度一致，从而对钢进行镀锌（图 1 ）。
SimNet 入门
使用 SimNet 的几何模块，将亚音速气体喷嘴建模为入口、实心壁和压力出口，以模拟周围环境（图 2 ）。
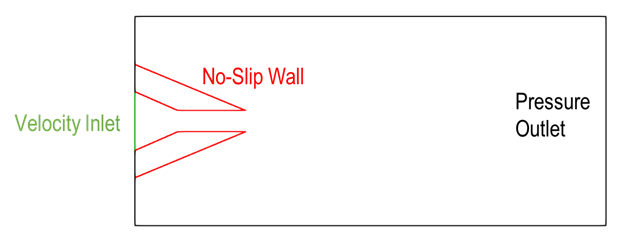
SimNet 中采用的无网格方法仍然需要对感兴趣的领域进行适当采样，以帮助捕获所有显著的流动特征。设置问题后，可以使用工具（如 Paraview ）可视化几何图形。
图 3 比较了 2D 喷嘴问题中可采用的两种不同批量取样方法。上部图像显示均匀采样，而下部图像包括射流潜在核心中的高分辨率区域，其中可能出现一些最大的速度梯度。
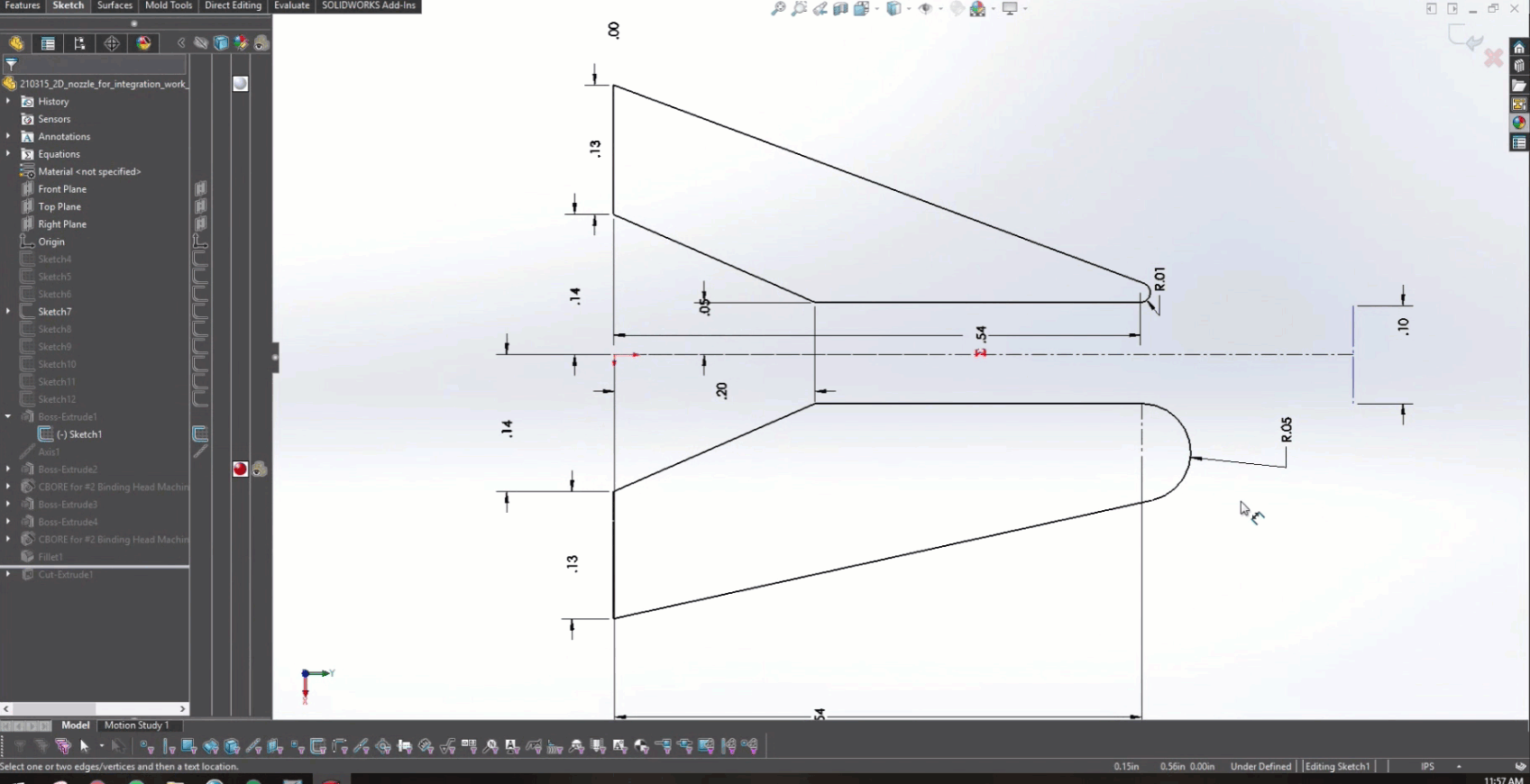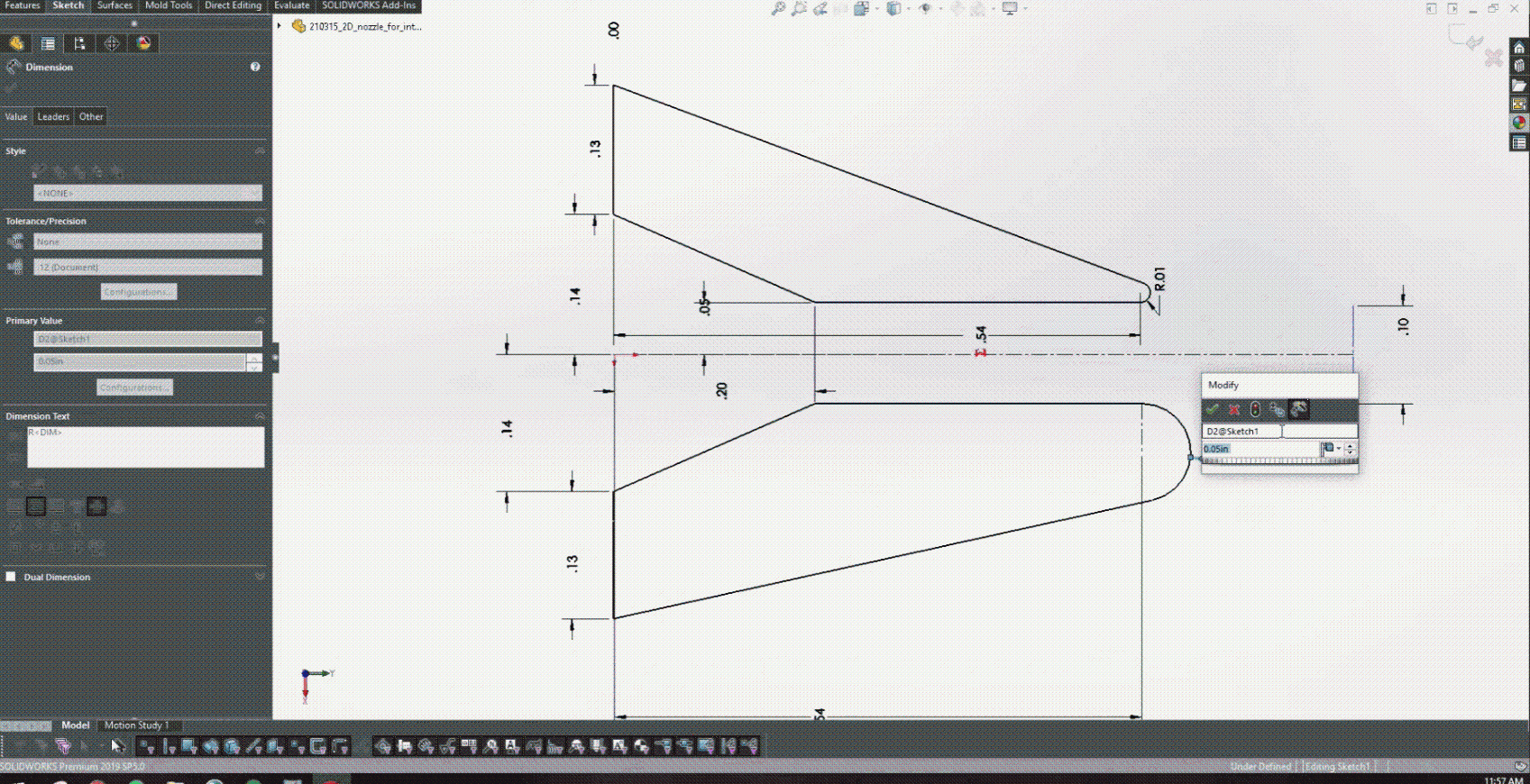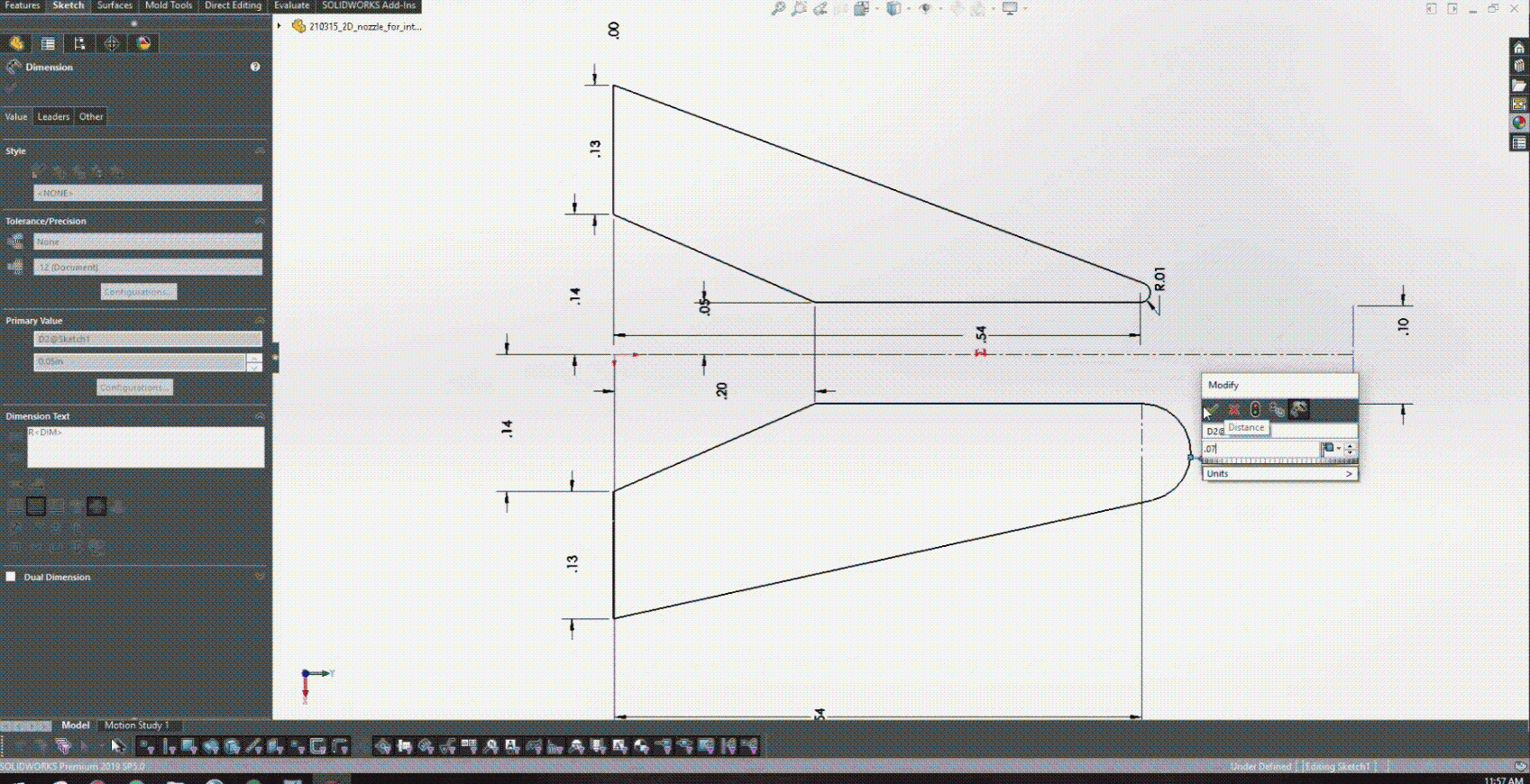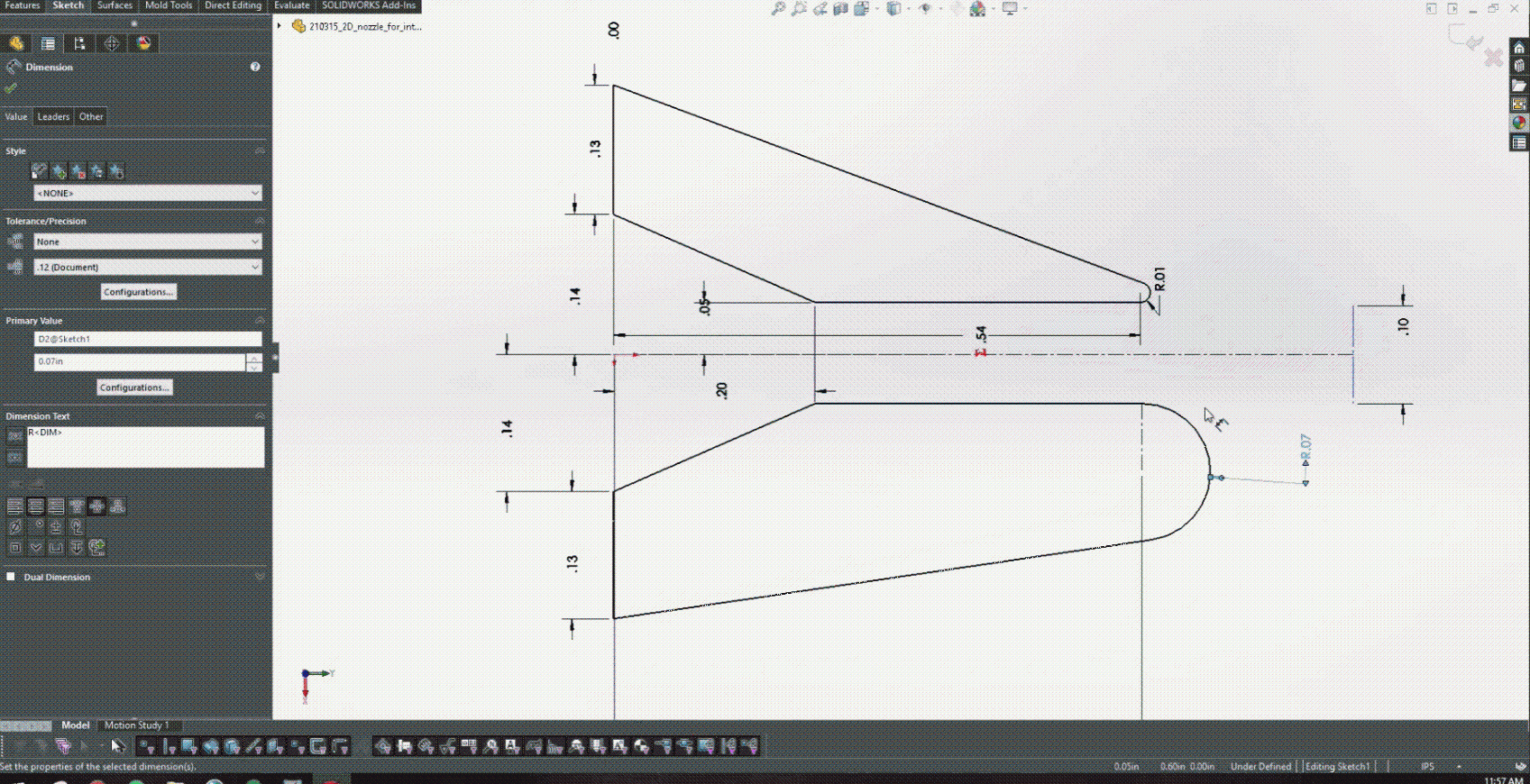
探索科恩达效应作为一种控制射流角度的方法，是这一问题的研究重点。 Michael 的团队通过在喷嘴后缘添加半径来探索这一点。喷嘴的上后缘具有固定半径，而喷嘴的下后缘具有变化。图 4 显示了在下后缘上探索的一些离散半径值的简单描述。
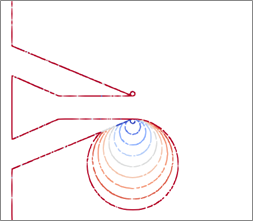
最终培训的 PINN 与 Solidworks 结合，以帮助演示产品设计师如何在设计气刀时使用培训过的模型。简单矩形气刀的 CAD 模型是在考虑现有产品的情况下生成的。
设计优化运行
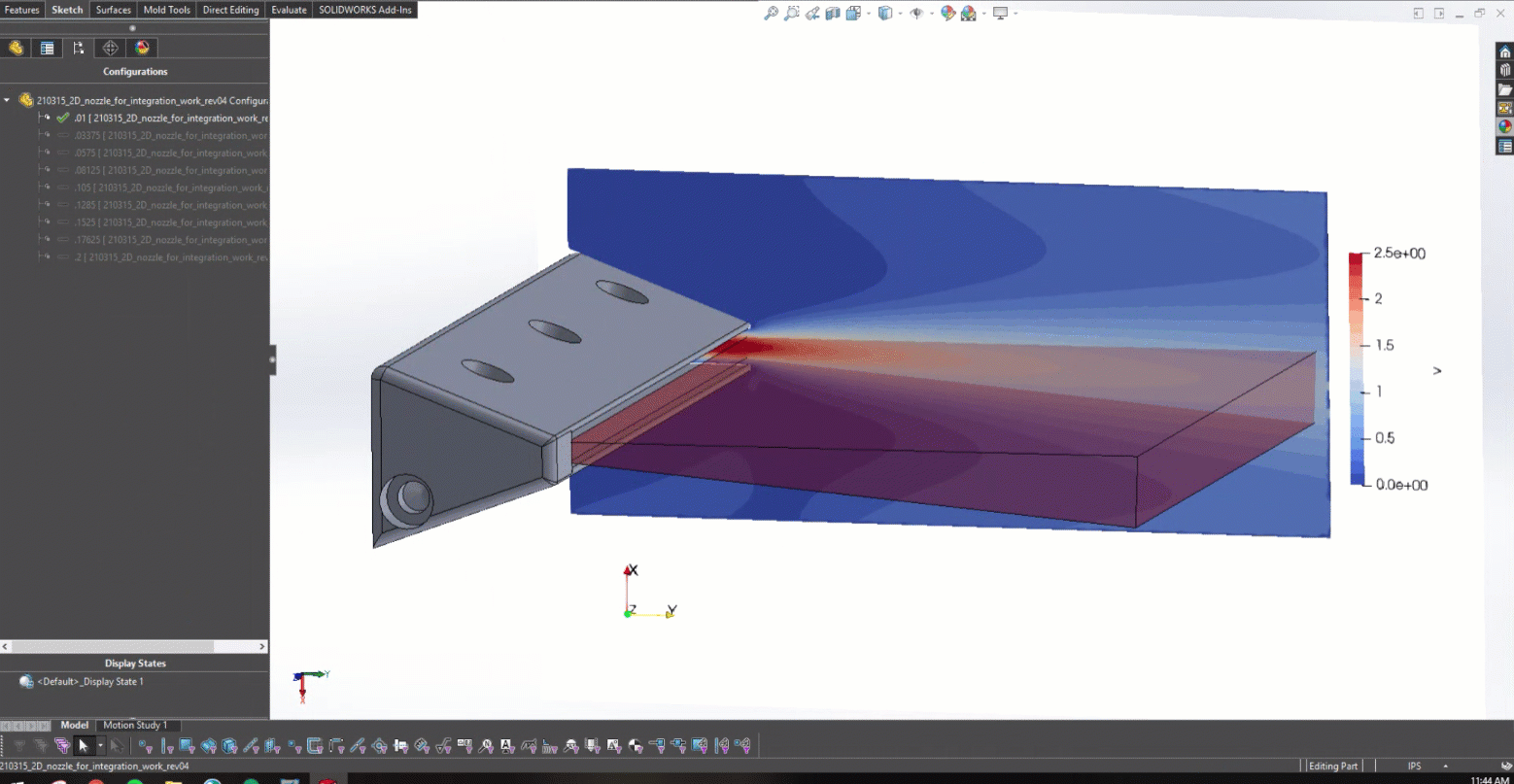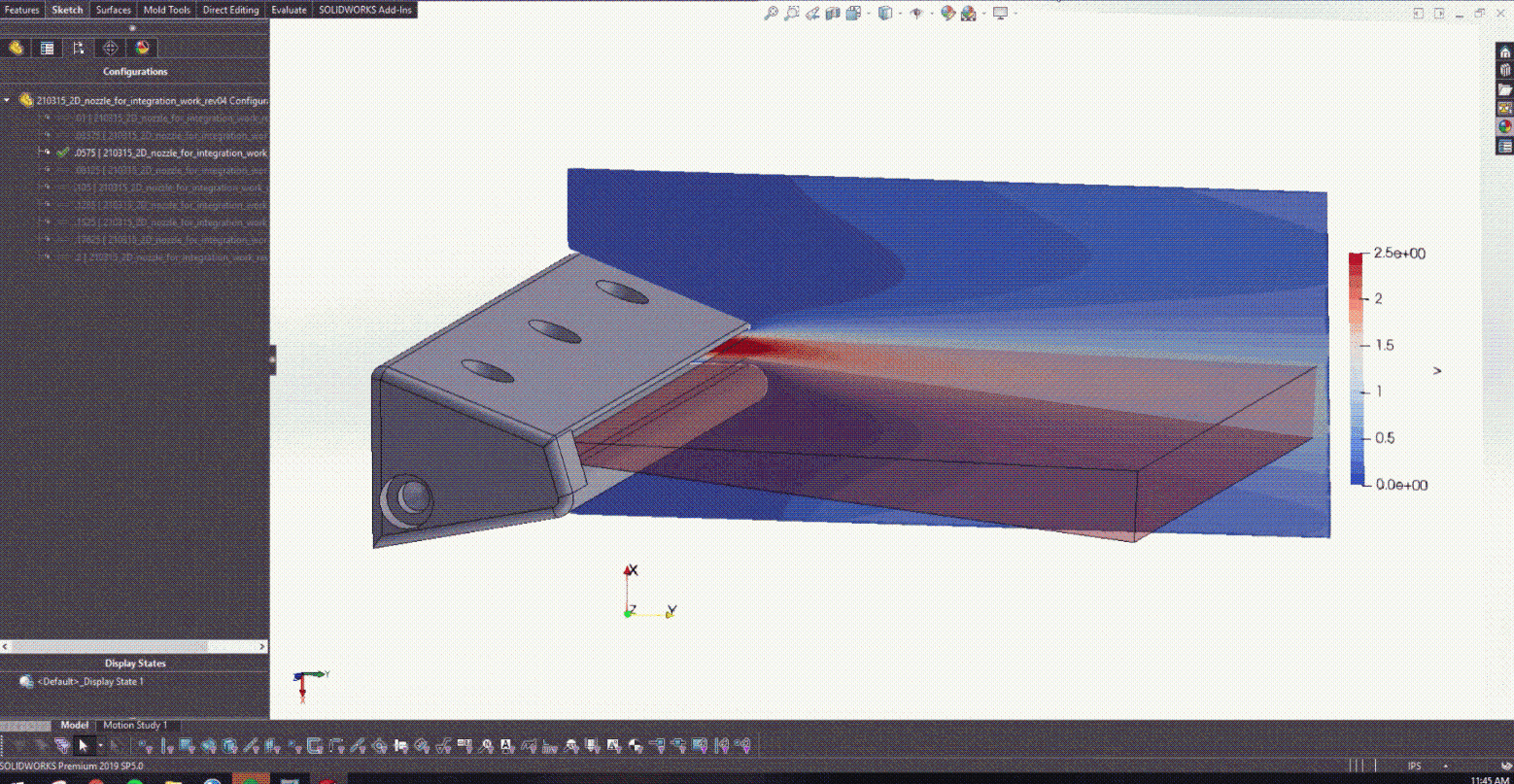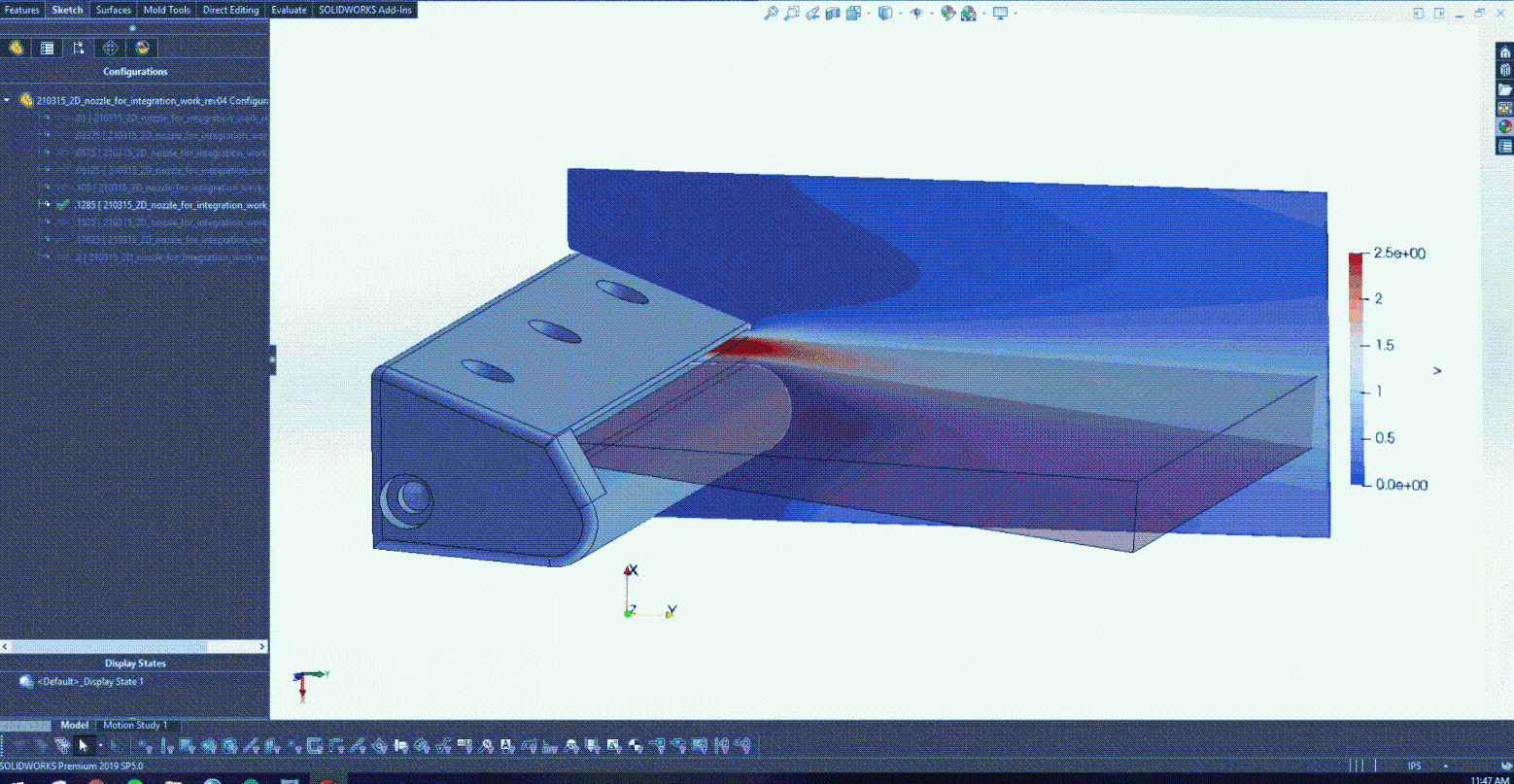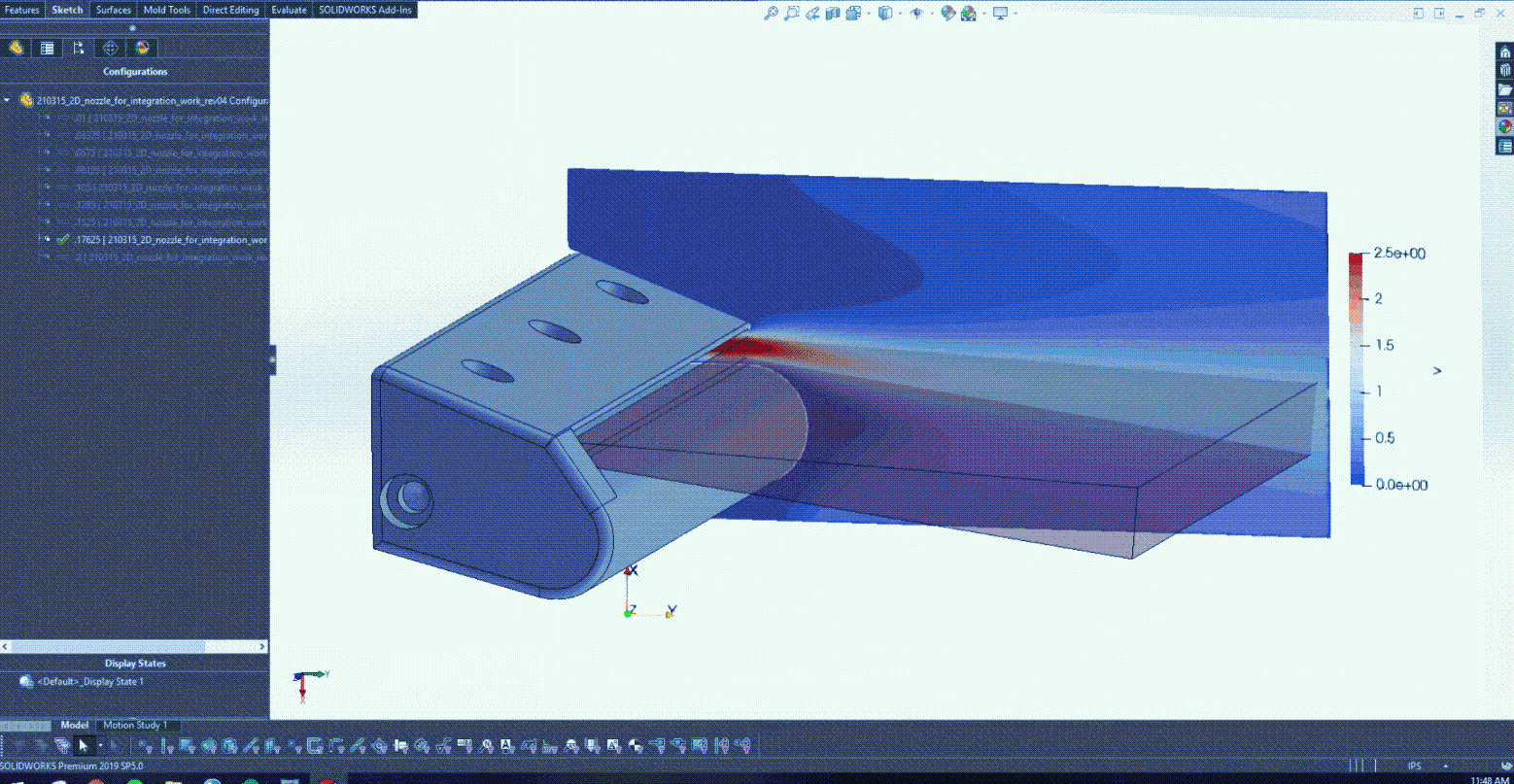
在图 5 中培训了 PINN 并开发了 CAD 模型之后，就可以开始与 Solidworks 进行耦合了。图 6 实际显示了改变较低的后缘半径如何为设计提供实时反馈，以确定产生的射流角度。
在这项工作中，气体擦拭过程的物理简化为二维等温层流射流。控制此类层流射流的方程式如下：
\begin{equation} \label{eq:1}
\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0
\end{equation}
\begin{equation} \label{eq:2}
u \frac{\partial u}{\partial x} + v \frac{\partial v}{\partial y} = \nu \frac{\partial^2 u}{\partial y^2}
\end{equation}
方程 1 和 2 分别是二维层流射流的质量守恒和动量守恒，其中
方程 1 和 2 的解可通过产生以下形式解的相似技术进行：
\begin{equation} \label{eq:3}
u = \left(\frac{3M^2}{32\rho^2\nu x}\right)^{1/3}\sech^2\left[y\left(\frac{M}{48\rho\nu^2x^2}\right)^{1/3}\right]
\end{equation}
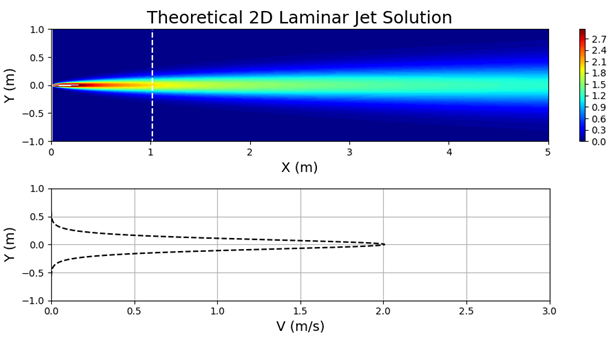
图 7 显示了为指定值绘制的方程式 3
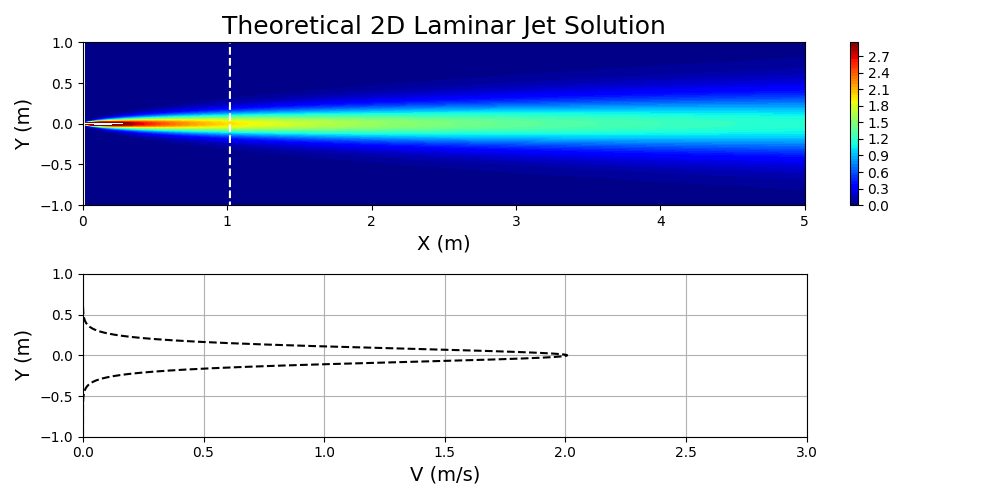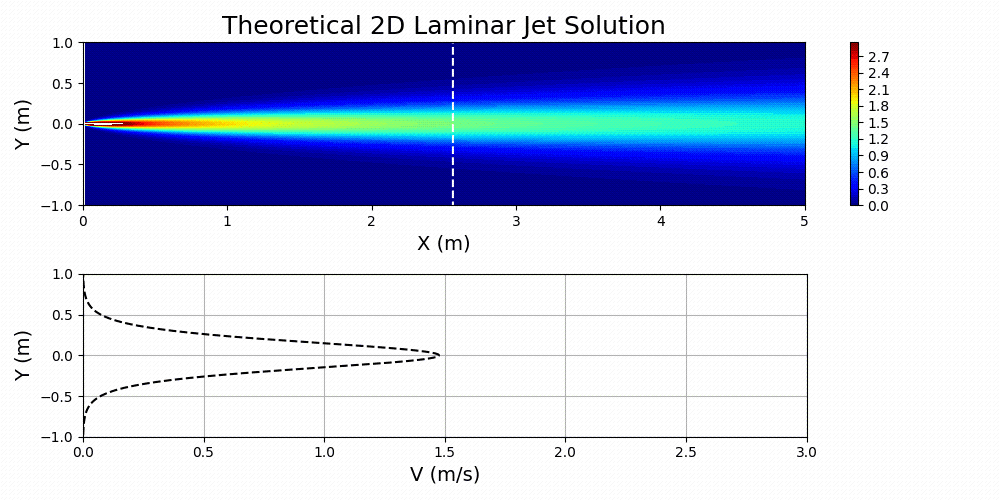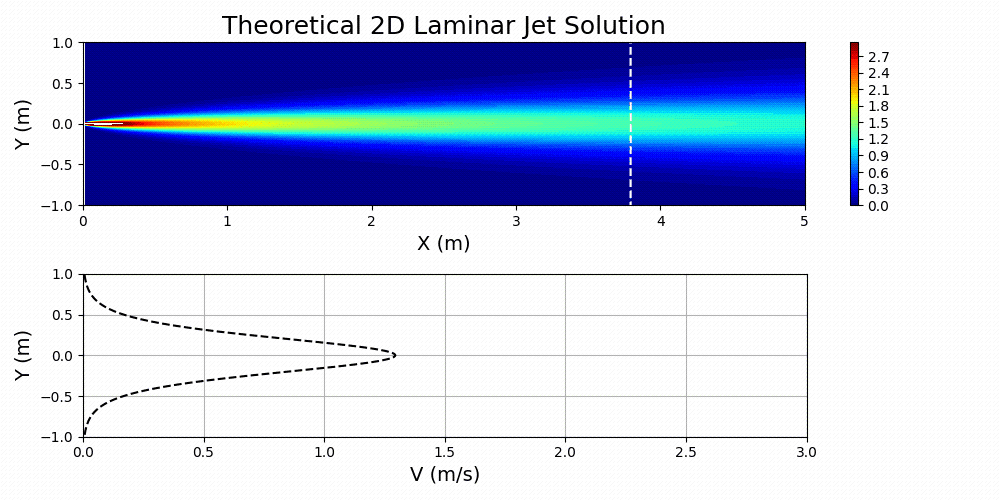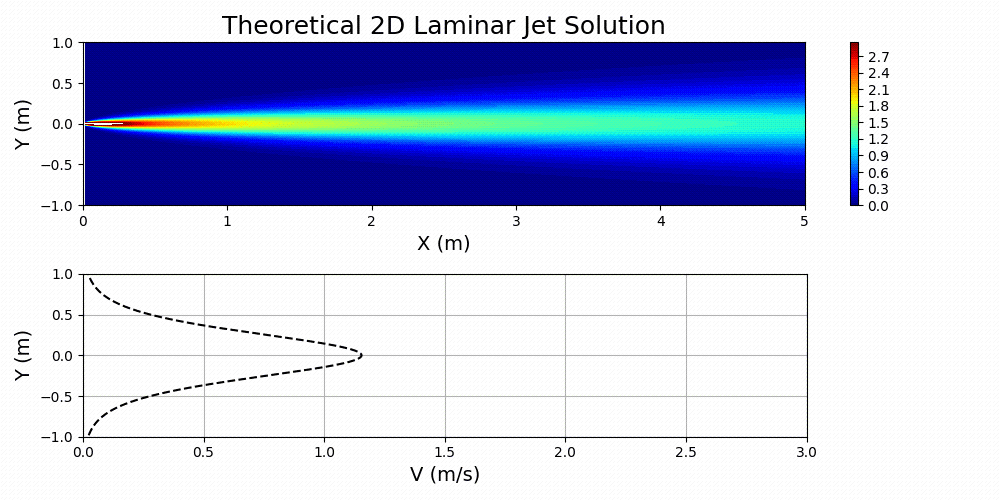
对这个问题感兴趣的流体被认为是空气。通过首先计算问题所需的雷诺数，然后基于已归一化的域求解有效运动粘度，在主 SimNet 输入文件中指定流体的特性。本质上，物理域和归一化域之间的动态相似性是通过雷诺数匹配实现的：
\begin{equation} \label{eq:4}
Re = \frac{UD}{\nu} = \frac{\tilde{U}\tilde{D}}{\tilde{\nu}}
\end{equation}
使用方程式 4 ，可以指定物理速度
在该区域的入口处，指定了抛物线速度剖面，以防止无滑移条件紧邻指定入口速度的墙壁附近出现任何不必要的数值刚度。因此，需要一个抛物线剖面，当它接近墙壁时，速度达到 0 （图 8 ）。
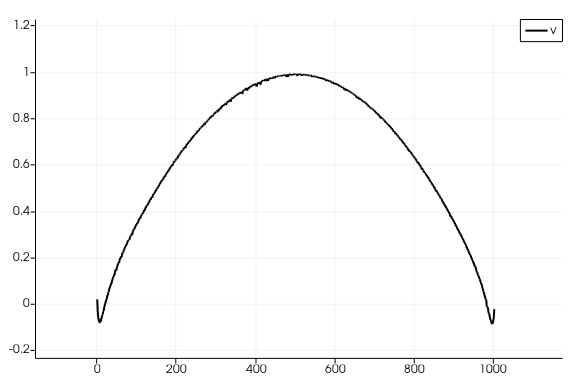
训练该模型所采用的数值方法是使用自适应矩估计（ Adam ）优化器，并依赖于改进的傅里叶结构。根据 SimNet 文档中提供的指导，并通过与 NVIDIA SimNet 开发人员的合作，选择了改进的傅立叶体系结构。
一般来说，一组守恒定律可以写成如下：
\begin{equation} \label{eq:5}
u_t + \mathcal{N}[u] = 0, x \in \Omega, t \in [0,T]
\end{equation}
在这里
\begin{equation} \label{eq:6}
L_{residual} = \frac{1}{N_u}\sum_{i=1}^{N_u}|u(t_u^i,x_u^i)-u^i|^2 + \frac{1}{N_f}\sum_{i=1}^{N_f}|f(t_f^i,x_f^i)|^2
\end{equation}
图 9 显示了本工作中讨论的 2D 喷嘴问题的最小化该残余的结果。通过运行 TensorBoard ， SimNet 情况下很容易生成这种类型的损失函数残差图。有关此工具的更多信息，请参阅SimNet 用户指南.
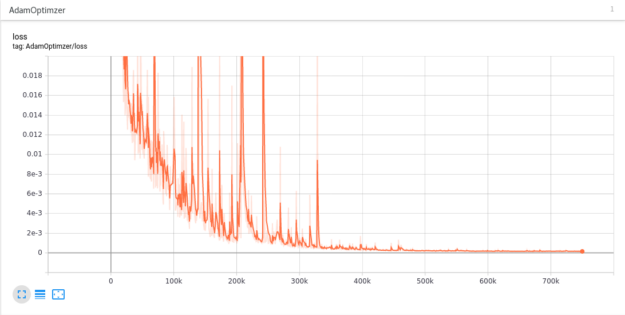
图 10 显示了本研究中探索的半径子集的速度分布结果。该动画捕捉了 SimNet 作为探索性设计工具的强大功能，可用于在大型设计空间中同时训练钉。
结论
Michael 的应用程序目前是用 Python 编写的概念验证，并使用其内部 GPU 集群（ NVIDIA V100 和 NVIDIA A100 ）在一个、四个和八个 GPU 上运行。
Michael 的团队在 SimNet 和传统计算物理工具之间观察到的主要区别因素是，它不依赖网格来离散域，其几何模块提供了构建参数化特征的灵活性，例如边半径。代码在多个 GPU 上的可伸缩性是 Kinetic Vision 团队成功证明 SimNet 是可行的产品设计工具的另一个因素。
Michael 进一步阐述了他在 SimNet 方面的经验：
“ SimNet 代表了模拟某些类别问题的范例变化。可扩展计算可用于探索复杂问题的整个设计空间，节省数百小时的交互式工程时间以找到最佳结果。我们有许多客户对物理建模、机器学习和 SimNet i 感兴趣现在，我们已经将其列入了应对《财富》 500 强制造业挑战的技术清单。”
有关更多信息，请参阅利用物理信息神经网络和 SimNet 加速产品开发GTC 会议。有关功能和下载工具包的更多信息，请参阅英伟达 SimNet产品页面。
