Analysing Stutter – Mining More from Percentiles
Stutter and hitching are often talked about when comparing games or measuring performance. However subjective comparisons are not that useful during development. In this article I will show an approach that can be used to quantify frame rate using statistical analysis. This allows for an objective comparison of performance during development. By measuring stutter and reducing it over time you can ensure your game delivers a smooth experience for the gamer.
Although stutter in games has always been a problem, my own approach to measuring and fixing stutter changed completely, back in 2011, when The Tech Report’s Inside the Second article introduced me to percentiles. Thank you, Scott Wasson! Since then, the use of frame-time percentiles has grown and spread within NVIDIA. We now have a tool to help compute percentiles and we measure stuttering as a matter of course when testing new games.
Percentiles are not the only way to measure stutter and debate has raged many times, here at NVIDIA, about the best approach. But I consistently find that percentiles are easy to measure; they have an intuitive interpretation; they can be used to quantitatively compare different results; and – perhaps most importantly – they always match my subjective game-play experience.
What does a percentile mean when applied to frame times? The Tech Report has plenty of great discussion and examples. But briefly, for a given percentage, say 99%, a percentile of 35.6ms means that 99% of the frame times fall below 35.6 ms. Long frames matter for stutter analysis and so I often think of the percentile meaning the other way around: 1% of values are 35.6 ms or above.
What do I mean that percentiles have an intuitive interpretation? At its most basic, if you plot a sequence of percentiles, a stuttering game has a distinctive, hockey-stick shape – like a curved L. A better-behaved game has a flatter curve. The graph below is a real example from NVIDIA testing during the beta of a well-known 3rd person shooter. I’ll call it Game A. The two curves are quite different. Clearly, we had a problem here on card X compared with the other card Y.

There is more that can be read from the graph shapes. Stutter frames come in a variety of distributions. Here is the time-per-frame graph corresponding to the yellow percentile line above. It stutters often and at a wide variety of different frame durations – everything from 30ms up to 120ms.

At another extreme, a game can be super smooth for 99.9% of the time but hitch badly for a tiny minority of frames. For Game A again, here is a frame-time plot for a different level, with different CPU hardware:

Clearly, there is still a stuttering problem but it is far less frequent. The percentile plot has a different, distinctive shape - the graph tends to square off, becoming less curved:

The red data set illustrates an interesting point about x-axis values. The red percentile graph uses a different set of x-axis percentage values. The top three percentage values for the blue and yellow graphs are 99, 99.5 and 99.8. If you stop at 99.8 for the red graph, the highest y value is 15.9ms and it looks only slightly worse than the blue plot, hiding the problem with the small number of stutter frames. To see the L-shape, we need to additionally examine the values at 99.9 and 99.95%. By contrast, the blue and yellow graphs get interesting at lower percentages - about 98 to 99.5%. Different curves are useful at different x-axis ranges.
You can compute percentiles at very tightly spaced samples (and our tool supports this – below). A sample spacing of 0.05 is required to show the L-shape of Game A’s red data set. This works just fine but there tends to be no interesting, useful detail below the mid-90s and you get lots of values that are uninteresting.

Hence, I find it most useful to examine a range of x values that asymptotically approach 100%. A curve is summarized by about 10 manageable values but still shows the detail where you need it. The above L-shaped, red curve uses x values of 99.0, 99.5, 99.8, 99.9 and 99.95. These were somewhat arbitrarily chosen by hand. I have since settled on a formula of 100-2n, where n is both positive and negative. This is implemented by the “exponential” mode of our tool below.
However, beware of very closely-spaced percentage values – close to 100 – applied to small data sets. If you have “only” 2000 frame times, the 99.95th percentile represents only a single value in the input data. The result is still valid and a single bad stutter frame still matters deeply to the subjective game-play experience. But with small data sets, the ultra-high percentiles will probably be noisy because stutter tends to be random. Yet reliable comparisons between runs are essential for problem triage and regression testing, etc. To make the ultra-high percentiles repeatable, Game A’s yellow data set has 41000 frame times and red has 19000. (We did lots of testing.) The maximum percentage on the next graph below is 99.94% which represents 25 frame times for yellow, 11 for red but only 1 for purple. Our tool produces a warning if a percentile is represented by very few frame times.
All my plots here also avoid 100%. The 100th percentile is, by definition, the maximum value and can only ever be represented by a single frame (and the 0th is the minimum). So I tend to avoid the 100th percentile for the same reasons of repeatability between runs. Likewise, the exponential mode of the tool doesn’t emit 100%; its default maximum is 99.87%.
It is easy to distinguish Game A’s red frame-time graph from the yellow because I chose the red data set as an extreme example. Subtle differences between data sets can be more difficult to eyeball from frame-time graphs. Nor does eyeballing the frame-time graph give you a quantitative measure of stutter.
Here’s a frame-time plot from another, recent AAA game. Call it Game B.

Game B obviously stutters heavily. The frame-time graph looks to my eyeball as though it stutters less than the yellow Game A plot above. But subjectively, it stutters more. And this is borne out by a variety of different analyses: frame counts above a threshold and the standard deviation are all higher for the purple data than for the yellow (details in the spreadsheet here). So the frame-time graphs seem misleading to me.
However, the percentile graph tells an immediately obvious story. The purple percentile line starts to slope up quite rapidly in the mid-90% range. The interpretation is that many values are well above average. For example, the 96th percentile value is +20ms, meaning that 4% of frame times were at least 20ms above average. This app is stuttering often.

Eyeballing the above frame-time graphs does not work well because each shows widely different numbers of samples. The yellow data set contains 41k values, the red is about 19k but the purple has only 1800 values. If I replot 1800 representative frame-times from each data set, they start to correlate better with the percentiles and other analyses:



Note that the last percentile plot above is slightly different from the preceding ones. When comparing graphs from different hardware, levels or games, the average frame-times can vary widely, the curves are separated, and it can be slightly difficult to eyeball the resulting slopes. Here, the curves are normalized. For each data set, the benchmark average frame time has been subtracted from all percentiles. The normalized curves then all slope upwards from zero, highlighting the differences in slope.
And this is the essence of what we want to look for in a percentile graph: how quickly does it start to slope upwards? The percentile plots have an obvious and intuitive interpretation that relates back to the raw frame-time data. Other measures are shown in the spreadsheet but to my mind, they lack that intuitive interpretation. All these examples can be correctly ranked by standard deviation – which is somewhat useful if you want a single-number summary per data set. The purple data set has a standard deviation of 10.01ms. But what does that mean? The percentile definition, “4% of frame times were at least 20ms above average” is much more useful to me.
For normalization, my first instinct was to divide all percentile values by the average for the run. To my slight surprise, this made all the curves too similar and difficult to distinguish. A simple thought experiment suggests that dividing by the average is less useful:
- Game X runs very fast, averaging 5ms per frame. Stutter frames of 3x average = 15ms might be subjectively tolerable (especially if v-sync is on).
- Game Y runs slowly, averaging 30ms per frame. Stutter frames of 3x average = 90ms would definitely be subjectively poor.
The ratio of stutter/average is 3 for both cases and does not usefully indicate that Game Y is worse. Absolute values matter more when measuring frame time.
Interestingly, our purple curve for Game B also slopes down more rapidly towards zero percent:

The interpretation is that there are more frames that are well below the average. For example, the second left-most data point shows that 2% of frames were 15ms below average. Again, Game A is flatter. Zooming into Game B’s frame-time plot shows the reason.

Long, hitch frames are often followed by exceptionally fast frames. This is typical of a deeply pipelined system with concurrency. It simply means that one part of the system has managed to become totally idle during the long hitch and so the next frame runs faster. It's interesting but it's not clear that exceptionally small frame times are useful for stutter analysis. It’s the long frames that you notice subjectively. And so we don’t usually measure percentiles down to zero. I think this is fine.
Nth percentile is a standard function in Microsoft Excel. Even so, a number of steps are required to go from Fraps’ raw frame-time data to a sequence of percentiles that you can graph. I like to think that my Excel skills and shortcuts are pretty slick but it still takes me 20 or 30 seconds to produce a graph from a Fraps log file using Excel alone and that’s using a pre-existing template with all the formulae. So we wrote a simple tool – fraps2percentile – that computes a range of percentile values based on the output of Fraps. With one command, fraps2percentile will compute multiple percentiles for multiple sets of data. It’s pretty simple and the full source code is included below.
A couple of the ideas discussed above are directly supported by options in the tool: the -exp command line option will create exponential x values; the -nor option will normalize the y values by subtracting the average frame-time. The final percentile graph above was produced with both these options. (However, the graph that highlights the negative y values is a manual composite. The tool doesn’t support x values that decrease towards zero. It is easy to produce similar graphs by using a small bin width over the range 0 to 100.)
Armed with the tool (or a spreadsheet), we constantly compute percentiles when testing games. What’s more, a few years of experience has led to high confidence in the results. We trust the numbers and graphs. When testing Game B, we noticed a repeatable slight difference between drivers. Importantly, the difference in subjective experience was not noticeable because the subjective experience is overwhelmingly poor in either case, masking the driver’s contribution. But if the numbers say that one driver is subtly worse, that is enough evidence to suspect a driver regression and we investigated further.
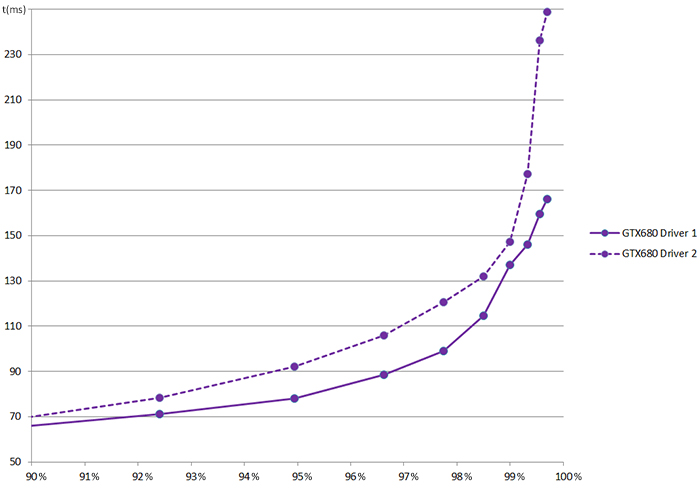
Also, if our test lab produces a flat percentile graph for the latest game, I believe that the subjective experience was good. Returning to the original example, of Game A, we worked with the developer to debug and fix the game (the problem wasn’t in the NVIDIA driver). The resulting graph shows a clear difference between the two releases of Game A and game-play was far better at the time of release due to the use of percentiles during beta testing.

References
Around this time, The Tech Report starts plotting graphs of percentiles:
Example Data
For readers who care about the details, I think it may be useful to see how all my graphs and numbers were derived. This file contains five sets of raw data for Game A and Game B. It shows how to compute percentiles using only Excel, without our fraps2percentile tool. It also shows a couple of other stutter measures: stdev and counts above a threshold, where thresholds are average+n. And finally, it shows the frame-time graphs. (There are seven worksheets – don’t miss them all.) This file contains the original raw data files in case you wish to reproduce my numbers.
In the latter percentile plots, I switch to showing the output of fraps2percentile -exp -nor. The raw input data is the same five sets in the first spreadsheet. The tool output is shown here. The composite percentile plot that includes the values down to 0% is shown on a second worksheet.
fraps2percentile tool
The source code for our tool is provided here. We compile it with Visual Studio 2010 although the trivial project files are not included here for simplicity.
Caveats
- A couple of the most recent features were added while writing this article and haven’t been widely tested, namely the small-percentile-bin warnings and the normalization mode.
- The command line processing isn’t the most robust and it is possible to break it. I would use a robust off-the-shelf lib – I’m a fan of boost. But I am trying to keep the tool self-contained and simple so that you can compile it easily, without fetching other libs.
- There is an inconsistent mix of stdio and iostreams. Apologies for the poor style, but it works.
- The tool accepts input data written by Fraps frame time logging. Supporting other data sources would be useful. But again, I am keeping the source simple here. Feel free to extend it.